 |
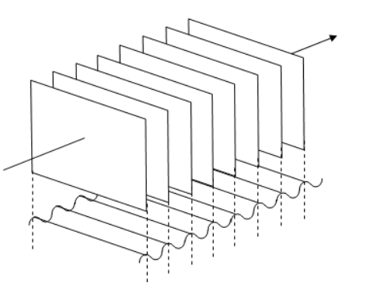
| 図1 平面波イメージ |
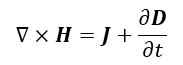 | (1) |
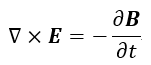 | (2) |
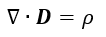 | (3) |
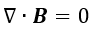 | (4) |
| 率、透磁率はそれぞれ真空中の値(便宜的とされているもの) | 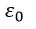 、 、 | 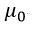 | を用いると |
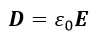 | (5) |
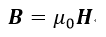 | (6) |
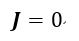 | (7) |
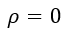 | (8) |
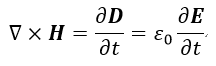 | (9) |
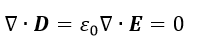 | (10) |
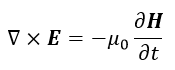 | (11) |
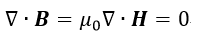 | (12) |
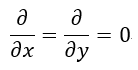 | (13) |
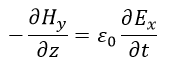 | (14) |
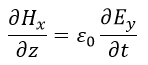 | (15) |
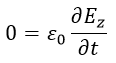 | (16) |
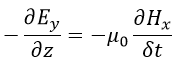 | (17) |
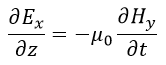 | (18) |
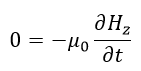 | (19) |
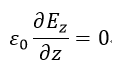 | (20) |
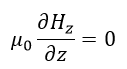 | (21) |
| (16)、(19)~(21)より、 | 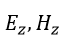 | は時間的にも空間的にも変化しないことになります。 |
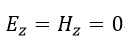 | (22) |
| 求める対象は、 | 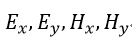 | の四つであり、四つの方程式(14)、(15)、(17)、(18)を解けば |
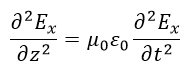 | (23) |
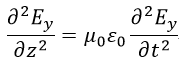 | (24) |
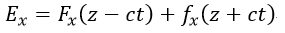 | (25) |
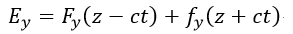 | (26) |
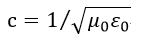 | (27) |
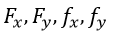 | :任意の関数 |
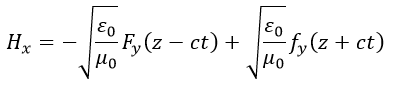 | (28) |
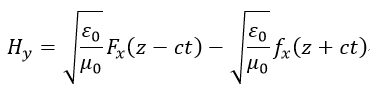 | (29) |
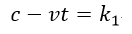 | (任意の定数) |
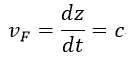 | (30) |
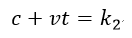 | (任意の定数) |
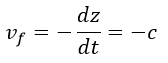 | (31) |
| 例えば、 | 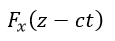 | の関数に対して電界、磁界は図2となります。 |
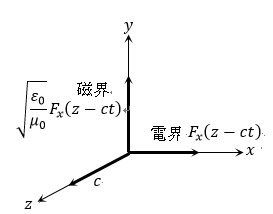 |
| 図2 |
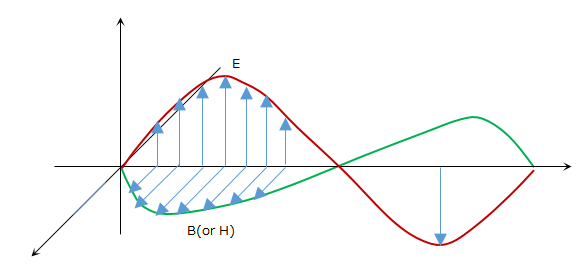 |
| 図3 |
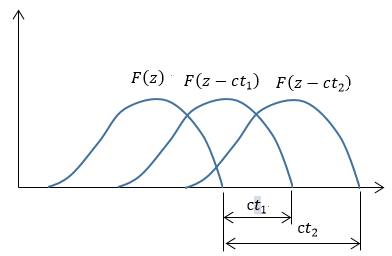 |
| 図4 zの正方向に進む進行 |
| 私の素朴な疑問は、周波数があるなら、 | 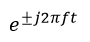 | という項があるのではないか? |
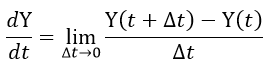 | (32) |
| であり、決して | 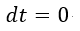 | ではないのです。 |
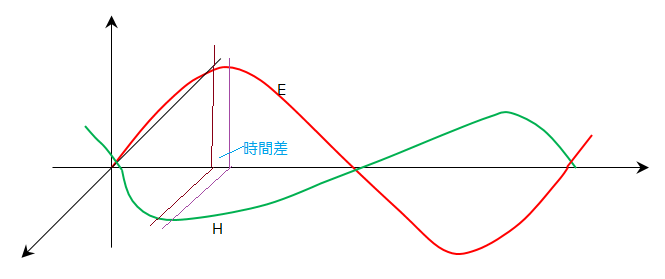 |
| 図5 |
| 時間がt→t+dtの間の | 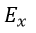 | の時間的変化勾配がz→z+dzの間の | 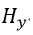 | の空間的変化勾配に等しい |
| 時間がt→t+dtの間の | 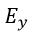 | の時間的変化勾配がz→z+dzの間の | 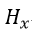 | の空間的変化勾配に等しい |
| 時間がt→t+dtの間の | 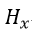 | の時間的変化勾配がz→z+dzの間の | 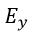 | の空間的変化勾配に等しい |
| 時間がt→t+dtの間の | 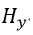 | の時間的変化勾配がz→z+dzの間の | 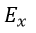 | の空間的変化勾配に等しい |
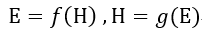 | でも | 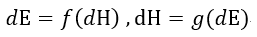 | でもないのです。 |
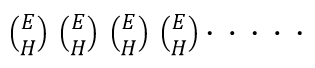 |
| 図6 |
|
と言う形で E,H(B)両者の波が同時進行していく(※5) と考えています。 これについては、ネット検索しましたら、EMANさんの「EMANの電磁気学」の中でも、それまで 一般的に語られ自分もそう説明してきたとしてよくある「水平の環と垂直の環を鎖状に繋げた」図 を示され、しかし検討された結果として私の考えている(※5)と同様な結論を赤字で示されておら れましたので私一人の思い込みではないと思っています。 ただ、②のような説明が本においてもなされているそうですから、そういう説明がされるにはそれ 相応の根拠があるだろと考え、その根拠について考えてみました。「マックスウェルの方程式」か らは私は前述のような解釈しかできないため他の理由を考えてみました。 私が思いつきましたのは、Faradayが発見した「電磁誘導(電流→磁気)」「磁電誘導(磁気→電流)」 の二つでした。そして「帯電」と「電荷」も考慮してみました。 まず、「帯電」というのは電気を帯びた状態で、電磁気学において、「電荷」というものの存在でそ れが説明されています。そして静止電荷(電荷量をqとします)でもその周囲に
今、「電流」というのを考えますと、これは「電子の流れ(移動)」で説明されていて、電子というの はその1個の持つ電荷量は1.6×10^(-16)[c]となりますので、電荷と結びついています。それゆえ 電荷というものに還元でき、電流は電荷の流れとみなすことができます。 実際、導体内に電流が流れるときの電流値は流れる電荷量をQとしますと、
一方、磁界(磁場)H(B)は「電流が流れる」ことにより発生します(電磁誘導の法則)。 したがって、一番最初の段階、すなわち電磁波源が励起された途端を考えたとき、 まず帯電で「電荷」を持ち、周囲に電界(電場)ができる→電流が流れ始めると 磁界(磁場)ができる と考えた時、最初の時点では、経時的に「E H 」(または「E B」)となると考えられなくはありま せん。しかしながら、これからは、「E→H 」(または「E→B」)というメカニズムは出てこないと思うの です。「電磁誘導」「磁電誘導」はあくまで、電流とH(B)との間の物理的現象です(後者はH(B)と回 路との相対的値変化でも発生しますが)。EとH(B)の関係ではありません。 したがって、これからは「E→H(B) 」「H(B)→E」という関係、そして、「E H(B) E H(B) ・・・」という経 時的流れが出てくる理由が私にはわかりませんでした。 結局、考えてもどうもよくわからなかったのですが、大変失礼な解釈ですけど、上記の考察と、(9) 式では左辺にHがあり、右辺にEがある、(11)式では左辺にEがあり、右辺にHがあることを考え 併せてそういう解釈がなされたのではないかとも思っています。しかし、それについて私は式から はE→H(B)、H(B)→Eというのは出てこないことを前述で示しました。 以上、本などで示されて来た物理イメージの否定であり、勿論、自分の浅学菲才は重々承知し ていますし、十分ご理解されていらっしゃる方からの反論はあるとは存じますが、とにかく電磁気 学を再勉強した中での私の結論は以上です。 ただ、私はこういう解釈が生まれたそもそもの要因は、(1),(2)式を根本的に解釈誤りでいている からではないかと思います。私は、(1)、(2)式と言うのは、「右辺の結果が左辺」ではなく、「右辺 の結果と左辺の結果が等しい」ことを示している式である思います。これらを明確に分けている C言語で云いますと等号「=」はC言語における「=」ではなく、同じくC言語における「==」に相 当するものと考えています。そう考える理由は後述します。 さて、前述の(※3)についてですが、私の所有する教科書に、「電磁波の放射」という章があり、 冒頭で「この問題は本質的には電磁波の動きを表現している波動方程式の励振の問題 である」と書かれていて気が付いたのでした。 確かに「電磁波」は「波の伝搬」であり、抽象的な電磁波理論ではなく、具体的に電磁波とされて いるものには周波数が与えられて区分されていることからもわかるように、「放射される」もので あり、それは具体的には波源の励振と密接に結びついているわけです。 そこでは、ベクトルポテンシャルAとスカラーポテンシャルΦを用いた波動方程式による説明がな されていました。これは、現在の「マックスウェルの方程式」にはなく、別の説明がなされている
動方程式となります。非常にややこしいのですが、これらの波動方程式の解は以下となります。
の項は急速に0に近づくので、遠くまで届くのは1/rの項だけとして上式が示されています。 現実世界では電磁波源は与えられ、私の教科書では線状アンテナやループアンテナの例が示 されていました。線状アンテナについては線素dsに対して考察がなされ、dE、dHが導出され、そ れからポインチングベクトル
現実には初期条件が入れられてある方向に偏向されているわけです。従って、電磁波というの は電磁波源から電磁的なエネルギーが径方向に球面状(範囲は初期条件で決まる)に伝わるも のと言えると思います。尚、教科書には物理的イメージとして図7が示されていました。
ここの説明から私は今、次のような解釈をしています。 電磁波源により、周囲空間が電磁ポテンシャル(A,Φ)を持つ特殊な状態になりその 状態の領域が時間と共に拡大していく。そして、時間tにおける点(x,y,z)の電磁ポテ ンシャル値は、(37),(38)式の値となる こうやって、私はある程度理解した気になっていたのですが、それでもまだ、私の中にもやもや が残っていました。それは、この説明は電波源と電波の説明であると言う事で、光源と光波、熱 源と熱流などへの応用展開が私の中でできなかったことと漠然と抱いていた座標系は何なのか という疑問が解けていなかったゆえでした。実はこの説明の時点では、単純にエネルギーだか ら真空中でも伝搬できるんだと現実的根拠もなく納得してしまっていてそれ以上のことは考えて もみませんでした。 それで、2013年頃、あてもなくマックスウェルの方程式についてネット検索をしていた時、そのも やもやを解決するものではありませんでしたが、偶然にも私にとっては大変衝撃的な記述を目に したのでした。な、なんと、 前述の(2)、(4)式はMaxwell自身が1865年に提示したオリジナル式ではない(※6) というものでした。それは、たまたま目にした日本語サイトの一つのウェブ論文に示されていて、 驚いて、国内サイトを当たったのですけど、その時は、それ以外には、その事実を暴露した上で 現在の方程式を改ざんされたものだと批判されていた1ブログと、少しだけ触れられていた1サイ ト記事くらいしかなく、やむ終えずその時初めて、英語サイトを当たったところ、英語サイトではそ の時、"Maxwell-Heaviside equations"という記事がいくつもヒットし、まず、(※6)は事実であ ること-すなわち、現在、「マックウェルの方程式」として教科書に載っていて教えられているもの は、電磁ポテンシャルを毛嫌いしたHeavisdeが書き換えたものであること-、そして関連する歴 史的なことを知って、いてもたってもおられず、最初は不十分な知識のまま速攻で記事を書いた のですが、更に色々と調べて得た知見を加えながら、内容は輻輳してはいましたけど、これまで、 Maxwellの方程式を考える①~Maxwellの方程式を考える⑤(以上'13/3記事)、Maxwellの方程 式(6)~訂正・新たな追記~('14)の合計6個のarticleをしたためてきています(2015年の1個は冒 頭で示したように抹消しました)。 それは、ただ単に(※6)の文面だけから見られるだけの話ではなかった重大な問題を含んでいる と考えたからです。 2013年頃、(※6)という事実を知った私は、James Clerk Maxwellの1865年のオリジナル論文を読 みたいという強い願望が湧き、その時、ダメもとで海外ネットを当たったところ、幸いにもそのオリ ジナル論文"A Dynamical Theory of the Electromagnetic Field"(電磁場の動的理論)が 転がっていました。やれうれしやてなもんでした。しかしながら、内容的には凡才の私にはわか りづらいところがあって色々とググっていたら、先に元になる論文をMaxwellが出していることを 知り、ケンブリッジ大学サイトにアクセスして、1855年のMaxwellの最初の論文集"On Faraday lines"も入手しました。ただ、ただでさえ英文読解力に劣る私の上に、彼の文章は(私にとっては) 非常にわかりにくいため(和訳をウェブ上に公開されている方もMaxwellの文章の難解さを指摘 されておられました)、膨大なこの論文、完全には読みこなせてはいません(^_^;)。 (尚、1855年の論文については最初にこのことを知ったウェブ論文の著者が無料で和訳をウェブ にアップされていました)。 尚、残念ながら、1873年に、更にクオータニアン(四元数)を用いて拡張されているという(難解さ のためか、論文の編者からも批判をされたらしい)"Treatise on Electricity and Magnetism" (電磁気学の教科書)は入手できていないので未読です。これについては批判を受けて、自ら切り つめ化を検討していたそうですが、それは、彼は1879年に胃がんで40代にして亡くなられた後の 1881年、1882年に改定版として出されたそうです。 以上と輻輳しますが、重要と考えているゆえに、前にも示しましたが、マッククウェルの方程式に 関する簡単な時系列的なものを再度以下にまとめておきます。 1820~1840年代:Faradayが数々の独創的実験により数々の画期的な電磁気現象を発見。 合わせて電磁気関連の独創的なidea(フィールド、近接作用等)を示した。 1850年代:それらFaradayの画期的発見が未だ理論化されていなかったため、数学の得意 な若きMaxwellはそれを自分が行おうと言う意欲に燃え、尊敬していたFaraday にそれを表明(そのときMaxwellが示した目的にFaradayは好意で応じている)す るとともに研究を開始した。 1855年前後:最初の論文集"On Faraday lines"を出版。理論の基になる概念・考え方に ついて示した。 1864~1865年:最初の研究が完成し、"A Dynamical Theory of the Electromagnetic Field"と題して、1864年にRoyal Societyの前で発表し、1865年に出版 (私がオリジナル論文と称している物はこれです)。 1873年:それを拡張したものをクオターニアン(quaternion/四元数)表記で書いた "Treatise on Electricity and Magnetism"を出版 1879年:40代の若さで胃がんで死亡 1881年:"Treatise on Electricity and Magnetism"改訂版第一版出版 1882年:"Treatise on Electricity and Magnetism"改訂版第二版出版 1880年代:アメリカのJosiah Willard Gibbsが、1840年代にHamiltonが二次元複素数を拡張し たものとして創設した難解なクオターニアンに代わるベクトル演算法を創設、 Oliver Heavisideがその確立に全面的協力して完成し、Heavisideはその適用第一 号として、Maxwellのオリジナル方程式の書き換えを行った(それが、現在「マック スウェルの方程式」と称せられて教科書に記載されているのである) 1887年:Heinrich Rudolf HertzがMaxwellが自らの方程式で予測していた電磁波の存在を 実証証明した(*) (*):海外サイトで目にしたのですが、Hertzは発見したことだけで満足してその応用にはまるきり関心を 持たなかったそうです。 尚、この発見に関してはNikola Teslaが絡んだ隠されて来た史実があります (⇒ニコラ・テスラ~なぜ不当な扱い?(4)参照) 実は、これを知った時、私自身恥ずかしながら「クオターニアン」については全く不案内でした。そ れで色々調べて、時系列的なものを知りました(→vectorとquaternionについて参照)。 その結果、当初疑問に抱いていた「なぜ、1865年の論文がx,y,z直交三軸座標系表記なっている のか?」「1873年になぜクォターニアンを用いたのか?」について氷解しました。Maxwellの生存 中には、未だ現在使われている「ベクトル演算法」というのは世に出ていなかったのでした。それ が世に出て来たのは彼の死後の1880年代(1881年に初めてGibsがたたき台になる物を提案した ようです)で、まだ1890年初頭には、クオターニアン派、ベクトル演算法派、クオターニアン派寄り の中間派で覇権争いをしていたそうです。前述のvectorとquaternionについてのarticleで参考引 用したPolar and axial vectors versus quaternionsというpdf論文に興味深い言及がなされていて、 「両派に前述のMaxwellの1873年発行の"Treatise on Electricity and Magnetism"が影響を与え た」と書かれていました。著者によれば、「Maxwellはこの論文で、『座標計算』と『クオターニアン 計算』を用いていた」そうです(前述のようにこの論文を入手できていないので未確認ですが)。 それはとにかくとして、上記の時系列的なものから明らかですが、歴史的事実として ・現在の前述の「マックウェルの方程式」と称せられている4つの式のうち、 (2)、(4)式はMaxwell自身は全くあずかり知らないものである(死後のこと ですから) ・Heavisideは毛嫌いして「電磁ポテンシャル」(ベクトルポテンシャル、スカ ラーポテンシャル)を消し去っているが、これは間違いなく、Maxwell自身 の示したMaxwell理論を完全に無視したものであった (なぜならば、Maxwellは「ベクトルポテンシャル」の物理的イメージまで 描いていて、そこからオリジナル式が出てきているのに対し、Heaviside は独自の物理理論から式を生み出したのではなく、Maxwellのオリジナ ル式から数学的に電磁ポテンシャルを消すように書き換えただけだか ら) であろうことは間違いないと思います。これも知られていませんが、この式が出て来た当時、この (1)~(4)の四つの方程式群は"Heaviside-Hertz equaitons"と称せられていたそうです。 "Hertz"の名前が出てくるのは、当時、Hertzも全く別に独自に切り詰めの検討をしていたようで、 そのためか、あるいは検閲等で関与したのかもしれません。 いつから現在のように(1)~(4)式がマックウェルの方程式と呼ばれるようになったかはよくわかり ませんでしたが、Einsteinはあの特殊相対性理論の論文"ON THE ELECTRODYNAMICS OF MOVING BODIES"の中で"Maxwell-Hertz equations"と書いており、また、ケンブリッ ジ大学を訪れた時、「Newtonより、よりMaxwellに影響を受けた」と述べていたそうですから、そん な所から、次第に「マックスウェルの方程式」と称せられるようになったのかもしれません。 しかしながら、私の推察ですが、EinsteinはMaxwellのオリジナル論文など読んではいなかった、 単に、彼も現在多くの人がそう思い込んでいるのと同じく、Heavisideが書き換えた現在「マックス ウェルの方程式」と称せられる(1)~(4)式だけで(それをMaxwellが作った式だと思い込んで)考 察したのだろうと強く確信しています。なぜなら、まるでMaxwellのオリジナル理論とは考え方が 異なるからです。ま、同僚の科学者が「歯がゆく」感じていたほど、Maxwellという方は英国科学 界の重鎮になってからも自分の功績を殊更吹聴したりせず、控え目すぎるくらいの方だったこと もあるのかもしれません(Maxwellは熱力学の分野でも功績を残しています)。そして、Einsteinは アカデミア科学コミュニティに属していないときにSRTを考えていたのですからそういう科学史に は疎かっただろうと思うのです。 いずれにしろ、上記歴史とMaxwellのオリジナル式及び彼の理論式を知った私としては、よく言 われている話とか教科書の記述を前述の歴史的経緯と兼ね合わせて考えるとき、これらには、 真実とは異なる虚構が入りこんでいると言わざるをえません。 恐らく、「工学者は計算の容易さからHeavisideが書き換えた現在『マックスウェルの方程式』と称 せられているものを好んだ」というのは事実だろうと思います。そして勿論、「1887年にHertzが電 磁波の存在を実証証明した」ことも事実です。しかしながら、Maxwellは決して彼のあずかり知ら ない今の「マックスウェルの方程式」と称せられているものから電磁波を予測したのではないこと は、前述のように、今のマックスウェルの方程式と称せられている物はMaxwellの死後にHeaviside が書き換えたものでありMaxwellのあずかり知らないもの、そして後述のようにMaxwellは自らの オリジナル式から求めていますので、そういう誤解を招く表現は欺瞞的だと思うのです。 言いたいことが一杯あるのですが、なぜ私が拘ってそういうことを言うかについてはおいおい説 明の中で明らかにしていきたいと思います。 何はともあれ、既に何度か示していますが、ご存知ない方も多いと存じますので、再度Maxwell が導出したオリジナル式を示します。尚、オリジナルのものは、成分表示であり、現在のSI単位 系と単位系が異なり、概念的にはまだ電磁気学が今のように固まっている時代のものではない のですが、それらも勘案して現在のベクトル演算法で示しますと以下の8個の式となります。 (オリジナル論文表記との相関はMaxwellの方程式(6)~訂正・新たな追記~参照)
従って、電磁気現象に絞って両者を比較しますと下記となります。 現在「マックスウェルの方程式」と称せられている物
Maxwellのオリジナル式
しました 誤りがありました。正確には、1865年のオリジナル式にはBという概念は出てこないのですが、 1873年の方には(50)式として出てきています 現在の電磁気学の教科書では、この(51)、(52)式はMaxwellとは無関係に提示されています。 (52)式は触れられていないものもあり、Eに関してよく出てくる式は、
「動電界」の場合のものです。この(54)式は前述で(33)式として使っています。 で、(52)式ですが、私の所有する教科書では、「電流が流れる回路があって、かつその回路が動 くとき」として導出されていました。したがって、(52)式は(54)式でv=0すなわち「回路が動かないと き」の式となります。 Maxwellは19世紀前半になされたFaradayが幾多の独創的実験で見出した幾多の電磁気現象の 画期的発見が1850年頃にはまだ完全に理論化されていなかったため、それまでの実験的知見 も合わせ、また尊敬していたFaradayが出していた独創的概念も合わせ、悉く一本の筋が通った 形で-そして研究開始時にFaradayに約束したように、自分の構築する理論が新たな実験のヒン トになることを目指して-の理論化を目指しそれが完成したとして1865年に発表したわけですけ ど、現在の電磁気学は、言うならば、Maxwellのそういう言説だけ採用し、確かに(1)(3)式はそう ですが、(2)(4)式はMaxwellが結果として出した真の「マックスウェルの方程式」ではなく、この Heavisideが書き換えたものをマックスウェルの所産だとし、元のものをばらばらに分解して、いか にもMaxwellとは無関係であるかを装って別の説明を与えて来たというのが実態だと思うのです。 前述で、この「いかにもMaxwellとは無関係であるかを装って別の説明を与えて来た」の典型的な 一例として、私の所有している教科書で(51)式がどのように記載されているかについて示してお きたいと思います。 ベクトル演算法をご存知なら下記のことはご存知だと思います。 Xをベクトル値とするとき、その回転
確かに、ベクトルポテンシャルAはベクトル値ですから、(51)(56)式から(4)が導出されます。 しかしながら、現在の電磁気学の教科書ではそういう説明はなされていません。私の所有する 教科書では次のような説明になっています。 磁界には真電荷に対応する「真磁荷」がないため、湧きだし口も吸い込み口もないので (4)式が成立するとあります。その上で、(56)式の公式から(51)式となるとされていました。 ここまで見てどう思われますか?要するに、この説明では、(51)式は物理理論的に求めたのでな く、(4)式から数学公式により「数学的に」導出しているということです。しかし、この時点ではベク トルAはベクトル値でさえあれば何でもいいわけです。 では、どのように「物理学的に」意味づけしているのでしょうか? (50)(51)式から
したがって、(57)式を(58)式に代入すると、
AもBと同様"solenoidal"なベクトル と考えると(証明がされていましたが省略します)
ということがわかりました。このように、Aは電流から直接求めることができるため、「電磁界解析」 というものは、「電流からまずAを求め、次に磁束密度Bを求める」という方法がとられています。 今、スカラーポテンシャルΦの式として
しています。ですから、私はここから、Aを「ベクトルポテンシャル」と呼称しているのではないかと 勝手に思っています(間違っていたらすいませんm(__)m)。しかしながら、この説明から、Aの「物 理的イメージ」をできるでしょうか? 私は、以前、「一体全体『ベクトルポテンシャル』って、物理的イメージはなんなんだろうか?」と 教科書には記載がなかったため、検索してみましたが見つかりませんでした。で、今は「なぜな いのか?」を知ったと言う事です。現在の電磁気学の説明が前述のように、「物理的」ではなく、 「数学的に」Aを出してきているからにほかなりません。ですから、長い間「計算の便宜のための 仮想的なもの」と思われて来たということも知りました。そんなものだったからこそ誰も物理的意 味づけをしなかったんだろうなと思いました。 しかしながら、そんな言い分は32年も前の1985年以前の話のはずです。私はネットサーフィンし ていて以下の事実を知りました。少なくとも物理学をやっている方達は学徒でもご存知のことの ようですが古い人間の私は知りませんでしたのでこれまた驚きました(ひょっとすると工学生は知 らないかもしれません)。 量子力学からの予測がなされ議論が百出したAB効果(アハラノフ=ボーム効果)が1985年に日 本の故・外村博士(日立研究所フェロー)により実証証明されたことにより、なんと、仮想的なもの と思われて来たこの「ベクトルポテンシャル」の物理的実在性が証明されたのです。 私はこの事実を非常に重く見ています。そしてそれが私をしてMaxwellのオリジナル方程式・理 論に殊更拘り、言及している理由の一つでもあります。なぜなら、Heavisideはベクトルポテンシャ ルを「直接測定できない(仮想的な)もの」として毛嫌いして、電磁ポテンシャル(ベクトルポテンシャ ルA、スカラーポテンシャルΦ)をオリジナル式から消去して、新たに(2)(4)式と書き換え、それが 現在では、「マックスウェルの方程式」と呼称されて教科書等に記載されていますけど、実在する ものとなるなら、俄然、元々のオリジナル式としての(43)(45)(または(51)(52))式の意味合いが増 してくるのは必定だと思うのです。例えば、前述のように、現在は、「湧きだしなし」として出てきて いる(4)式から「数学的に」(51)式を出していますが、そうではなくて、先に(51)(元は(43))式ありき ではないか、要するに(51)((元は(43))式の右辺の結果が左辺のBであるということです。 結果的ですけど、私は、現在「マックスェルの方程式」と称せられているHeavisideが数学的に書 き換えた英語サイトの用語を用いると"Maxwell-Heviside equations"というのは、電磁界の真相を ないがしろにしたいわば「改ざん」された式ということになると思うのです。私が目にした国内の1 ブログの「改ざんされた」という主張はその通りというのが今の私の思いです。 前述では、検索したがベクトルポテンシャルの「物理的(「物理学的」ではありません)イメージが 見つからなかったと書きましたけど、そのときはこれらの事実を知らなかったゆえでした。そう、 実は唯一、「オリジナル」理論・「オリジナル式」を出していたMaxwellだけは「物理イメージ」をな んと、 れは下図で、故・外村博士の前述の発見に関するウェブ上のscience essayの中にも引用されて いました(外村博士がこれを引用されたのは物理的イメージを示したものがこれしかなかったの だろうと思われます)。
「Maxwellは数学が得意であったが、物理的イメージを描くことにも優れていた」という説明を目 にしています。これもそういう彼の能力からのものだろうと思われます。彼は、「ヘルムホルツの 非圧縮性流体の完全渦流論」をアナロジーとしての理論構築のベースに置いているそうですか ら、こういう物理的イメージもそこからの所産だろうと思います。彼自身は、1865年の論文ではベ クトルポテンシャルに対して「電磁運動量(Electrromagnetic Momentum)」という名前を与 えていました。そして、彼は、Faradayが示した「電気緊張状態(Electrotonic-state)」に相当 するものと述べています(論文内で明記)。その上で、(51)(52)式からわかりますが、彼は、 B:「ベクトルポテンシャル」の「渦」から生ずる E:「ベクトルポテンシャル」の「時間的変化」から生ずる と考えたようです。Maxwellは自分が生み出した「電磁運動量」=「ベクトルポテンシャル」を実在 するものと考えていたという事です。彼が自らの方程式で推測した「電磁波」は1887年にHertzが 実証実験観測するまで当時の科学界からは信じられていませんでした。そして、この「ベクトルポ テンシャル」も同じで、長い間彼の物理的イメージは無視され「仮想的なもの」と科学界では信じ られてきたのです。ただ、こちらについては、発見から30年以上たつのに、電磁気の教科書では、 あってもコラム程度でしか触れられておらず、未だ「知る人ぞ知る」程度の状態です。私はここに 19世紀の物理学界と20世紀以降の物理学界の体制・考え方に大きな隔たりを感じました。 尚、誤解をされないように言っておきますが、私はMaxwellの物理的イメージが正しいとかそうい う断定をしているわけではありません。そうではなくて、彼は自分の出した理論を"reality"と結び つけて考えたことを高く評価しているだけです。そしてそれが本当の「自然科学」研究のスタンス ではないでしょうかと言いたいわけです。 ここで、Maxwellがこの研究に取り組むに当たったスタンスを示していると考えている1855年の 論文"On Faraday lines"の前書きから抜粋引用しておきます。 (...) the theory of the conduction of galvanism and that of the mutual attraction of conductors have been reduced to mathematical formula, but have not fallen into relation with the other parts of science. (...)The first process therefore in the effectual study of the science, must be one of simplification and reduction of the results of previous investigation to a form in which the mind can grasp them. The results of this simplification may take the form of a purely mathematical formula or fo a physical hypothesis. In the first case we entirely lose sight of the phenomena to be explained; and though we may trace out the consequences of given laws, we can never obtain more extended views of the connexions of the subject. If, on the other hand, we adopt a physical hypothesis, we see the phenomena only through a medium, and are liable to that blindness to facts and rashness in assumption which a partial explanation encourages. We must therefore discover some method of investigation which allows the mind at every step to lay hold of clear physical conception, without being committed to any theory founded on the physical science from which that conception is borrowed, so that it is beyond the truth by a favourite hypothesis. ((...)galvanism(流電気)の伝導理論と導体間の相互引力の理論は数学式に還元 されているが科学の他の箇所の関係には落し籠められていない。 (...)それゆえ、科学の効果的研究の最初のプロセスは、以前の研究の結果の、 心がそれらを掴む形への簡単化・還元化のものでなければならない。 この簡単化の結果は純粋な数学公式の形または物理的仮説の形をとるかもしれ ない。 第一のケースでは、我々は完全に説明すべき現象を見失う;そして、与えられ た法則の結果をトレースしても主題の関係のより発展的な観察を決して得るこ とはできない。 一方、もし、我々が物理的仮説を採用するなら、我々は現象を単に媒体を通し て見るだけであり、部分的説明が助長される仮定において事実に盲目的になっ たり軽率になりやすい。 それゆえ、我々は、その概念がそこからの借りものである物理科学で発見され ている任意の理論に任せてしまう-その結果、お気に入りの仮説によって真実 の外になる-ことをせずに、各ステップにおいて、心に明らかな物理概念を保 持することを許す、ある研究方法を発見しなければならない) 私でも読めるのですから、少なくとも電磁気学の市販教科書を書いているような科学者(特に物 理学者)はMaxwellのオリジナル論文を目にしていないはずはないと考えています。しかしながら、 オリジナル論文は無視されてしまったままになっています。未だ多くの人は、現在の教科書に掲 載されている「マックスウェルの方程式」はMaxwell作のものと思っており、Heavisideが書き換え たものであることを知らない方が多いようです。そして、驚きましたが、未だにウェブ上の解説で ベクトルポテンシャルを仮想的なものだと堂々と書いている方も見られます。 皆さまはこういう実態をどう思われますか? 外村博士の実験結果は昨日今日のものではなく、もう37年も前のものであり、よくあるような解 釈論ではなく、間違いなく電子線が波長/2だけずれた写真が提示されたものです。これでAB効 果にまつわるそれまでの大議論は終焉したと聞いています(ここまで実験証拠を見せつけられて もそれを認めない-認めたくない-昔のガリレイの望遠鏡にけちつけた天動説学者のような人 はいるそうですけど、私は自分の理論に合わないからと実験事実を否定するような人を「ほんも の」の物理学者とは認めません。しかし、そういう数学理論至上主義の物理学者は現にいて、そ れを堂々と主張しているのを見ると情けなくなります)。 しかしながら、どうしてそうなっているのでしょうか?私は完全にわかっています。 それは、1865年のMaxwellの論文"Dynamical Theory of Electromagnetic Field"の諸言を読めば すぐにわかります。 以下に抜粋引用しておきます。まず、冒頭で The most obvious mechanical phenomenon in electrical and magentical experiments is the mutual action by which bodies in certain states set each other in motion while still at a sensible distance from each other. The first step ,therefore, in reducing these phenomena into scientic form, is to acertain the magnitude and direction of the force acting between the bodies, and when it is found that this force depends in a certain way upon the relative position of the bodies and on their electric or magnetic condition, it seems at first sight natural to explain the facts by assuming the existence of something either at rest or in motion in each body, consisting its electric or magnetic state, and capable of acting at a distance according to mathematical laws. (電磁気実験におけるもっとも明らかな力学的現象は、それにより、ある状態にある 物体が、まだ互いに感知しうる距離にある間、互いに運動状態にある相互作用で ある。 それゆえ、これらの現象を科学的な形に還元する第一ステップは、物体間に働く力 の大きさと方向を確かめることであり、この力が物体間の相対的な位置と、それら の電気的・磁気的条件にある様式で依存することが見いだされるとき、ただちに、 その電気的または磁気的現象を含み、数学法則に応じて離れていて作用すること が可能である、互いの物体において静止または運動状態にある何かの存在を仮定 することによりその事実を説明することは自然に見える。) と述べ、これまで、そのようにして静電気、磁気、通電導体間の力学的作用、電流誘導の数学的 理論が作られて来たが、 In these theories the force acting between the two bodies is treated with reference only to the condition of bodies and their relative position, and without any express consideration of the surrounding medium. These theories assume, more or less explicitly, the exisitence of substances the particles of which have the property of acting on one another at a distance by attraction or repulsion. (二つの物体間に働く力は、ただ物体の条件とそれらの相対位置のみ参照し、 周囲媒体の何らかの明確な条件なしで取り扱われている。 これらの理論は、多かれ少なかれ、その粒子が離れた距離で互いに引力ま たは斥力が働く性質を持っている物質の存在を仮定している) (これは所謂「遠隔作用説」ですね) とし、「その理論の完全な発展形は、二つの荷電粒子間の間の力が、それらの距離と同様それ らの相対速度に依存すると仮定することが必要であることを発見したMM.W.Ewverらによりなさ れたが、速度に依存する力を持って離れた距離で働く粒子を仮定することの力学的困難性から、 その理論を基本的なものと考えることに抵抗があった」と述べ、 I have therefore preferred to seek an explanation of the fact in another direction ,by supposing them to be produced by actions which go on in the surrounding medium as well as on the excited bodies , and by endeavouring to explain the action between distant bodies without assuming the existence of forces capable of acting directly at sensible distances. (それゆえ、私は、他の方向での事実の説明を、それらが励起された物体に 対するのと同様、周囲媒体の中で継続される作用により生じていると仮定し、 感知できる距離で直接作用できる力の存在を仮定せずに離れた物体間の 作用の説明に努めることによる説明を探索するほうを選んだ。) と書いています。 要するに、Maxwellは「近接作用説」すなわちFradayが考えたと言われている"field(場)"で考える ことを宣言しているわけです。彼は、続いてまず、ずばり、 The theory I proposed may therefore be called a theory of Electromagnetic Field, because it has to do with the space in the neighborhood of the electric or magnetic bodies (私の提案する理論は、それゆえ、電磁場理論と呼ばれるかもしれな い、なぜならば、それは電気的又は磁気的物体の近傍の空間を扱っ ているから) と述べ、更に it may be called a Dynamical Theory, because it assumes that in the space there is matter in motion, by which the observed electromagnetic phenomena are produced. (それは、動力学的理論と呼ばれるかもしれない、なぜならば、その 空間にそれによって観測される電磁現象が生ずる運動状態の物質 があるから) と書いています。タイトルの"Dynamical Theory of Electromagnetic Field"はこんなところからのも ののようですね。そして、だんだんわかって来たと思いますが、決定的なのは次の文章です。 The electromagnetic field is that part of space which contains and surrounds bodies in electric or magnetic conditions. It may be filled with any kind of matter, or we may endeavor to render it empty of all gross matter, as in the case of Geissler's tubes and other so-called vavua. There is always, however, enough of matter left to receive and transmit the undulations of light and heat, and it is because the transmission of these radiation is not greatly altered when we are obliged to admit that the undulations are those of an æthereal substance, and not of the gross matter, the presence of which merely modifies in some way the motion of the æther. We have therefore some reason to believe, from the phenomena of light and heat, that there is an æthereal medium filling space and permeating bodies, capable of being set in motion and of transmitting that motion from one part to another, and of communicating that motion to gross matter so as to heat it and affect it in various ways. (電磁場は電気的または磁気的条件下にある物体を含み取り囲んでいる。 それはある種の物質で充満されているかもしれないし、または、我々は、 それをガイスラー管やその他の所謂真空の場合のように、それを総体が 空であると表そうと努めるかもしれない。 しかしながら、光や熱の波動を受け伝えるのを担う十分な物質が存在し、 それは、これらの放射の伝搬が、我々がその波動はエーテル状物質のも のであり、その存在は、ただ、なんらかの様式でエーテルの運動を修正 する総体のものではないことを認める必要があるときに、大きく変わらな いためである。 我々は、それゆえ、光と熱の現象から、運動状態におかれ、その運動を 一つの部分から他の部分に伝え、その運動が、種々の方法でそれを加 熱し影響するように総体に伝わることが可能な空間を満たし物体に浸透 しているエーテル状媒体があることを信じるいくつかの理由がある。) そう、Maxwellは理論構築に置いて、周囲媒体を考え、直接「エーテル(æther)の運動」として 「エーテル」に言及しています。私は最初、当時はまだ「エーテル(æther)」が一般的知識だったか らかと思っていたのですが、そうではなくて、「近接作用」のスタンスからの彼の必然的論理的結 果だったのでした。 「エーテル」はギリシャ時代から考えられてきていたものですが、直接検出できていたわけでもな く、「あるとするとうまく説明できる」とされてきたもので、その性状などはわかってはいません でした。あのNewtonもわからないと言っていたようです。で、19世紀になって、光が波動であるこ とが科学界で主流派として確定したとき、それを伝達するものとして「光学エーテル(Luminor æther)」 という発想が生まれました。 しかるに、MM実験の結果が「Lorentzが作った実験理論」と合わない小さな値であった(相対性 理論学者を始めとするEinsteiniansや物理学者らの説明とは真相は異なることについて私は既 に直近では続・相対性理論への疑念(26)~マイケルソン=モーリー実験 & Dayton Miller再び~ で示しましたが)ことがあり、FitzGeraldが1887年に実証根拠のないad-hocなことを言い出し、それ にLorentzらが乗かって、1904年に"Lorentz Ether Theory"(1904年が最終版)を提示したのですが、 未だその性質もわかっていなかったエーテルにあまりにもad-hocな性質を与えるものであり、一 方で、1905年にEinsteinがSRTを発表し、その際、彼はエーテル否定(否定したのではなく「不要」 と云っただけという説もあります)をし、理論は見かけ上、それが不要となっていたため、エーテル 研究が次第に影を薄め、そして、1919年のエディントンの日食観測結果報告(既に散々書いてき ましたが、いわば「捏造論文」です)が1915年発表のGRT(General Relativity Theory)の証拠だと エディントンら、当時のEinsteiniansらは強弁し、更に、そこから、いわば、「イケイケどんどん」で それまで続いて来たLorentz-Poincaré派との覇権争い勝ったとばかりに、SRTとGRTを一貫した ものだとこれまた強弁して(Lorentz-Poincaré派にはGRTに対抗するものがありませんでしたから)、 これも正しいのだという風になってしまい、1922年頃からSRTは完全にmain streamになったよう で(年代・事情については続・相対性理論への疑念(31)~G.O.Mueller調査報告紹介再び~ ③参照。尚、どうやらGRTの方は、理解してもないメディアが英雄願望の一般大衆を煽り、一般 大衆は勿論のこと、当時の物理学コミュニティでも理解していない物理学者が多かったけれども、 よくある「風」みたいな形で一般大衆はEinstein="Genius & Hero of science"と思い込み、中身を 知らないまま「すごい理論だ」として、上っ面の評判ばかりが広がっていたというのが真相らしく、 戦前は物理学界ではGRTはまだmain streamにまではなっていなかったようです)多分にそれが 決定的になって、エーテルというのがタブー扱いになり、何か昔の誤った概念みたいにされ、死 語扱いされているのだろうと思います。 しかしながら、隠され無視されていますけど、既に本コーナで示してきたように、当のEinstein自 身は1920年のLeiden大学における物理コンフェランスではっきりと「電磁波が伝わるためには エーテルが必要である。このことをLorentzにも伝える」と明言(すなわち"change in mind")した歴 史的記録が暴露されています。Einsteinは直接言及せずその名も使っていませんけど、1915年 発表のGRTは間違いなくエーテルというか周囲媒体の存在に基づいているという主張も目にし ています(彼の重力場理論がそうだと)。確かにGRTは1915年に発表、上記のLeiden大学での 主張はわずか5年後の1920年ですから、この主張は十分説得力があると思います。それに物 理学界はご都合主義的と言うか、「真空はempty」として「Æther」の存在を否定してタブー視して きたのに、「ビッグバン宇宙論」が観測結果をうまく説明できないとなったら平気でダークマター なる仮説を作って理論の支柱にして探すと言うことをやってますけど、「そんなもんエーテルそ のものじゃないか」とそういうご都合主義を揶揄している方々もおられます。 確かに私も長い間、「エーテル(æther;近年は混同を避けるためか"ether"と言わずAetherと書か れることが多いようですが、Maxwellはこのような表記をしています)」など死語になっている昔の 概念だと思っていました。多分にそう誰かから聞いていたからだと思います。しかしながら、調べ てみると、なぜそうなったのか-例えば実験的に否定されたのか-というのがきちんと示されて いない気がしました。ですから、どうもそういうことになったのは、Einsteinが発端だとしか思えな くなりました。なぜなら、当時SRT反対科学者だった方達(特に実験を重んじる科学者、実験物 理学者、MM実験のMichelson(アメリカのノーベル物理学賞受賞第一号者)、Dayton Miller、サ ニャック効果実験のSagnacなど)は、エーテル派でSRT反対派でありMichelsonがその後行った MM実験を宇宙規模で行ったMichelson-Gale実験やサニャック実験はエーテルドリフトを見出す ためになされた実験(1890年代にケルビン卿が呼びかけた)でした。Einsteiniansは勝手に相対性 理論証拠だとしていますけど、実験をやった本人たちはエーテルドリフト実証試験だとしています ので、これらの実験を相対性理論の証拠扱いするのは厚かましく独善的ではないでしょうか? 結局のところ、強引な形でSRTが物理学のmain streamにされ(→続・相対性理論への疑念(31) ~G.O.Mueller調査報告紹介再び~③参照)、「エーテル(æther)」はそれとは矛盾するためとい う意味だけで嫌われ否定されタブー視されたものだと思うのです。完全に実験検証的に否定さ れたのではないということです。そして、このMaxwellのオリジナル理論などもあり、漠然として いたその性状に関する研究が進みだした矢先の1905年、SRTの発表とEinsteinのその時なし た言動が、それまでの「エーテル(æther)」研究を捨てさせてしまって何かわからないままタブー 視されてしまったというのが実態ではないでしょうか?そういう指摘は海外サイトにもありました ので、私一人の思いではありません。 それゆえ、Maxwellのオリジナル理論に誰も言及せず(「できず」というのが事実でしょう)、私が指 摘したように、現在の電磁気学はおかしな説明でごまかしをしてきたでしょう。 一度調べてみてください。「なぜ真空中でも電場、磁場更には重力場などという状態があるのか?」 「なぜ真空中でも電磁波が伝搬するのか?」について統一した明確な説明をしているテキストを 目にしたことがありません(個別の見解をされている方はおられるようですけどね。ま、同じ指摘 をされていたサイトを目にしていますので、私一人だけ知らないわけではないと思います)。 結局、説明なしでそうなるのだと言っているだけなのです。前にも指摘しましたが、「マックスウェ ルの応力」というのがあります。真空中でも成立するものですが、電磁気学の教科書はしら~と そのまま式を出していますけど、どうして真空がemptyなら「応力」などというものがあるのかに ついては全く説明されていません。おかしいと思いませんか? 実際、それまで皆「遠隔作用説」だったのに対して、「場(filed)」という概念的なものを示したFaraday、 それに賛同したケルビン卿及びMaxwellらは、上記のMaxwellの諸言から伺えますが、それを 「周囲媒体(medium)」の働きと考えての「近接作用説」だったわけです。ですから、彼らはちゃん と場の物理的要因を描いていたのです。ところが、20世紀物理学は、「エーテル(æther)」をタブー 視してしまい、「真空=empty」などと言っているために、前述の「なぜ場と言うのができるの?場 の物理的(物理学的ではありません、real worldでのrealityの世界の話です)意味は何?」「なぜ 真空中でも電磁場は伝搬できるの?」「真空中のマックスウェルの応力ってどういうことなの?」 などということを説明できず、逃げてしまっているわけです。 「自然がそうなっているから仕方がない。考える必要はない」などというなら、少なくとも電場、磁 場、電磁波については卑怯な逃げでしかありません。なぜなら、ちゃんと1865年Maxwellは自分 の論文の中で説明しているのですから。そして、Maxwellが示した式が全く使われていない、一 部しか使われていないというのならまだ話はわかりますが、中にはMaxwellが最初に示したこと などほうかむりしてあたかも無関係であるかのようにして、全て使われているのです。ということ は、現在、学徒が大学で習っている電磁気学に基本的な誤りがないのなら、1865年にMaxwell が示したオリジナル理論には間違いがないということにほかなりません。 ですから、明らかに「タブー視されている『エーテル』がその理論の基礎にある」がためだけで、触 れることができないと言うだけにほかならないと思うのです。 穿った見方かもしれませんが、前述の故・外村博士の実証実験結果というのは物理学者にとっ て諸刃の刀になっているのではないかと思うのです。故・外村博士はMaxwellの論文から図8を 引用されていますが、過去誰も引用してこなかったタブー扱いのものではなかったかと思うので す。今までは「計算のための仮想的なもの」とされてきたゆえに前述のような説明で済んだわけ ですけど、「実在のもの」となるとそういう今までの説明でお茶を濁し続けるわけにはいかないは ずです。物理的意義を説明する必要性が出てくるからです。 しかしながら、そのタブー視され20世紀物理学界において研究が捨てられてしまったゆえか、 「エーテル」が真に存在しないという実証的証拠など目にしたことありません。MM実験は実証証 拠では決してありませんので持ち出さないように。そして、もしSRTなどを証拠だと言うなら、前述 の1920年のEinsteinの言説を合理的・論理的に説明してください。曖昧な物言いが多いEinstein ですがそんな理論の元祖の彼が「はっきり『エーテル』を認めたのです!」。ですからどんな詭弁・ 屁理屈を持ち出そうとこればっかりはダメです。不都合故に隠されて来た事実です。 もし、私の認識に誤りがあると言うのなら、是非理由を教えていただきたいものです。 こうやって、こんなところにまで、1905年に発したEinsteinの言動と彼のSRTが影響しているすな わち現在の物理学を歪ませてしまっているということに心ある方は是非気が付いていただきたい ものです。 そういう背景を考え、今時タブー視されている「エーテル(æther)」を持ち出すだけで「とんでも扱い」 されてしまうことはわかっていますけど、そういうことを言ったり考えたりされている方に是非教え ていただきたいことは、その存在を完全否定している確証バイアスのかかっていない(要するにS RTの影響が入っていない)「実証観測結果」があるか否か、あるならそれはどういうものかという ことです。 どちらが論理的・合理的か考えて、私は"medium"はあるのではないかという思いに達しました。 私には他に、これも不当に「とんでも扱いされてしまっているNikola Teslaの研究内容も考え合わ せてのことです。 そういう思いもあって、殊更Maxwellのオリジナル理論に興味が湧き、本コーナーでオリジナル方 程式に言及するようになったわけです。 勿論、Faradayの実験が全てだったかどうかは不明ですし、Maxwellの理論が絶対かと言うと、そ れも不明です。私は単純に"believer"にはなりません。ですが、あるものに対してより論理的・合 理的かどうかで判断しています。で、前述のように、今の電磁気学ではごまかしていますけど、 Maxwellの1865年のオリジナル方程式は全て現在の電磁気学の中に出てきているという事実か ら間違いなく、彼が自負していたように、Maxwellの1865年のオリジナル理論はFaradayのなした 画期的電磁気実験を全てうまく説明していることになります。それに留意する必要があります。 ただ、もし電磁気に関する実験がまだ不十分だったらどうかということもありうると思うのです。 確かにMaxwellが自ら検討して結論付けたように、「電磁波」はMaxwellの方程式からは「横波」 のみが出てきます。一方、とんでも扱いされていますけど、Nikola Teslaが見出した「テスラ波」 は彼によれば「縦波(longitudinal wave)」です。このギャップですが、Teslaは"longitudinal Electric Wave"と称していました。「電磁波」ではなく「電気波」と言っているわけです。 正統派は従来知見だけで全否定しますけど、人間の知恵などしれたものです。やりもせずに頭 から全否定するなどというのは愚の骨頂です。Faradayは彼の一連の電磁誘導の実験に対し当 時の「数学理論至上主義」連中から「ペテン師」と中傷された事実、電気の本格的な研究の元に なった「カエルの解剖実験」から生体電気を発見したLuigi Galvaniが当時受けた数々の中傷の 事実を是非知っておくべきです。その当時だからではありません。今も何も変わらないのです! 尚、この諸言ではそれまでなされた実験結果やそれに基づく権威(ケルビン卿=W.Thomoson)ら の考察など理論化にあたって考慮したことの概要も示されています。そして、オリジナル方程式 (彼は「電磁場の一般的方程式(the general Equaitons of the Electromagnetic Field)」 と称しています)が何を表すかを以下として示されています。 (A)The relation between electric displacement, true conduction, and the total current, compound of both. (電気変位、真電導、両方の複合の全電流) (B)The relation between the lines of magnetic force and inductive coefficient of a circuit, as already deduced from the laws of induction. (既に誘導法則から引き出された磁力線と回路の誘導係数間の関係) (C)The relation between the strength of a current and its magnetic effects, according to the electromagnetic system of measurement. (電磁測定系による電流の強さとその磁気的効果の間の関係) (D)The value of electromotive force in a body, as arising from the motion of the body in the field, the alteration of the field itself, and the variation of electric potential from one part of the field to another. (場における物体の運動、場自身の交番、場の一部から他の部分への電気ポ テンシャルの変化から生ずるような、物体内の起電力の値) (E) The relation between electric displacement, and the electromotive force which produces it. (電気変位とそれを生ずる起電力の間の関係) (F) The relation between an electric current, and the electromotive force which produces it. (電流と、それを生ずる起電力との間の関係) (G) The relation between the amount of free electricity at any point, and electric displacements in the neighborhood. (任意の点の自由電子量とその付近の電気変位の間の関係) (H) The relation between the increase or diminish of free electricity and the electric currents in the neighborhood. (自由電子の増減とその付近の電流との間の関係) これら(A)~(H)はそれぞれ前述の(40)~(47)式に対応しています。 上記で、"electric displacement(電気変位)"はDのことです(一般には「電束密度」と称されていま すが、日本語でもこのような呼称もあり、私の教科書には先にこの名称が使われていました)。 また、"electromotive force"はそのまま「起電力」と和訳しましたが、電界(電場)の強さに相当する ものとしての意義です(現在の「起電力」は定義は単位系の差だけです。したがって、(45)式は オームの法則の一般形-私の所有する教科書でそう書かれていました-になります)。 さて、あれこれ書いて来たくせに実は、1865年論文、どうやら以前はきちんと読んでいなかったよ うで、今回改めて特にその中の電磁波関連についてしっかりと読み直しました。以下に引用紹介 しておきたいと思います。 諸言のところで驚くべきことが書かれていました。後述の、私が冒頭で後述すると書いた最近英 語サイトで目にした記事と完全にリンクしているものです。 それは書かれいた次の言葉です。 The conception of the propagation of transverse magnetic disturbances to the exclusion of normal ones is distinctly set forth by Professor Faraday in his “Thoughts on Ray Vibrations.” The electromagnetic theory of light, as proposed by him, is the same in substance as that which I have begun to develop in this paper, except that in 1846 there were no data to calculate the velocity of propagation. (法線方向のそれ[擾乱]に対する横波磁気擾乱の伝搬の概念はFaraday教授 により彼の「光波動についての考察」によりはっきりと発表されている。光の電 磁気学理論は、彼によって提案されたように、1846年には伝搬速度を計算する データがなかったことを除き、私がこの論文で発展させ始めたように実質上同じ である。) Maxwellはこの論文では『電磁波(Electromagnetic wave)』という用語は使っていません。草創期 ゆえだと思いますが上記のように"transverse(横波の)"magnetic disturbunce(磁気擾乱)"としてい ます("electromagnetic disturbance"というのも出てきますけど)。 で、驚いたのは、「電磁波」とか「光は電磁波である」という思考は、Maxwellのオリジナルではな く、先にかのFaradayが既に19世紀前半に論文で示していたということです。Faradayという方の凄 さがここにも現れています。Faradayを尊敬していた若き頃のMaxwellは、約10年かけて完成した 自らの理論で、先にFaradayが深い思考から提起していた「光は電磁波である」ということを理論 的に証明したということでした。 実は、冒頭で後述するとしていた話ですが、英語サイトに、Faraday’s Secret 1832 Letter Reveals Electromagnetic Waves Prediction という記事がありました。その記事に、 One hundred eighty years ago today, on March 12, 1832, Faraday wrote a secret letter predicting the existence of electromagnetic waves. (180年前の今日、1832年3月12日、ファラデーは 電磁波の存在を予測する 秘密の手紙を書いた。) と書かれていました。 その手紙は、ロンドンのRoyal Society議長宛のもので、一世紀以上金庫に眠っていて、その後、 一度だけ、1937年にSir William Braggによって開かれたそうで、この記事の著者によれば、この 手紙の唯一のオンライン発行は、Garratの"The Early History of Radio"くらいだそうです。 で、手紙の前文が引用されていましたので、全文孫引用しておきます。 Certain of the results of the investigations which are embodied in the two papers entitled ‘Experimental Researches in Electricity' lately read to the Royal Society, and the views arising therefrom, in connexion with other views and experiments lead me to believe that magnetic action is progressive, and requires time, i.e. that when a magnet acts upon a distant magnet or piece of iron, the influencing cause (which I may for the moment call magnetism) proceeds gradually from the magnetic bodies, and requires time for its transmission, which will probably be found to be very sensible. I think also, that I see reason for supposing that electric induction (of tension) is also performed in a similar progressive way. I am inclined to compare the diffusion of magnetic forces from a magnetic pole to the vibrations upon the surface of disturbed water, or those of air in the phenomenon of sound; i.e. I am inclined to think the vibratory theory will apply to these phenomena as it does to sound, and most probably to light. By analogy, I think it may possibly apply to the phenomenon of induction of electricity of tension also. These views I wish to work out experimentally; but as much of my time is engaged in the duties of my office, and as the experiments will therefore be prolonged, and may in their course be subject to the observation of others, I wish, by depositing this paper in the care of the Royal Society, to take possession as it were of a certain date; and so have right, if they are confirmed by experiment, to claim credit for the views at that date; at which time as far as I know, no one is conscious of or can claim them but myself. (『電気における実験研究』と題した二つの論文にもりこまれた発見の結果の 確信は、のちにRoyal Societyに対して読まれ、そこから出て来た見地は、他 の見地や実験と結びついて、私をして、磁気作用が進行的で時間を必要と する、すなわち、磁石が離れた磁石や鉄片に作用するとき、影響を及ぼす 原因[となるもの](私は今のところ磁性と称しているが)は、磁性体から次 第に成長し、その伝搬に時間を必要とする、それは恐らく大きく感知され ることが発見されるであろう。 私はまた、電気誘導(緊張の)がまた、同様な進行形でなされると仮定する 理由を見ていると考えている。私は磁極からの磁力の拡散を、乱れた水の 表面または音の現象におけるそれ上の振動と比較する気になっている; すなわち、私は振動理論が音に対してなされるそして最も恐らくでは光に 対してなされるようなこれらの現象に適用する気になっている。 アナロジーにより、私はまた、恐らく電気緊張の誘導現象に適用してよい と考えている。 私はこれらの見解を実験的に見出すことを望んでいる;しかし、私の時間 の多くは私のオフィスの義務に取られていて、それゆえ、その実験は長期 に渡り、それらの進路に置いて他の観測の対象になるかもしれないので、 私は、この論文をRoyal Societyの注意の元での保証により、あるときま で占有することを望んでいる;もし、それらが実験で確定するなら、その 日付での見解に対する優先権を主張する権利を持っている;私が知る限り その時には誰もそれらを意識していないか私以外は、主張できない。) そう、彼は既にそのideaをなんと1832年にもう抱いていたということです。そして、上の手紙の文 面から「秘密の手紙」とした理由がわかりました。Maxwellが1865年の論文で言及していますが、 Faradayは論文を公式に出したということは、その後、自分のideaを確信できるようなことを実験 の中でつかんだということでしょうね。 Maxwellの論文からの引用を続けます。 The general equations are next applied to the case of a magnetic disturbance propagated through a non-conducting field, and it is shown that the only disturbances which can be so propagated are those which are transverse to the direction of propagation, and that the velocity of propagation is the velocity v, found from experiment such as those of Weber, which expresses the number of electrostatic units of electricity which are contained in one electromagnetic unit. This velocity is so nearly that of light, that it seems we have strong reason to conclude that light itself(including radiant heat, and other radiations if any) is an electromagnetic disturbance in the form of waves propagated through the electromagnetic field according to electromagnetic laws. (一般方程式が次に非導体場を通して伝搬する磁気擾乱の場合に適用され、 そのように伝搬できる唯一の擾乱は伝達方向に横向きのものであり、伝搬 速度は、電磁単位に含まれる電気の静電単位の数で表示するWeberのもの のような実験からわかった速度vである。 この速度は光速に大変近いので、我々は、光自身(放射熱ととにかくその他 の放射を含む)が、電磁法則によって電磁場を伝搬する電磁擾乱であるとい う強い理由を持っている。) ここでは、"electromagnetic disturbance(電磁擾乱)"と書いていますね。 「一般方程式(general equations)」というのは、私がオリジナル式と称している前述の(40)~(47)式 のことです。 その理論展開がされていますが、論文は成分表示です。論文そのままの記号ではわかりにくい こともあり、また、オリジナル式で一部4πの扱いが現在のSI単位系でのものと異なるところがあ りますので、以下ではできるだけベクトル演算法表示に従い、結論に近い方の部分で記号表記 を下記にしたがって変えた上で(x,y,z)成分表示を使って読み替えをしておりますが、基本的には 彼の論法に従っています(但し、説明順序を一部変え、また、書かれていない途中経過も補足し ています)。 [本稿記号と論文記載記号の比較]
------------------------------------------- (43)式より
ここから先は、Maxwellがなした成分表示で進めます。(71)式を成分表示で書くと
------------------------------------------- このようにして、Maxwellは、言わば 磁化の方向が平面内にある平面がその法線ベクトル方向に(103)式の速度Vで 動いていく平面波が生成される(※7) ことを ・場の中の媒質が完全な誘電体(dielectric)であるなら、真電導(すなわち導体電流J) はない ・回路は静止している を条件にして、自らの方程式のうち(42)~(46)式より見出したわけです。 ここに至ってやっと電磁気学のテキストの電磁波が「平面波」で説明されて来た理由が理解でき ました。ただ、Maxwellもなぜ平面波として解析を進めたかまでは書かれていませんでした。 以上より、Maxwellは This wave consists entirely of magnetic disturbances, the direction of magnetization being in the plane of the wave. No magnetic disturbance whose direction of magnetization is not in the plane of the wave can be propagated as a plane wave at all. (この波は完全に、磁化の方向が波の面内にある磁気擾乱からなる。磁化の 方向が波面内にない磁気擾乱は全く平面波として伝達できない。) と述べ、 Hence magnetic disturbances propagated through the electromagnetic field agree with light in this, that the disturbance at any point is transverse to the direction of propagation and such wave may have all the properties of polarized light. (それゆえに、電磁場を通って伝搬する磁気擾乱は、これにおいて、任意の点 の擾乱が伝搬方向に対して横向きである光と一致し、このような波は偏光の 全ての性質を持つかもしれない) とまず結論付けています。 「magnetic disturbance(磁気擾乱)」と書いていますが、前述の式の展開で最後は磁気の式になっ ていますから、そういうこともあったのかもしれません。 その後で、当時測定されていた空気に対する諸元(彼の式での単位系でμ=1としています)を用い ての速度Vの計算値と当時、光行差と認められている地球の軌道から求めた光速とを比較して います。彼の示しているものは下記。 ・光速=308,000,000 m/s ・算定した速度V MM. WeberとKohlauschの電磁気実験を用いると:314,858,000 m/s M.Foucaultの厳密値を用いると:298,000,000 m/s これより、Maxwellは、 Hence the velocity of light deduced from experiment agrees sufficiently well with the value of v deduced from the only set of experiments we as yet possess. (これより、実験から推定された光速は我々が未だ有している唯一の実験から推 定した速度vと十分よく一致している。) と述べています(「実験から推定された光速」とは「光行差と認められている地球の軌道から求め たもの」という意味だと思います)。 Maxwellがこのように考察を進めたのは、前述のように先にFaradayの卓見があったためと思わ れます。「平面波」というのはその中での試行錯誤から見出したのかもしれません。 長くなり過ぎました。私の中にあるもやもやはまだ解消されていませんし、今回もMaxwellの理 論の中身までは言及しませんでしたが、今回はここまでとします。 -------------------------------------------------------------- (お詫び) 私は(45)式を式だけ見て思い込みで前に記事を書きましたが、改めてMaxwellの論文を見て自 分の思い込みに気が付き、そのarticleを削除しましたm(__)m 今回、Maxwellが考えていたのも、(45)式にμ(v×H)が入っているのは前述の私の教科書の説 明と同じく「回路が動くとき」のものであることがわかりました。 尚言い訳がましいですが、これまで(52)式を見た時、式にv×Bが入っているため電荷が電磁界 内で動く時の「ローレンツ力」として出てくるものだと早とちりしていました。 磁束密度B、電界Eのあるところで電荷qが速度vで動くと、
(本お詫び追記)('17/8) "AN OVERVIEW OF MAXWELL’S TREATISEON ELECTRICITY AND MAGNETISM"(pdf論文 のためリンク省略、ググると出てきます)という海外サイトpdf記事の中で、私が当初考えてい たこの「ローレンツ力」に関して、(105)式相当のものを示し、実はMaxwellが先に既に見出して いたのだと書かれていました。どうやら、エレクトロンというのは1891年にケルビン卿が最初に 提示したものであり、Maxwellが論文を提示したころはまだそういう概念がなかっただけで、導 体内の電子を考えればまさにこのMaxwellの式はローレンツ力に相当すると書かれていました。 私の考えたのは私一人の早とちりではなかったということです。 勿論、物理的な意味では限定的であり、物理的な意味での導出法も異なりますけど、全く入っ ていないというのはやはり、現在の「マックスウェルの方程式」と称せられている物をMaxwell の所産だと誤解されての主張だという私の当初の思いは誤ってはいなかったと改めて思って いるところです。 ('17/7) 目次に戻る |