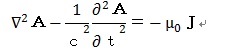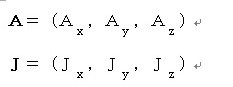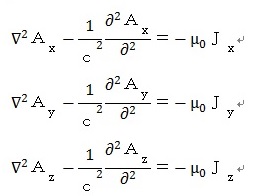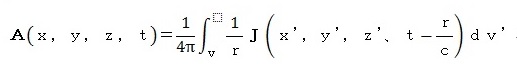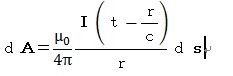Maxwellの方程式を考える（5）電磁波（続き）

（4）項でMaxwellの方程式からのベクトルポテンシャルＡに関する波動方程
式

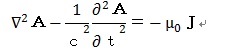
を示しました。直角座標系で表すと、

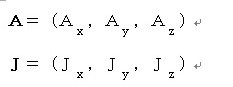
で、

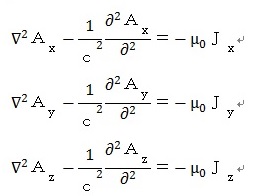
となります。これは非同次波動方程式で簡単には解けませんが、この形の
波動方程式に対してはグリーン関数（ポアソン方程式の一般解を求めるの
にも用いられるガウスの発散定理から導出されるベクトル公式）というもの
を用いて巧妙なやりかたでキルヒホッフが解を求めていて、そこに更に、電
磁波は有限の速度で伝搬されるため、全ての波源が原点から有限な距離
以内にのみ分布し、有限時間以前に発生したとすると境界面を無限遠に
遠ざけることができるので、そのときは境界面条件（Ｖの外表面における面
積分で表される項）を0とおくことができることから、このとき解は

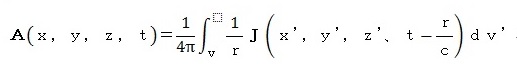
となるとありました（昭和42年発行、電子通信学会編「電磁気学」コロナ社）。
（ｘ、ｙ、ｚ）点も（ｘ’，ｙ’，ｚ’）点もＶ内の点です。右辺はＶ内にある電磁波源
を示しています。この式は
　時間ｔにおける（ｘ、ｙ、ｚ）点のベクトルポテンシャルは時間（ｔ－ｒ/ｃ）
　におけるＶ内の全ての点の電流密度Ｊの寄与の合計となる
ことを示しています（と、私は理解しました）。

・・・といかにも理解できたかのようにえらそうに書いてしまいましたが、浅学
非才の私はグリーンの定理とかそれを用いてのポアソン方程式の解は理解
できたのですが、情けないことにこのキルヒホッフの巧妙な解法はよく理解
できていません(^_^;)。ブラックボックスが大嫌いな私としてはですからここで
妥協してしまってはいけないのですが、とりあえずはしょって上の解だけ見て
考えているわけです。

ただ、それでもイメージしにくいので、電流素辺という仮想的なものを考えれ
ば、右辺の積分内に1/ｒの項があり、ｒは（ｘ、ｙ、ｚ）点の（ｘ’，ｙ’，ｚ’）点から
の距離ですから、電流素辺からの電磁波は基本的には球面波となります。
上記の教科書には

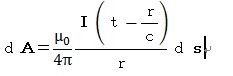
という式（ここでｄｓ：電流素辺の線素ベクトル、Ｉ：その上の電流の強さ）が記
載されています。

これで少しはわかった気が進みましたけど、前述の教科書はここから一般的
なＥ，Ｈに還元して説明を進めていますのですごくもどかしい気がしており、完
全には理解できておらずいくつかの疑問がまだ私には残っています。

いずれにしろ、今や、ベクトルポテンシャルは計算上の仮想的なものではなく
実在するものであると実証証明されていることを考慮すると、これまでのよう
にＥ，ＨでMaxwellの方程式や電磁波を考えるのではなくあくまでベクトルポテ
ンシャル（拡張すると静電ポテンシャルを含めた電磁ポテンシャル）で全てを
考え直すべきではないかと思うのですが・・・
・・・と言いながら、情けないことに私自身、ポテンシャル特にベクトルポテ
ンシャルという存在を十分理解できていませんが(^_^;)。

目次に戻る
次へ