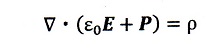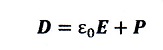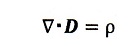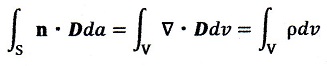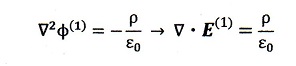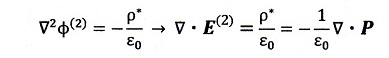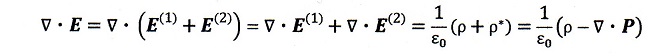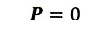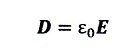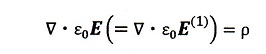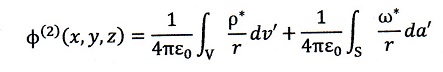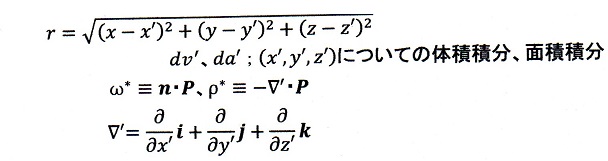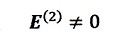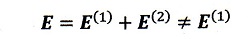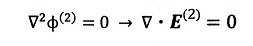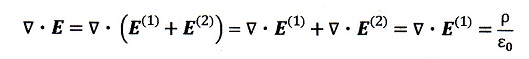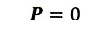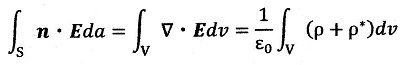電磁気学についての自己の不明と教科書説明の混迷(1)(’13/7)
(前にEH対応とEB対応について書いたものを抹消して全面書き換えしてます)
古い電磁気学の市販教科書を読んでいる中で、私自身、色々と誤解をしていたことに
やっと気が付きました(^_^;)。
一つは電束Dに関してのちょっとした誤解です。
この教科書では、誘電体内の静電界に関する数式による理論展開から
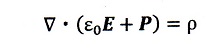
・・・①
という式が導出されています。ここで、

そして、この本では、この式の( )内を
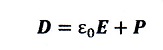
・・・②
とおいて、このDを電気変位(electric displacement)と言うと書かれています。
しかし、私はこの用語が使われている理由がいまいち理解できません(^_^;)。
確かにPは誘電分極による分極ベクトルですから変位というのはわかりますが、ε0E
の物理的意義がわからないのです。
そもそもε0なるものは『真空中の誘電率』と呼称されていますけど、クーロンの実験
結果の式の係数をMKS合理単位系(電磁気関係では現在のSI単位系の大半がこれ
を踏襲している)のときに1/4πε0とおくことで人為的に導入された補正値に過ぎな
い代物じゃないですか?そんな補正値にすぎないε0を電界の強さEにかけたものっ
て一体全体何物?と思うのですが・・・
ネット漁ったんですけど、この用語は出てくるのですが、納得できるような明確な説明を
見付けられませんでした。ま、あまり使われない用語と書いていたサイトもありましたが。
ま、②とおくと、①式から
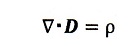
・・・③
となるんですよね。③式が成立しますと、ガウスの発散定理というベクトル演算の公式
から
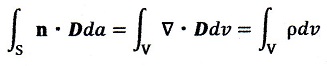
・・・④
となります。Dに対し、Eに対して考えだされた電気力線同様、直交する単位面積当たり
|D|本となる指力線を考えると、④式の最左辺は閉曲面Sから出て行く全線束を意味し、
最右辺は閉曲面S内(体積V)の全電荷を表しています。
ネット調べていましたら、元々、ファラデーは「1個の電荷から力線が1本出てくる」という
イメージを考えていたそうで、丁度この④式はそのイメージに一致しているんですよね。
で、このDを電束(誘電束、dielectric flux)と呼称していて、前述の電気変位よりもこちら
の呼称の方が一般的な気がします。
しかし、以上をよ~く見ていただきたいのです。③、④式はファラデーのイメージを表して
いますが、③式は理論的には②とおくと①式から出てきた結果ですね。言うなればたま
たま、①式と言う結果が数式展開の中で得られたというのが全てなんですよね。
ですから、そもそもの②式の右辺というものが何なのか実に曖昧模糊としているんです。
「つじつま合わせ」の『数学的操作』だけって気がしませんか?
言葉でこの式を説明している本もありますけど、私には後ヅモでちょっと苦しい説明に見
えてあまり理解できませんでした。ε0Eの説明が曖昧だったからです。その本で学んだ
せがれは、単位換算だろうと誤解してました。
ネット見ていたら、やはりこの右辺の意味が理解できなかったとおっしゃっているサイトが
ありました。物理学を専門で学んだ方のサイトですが。
私が何に拘っているかといいますと、前述のように①式は数式展開の結果現れた式だ
というその1点なのです。
この本による①の導出は簡単に言うと、任意の点(x,y,z)における電界Eが

で与えられることを基本にしています。そして、真電荷密度ρによる電位、電界に対し
てはポアソン方程式から
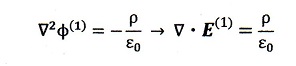
が成立します。
一方、誘電体内では誘電分極による分極電荷密度(体積密度)

により、誘導電位、誘導電界に対して
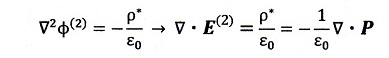
が成立しますので、合成電界は
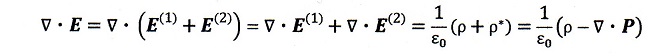
・・・⑤
となり、これから①式が出てくるわけです。繰り返しですが、まさに、①式は純粋に数
式の展開の産物なんですね。
こういう式の展開を見ていたため、実は一つ思い間違いで悩んでしまったことがあり
ます(^_^;)。それは、誘電体外部ではどうなのかという話です。
ここでは、②式で
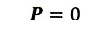
とおいて、
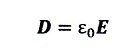
となるんですよね。で、何を思い間違ったかといいますと、この場合は
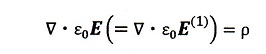
となるからです。この式の真ん中の式は前述の式から出てくるものです。ですから、
何をぼけかましたかといいますと、「えっ?誘電体の外部電界は変化しないの??
そんなばなな・・・」と思ってしまったことです(^_^;)。というのは、ちゃんと、この分極
電荷による電位は誘電体の外にも存在していて、
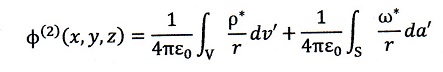
ここで、
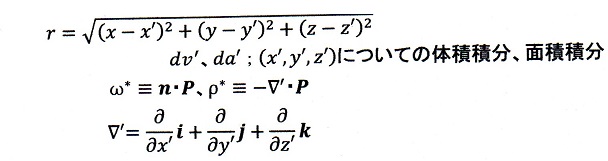
となるから、当然、
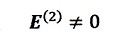
となり、
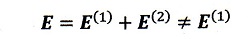
なわけですから・・・。あほでしたね。これらはそれでいいんですよね。
誘電体の外には分極電荷はないので、ラプラス方程式になるんですよね。
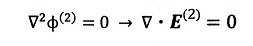
ですから、誘電体の外部では
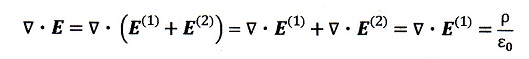
となってめでたく②式で
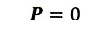
とおいたものと一致するわけです。こんなちょこっとしたこと気が付かずにいて情け
ないですよねぇ(^_^;)。ま、この本は誘電体内だけ強調して説明していて誘電体外に
ついては触れていなかったからと自分に言い訳してます(^_^;)
いずれにしろ、電界Eの指力線である電気力線を考えた時は、⑤式からガウスの電
気線束の式は
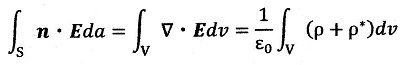
・・・⑥
となり、「美しい体系を好む」(どうも西欧の科学者はキリスト教のバックボーンからか
「宇宙の真理は美しい形であるはず」という強い信念が有る気がします)科学者にとっ
てこの⑥式は「美しくない」んですね。右辺の分母にε0というものがあり、また分極
電荷なるものが入った「見かけの電荷」となっているからです。それに比べて、④式
は右辺にε0も分極電荷も入っていませんから「美しい形」なんですね。
しかし、実際のところ、電気力線もこの電束線も実際に観測されたものではなく、説
明をきれいにするために導入された人為的概念にすぎないんですよね。そして、測
定されるものはいつも真電荷+分極電荷という「みかけの電荷」だけなわけです。
そういうものだと頭でわかっている方は多いと思いますが、教科書にはそういう暴露
は一切なく、あたかも「真理」みたいにたんたんと述べられています。ですから、中
には電力線とか電束線は実在するものではないかと考える(むしろ「仮想的なもの」
だという合理的な根拠はあるのかという疑問を持つ)方だって出てくる気がします。
説明に曖昧さがあるからですよね。
ところで、今の電磁気学の多くの知見はすでに昔のcgs単位系時代になされたもの
で、そのときは、クーロンの法則の係数は1で、電荷の単位はなにかよくわからない
[e.s.u]、磁荷(磁極の強さ)の単位は[e.m.u]なるものだったんですよね。
で、電束というのはいわば指力線の束であり、それを表す次元は本来、本数なわけ
ですから、本質的には無次元のはずではないでしょうか?その指力線の数を単位
面積当たり|D|本と決めた指力線の束が電束の定義なわけです。
ですが、上記のDの定義から今のSI単位系ではDの単位が[C/m2]となりますので、
純数学的に電束の単位は[C]となります。
でも、これだと無次元じゃないですよね?非常に説明不足ではないでしょうか?
結局、電束とか電束密度と概念の次元は「指力線の本数」そのものではなく、その
本数分の電気量ということになりますよね。
しかし、元をただせば、実験現象から、科学者が
目には見えないが「電荷」というものが存在しているはずであると考え
実際の絶対値は不明だが(クーロンの法則の電荷は相対値でのもの)、
現在では単位として[C]と決めて使用している
にすぎないわけです。本当に地球の科学者が思い描いた「電荷」なるものが実在し
ているのかも実は不明なわけで、うまく説明がつくとしているに過ぎないわけです。
多くの科学者が思い込んでなるように「真に解明された」のではなく、「今のところ、
うまくつじつまわせができている」だけに過ぎないのではないでしょうか?
(続く)
目次に戻る
次へ