Maxwellの方程式（1）（’13/3）

前に少し触れましたが、現在、我々が『電磁気学』で学ぶMaxwellの方程式は
1860年台にMaxwellが出したオリジナルなものではなく、数値計算でしか解けな
いため簡単化したかったことと「仮想的なもの」と考えられていたベクトルポテン
シャルを毛嫌いしたHeavisideが1890年台に書き換えた本来は『Maxwell-Heaviside
の方程式』と呼称されるべきと言われるものです。

・・・とまことしやかに書きましたが、恥ずかしながら４０年以上前に工学部で学ん
だ私は当時、そういう事実を習いませんでしたし、ついこの２年ほど前まで全然、
知りませんでした(^_^;)。実践的な工学部と基礎的な理学部では「電磁気学」の内
容に差があって、恐らく理学部の方は私の頃でもそういう事実は御存知だったの
でしょうが・・・

今更、電磁波ってと勉強し直していて、どうも年齢的に頭が固くなったのか元から
か自分でも「理解力が不足している」と感じているように、納得できないというか何
かうまく騙されてしまっているような気がして
（一つは電磁波の周波数って何？という点で。教科書にある平面波の解はexp(jωt)
　がなくても数学的に成立すると思えますから。
　もう一つは、「電場⇒磁場⇒電場・・・」という説明への疑問です）
ネット漁って初めてこのような事実を知ったと言う訳です。
どうもMaxwell-Heaviside方程式は真実を曖昧にしてしまって誤解しやすい悪く言えば
『改ざん』みたいな気がしますね。非線形⇒線形方程式にして解析で解けるようにし
たのですけどねぇ・・・

しかし、Maxwellは自らのオリジナルの式で電磁波を予測していたんですよね。
1890年代初頭にHertzが実証実験で確認するまで言わば学界では無視されていた
という話も目にしました。事実かどうかわかりませんが、当時の学者は彼の理論を
理解できなかったためという話まで目にしました。
要するに、今は電磁波というと決まって1890年台に出された『Maxwell-Heavisideの
方程式』で説明されますけど、極めて数学的能力と物理イメージを描くのが得意で
あったMaxwellのオリジナルな電磁波予測過程とは異なっているということです。
Ｅ，Ｈの式の解ではなくベクトルポテンシャルＡの波動方程式ですよね？
二つも変数項があり、平面波の解でも実際には同時進行しているＥ，Ｈなのに、単に
式の形からＥ⇒Ｈ⇒Ｅ・・・という啓蒙書の類の説明はおかしいと強く感じていた私に
は根本的なところではまだわからないことがあるのですが、このＡだけの式の方が
ずっと理解しやすいのです。これなら球面波というイメージで。

で、これも近年まで知らなかったのですが、量子力学からＡＢ効果としてベクトルポテン
シャルの実在予想が提案され、かんかんがくがくの議論を経てすでに１９８５年に日立の
外村博士の直接実証実験でベクトルポテンシャルの存在が実証されている現在、改めて
元々のオリジナルのMaxwellの方程式で考えるのが「ほんとう」ではないかとネット漁り
しましたら驚くべき話を目にしました。
実際のオリジナルのMaxwellの方程式の全貌とどのような考え方でMaxwellが作ったかを
知ったと言うのが一つの驚きでした。今日の今日まで知らなかった・・・(^_^;)

このサイト（ＰＤＦ文書）に詳しく出ていました

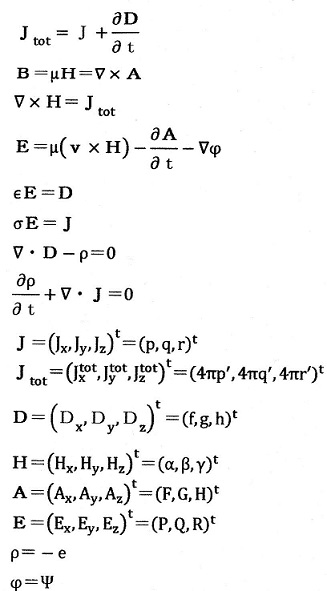
上の８個の式がオリジナルのMaxwellの方程式だそうで、下のような~~３元数~~三次元の数で
表すとこれは２０個の連立方程式となるようです。右上添え字のｔは転置、最右辺はMax-
well自身の使用した表記だそうです。

ポイントはＡの入っている上から２番目の式と４番目の式ですね。
通常は一番上の式がMaxwellのオリジナルの考察（変位電流）と強調されていますが。
私が知らなかったのは上から４番目の式。私が目にしていたものと少し違います。第一項に
μ（ｖ×Ｈ）というのが入っています。これってローレンツ力ですよね。

で、元々ファラデーが実験的に発見したものを式にまとめたものという説明しかなされていな
いのですが、上記サイトによればMaxwellはヘルムホルツの完全流体の渦定理から着想を
得て作り上げたそうです。なぜそういう着想を得たのかまでは書かれていませんが、是非知
りたいです。浅学非才の私には今はすごいなぁとしか言えませんが(^_^;)。ま、だから外村博
士のネットにアップされている論文？で示されていたMaxwellが示したベクトルポテンシャル
をいくつもの渦として描いたものに繋がっているのかなと思いました（恥ずかしながら理学出
身でない私はこのヘルムホルツの完全流体の渦定理は全く知らなくて不案内ですが）。

ところで上記サイトは「Maxwell方程式　ベクトルポテンシャル」でググって見付けたものです
がもっと驚くべき過去の発表理論が紹介されています。
それは前述のMaxwell-Heaviside方程式では出てこないオリジナルのMaxwell方程式の考察
からの発展的な拡張です。ポイントは最初の上記のオリジナルの式は粘性抵抗がないと
した完全流体の渦からの着想の式だということです。
最初に出したのはMaxwell本人だったそうですが、四元数（クォータニオン）を用い、そこで
はなんと例のモノポールの思想がすでに現れていたようです。
ただ、便利なMaxwell-Heaviside方程式が世に出てたため、またもこういうMaxwellの先駆的な
着想は忘れさられていたようです。私は「何かなぁ」って気が強くしています。賛成とか反対と
か言う前に多くの当時の学者は「理解できなかった」のではないかなと。

で、面白かったのは、「エレガントな式」を好んだという話を目にしたことがあるあのDiracが電
場と磁場が非対称なのが気に入らなかったのか、このモノポールの概念を明確に入れた拡
張案を出したようですね。モノポールは未だ未発見ですが、これを入れると対称になるようで
す。

さて、元々、上記サイトの趣旨は「スカラ波」がなんと近年、西欧・ロシアなどの一部の学者の間
で研究されていてその元々の話としてこのオリジナルのMaxwell方程式が不可避であることで
説明がなされています。
私もそうでしたが、スカラ波と聞くと、あの一時話題になった「白装束」の方達を思い浮かべ「とん
でも好き」の私でさえ「とんでも」と思っていたので「えっ？！」と思った次第です。

しかし、どうやら、晩年、「マッドサイエンティスト」の汚名を受け失意のうちに世を去られましたが
日本ではそういう「とんでもさん」扱いを受けてしまっているのに実際は磁束密度の単位や米国
ＩＥＥＥの賞にその名を残している天才「テスラ」（私が「天才」と考えている唯一の人です）が行い、
どうやら軍事秘密で隠されてしまったと言われる業績のうち、成功を修めたとされる「無送電線
送電」実験が見直され理論的な面からこのスカラ波を考える動きがあるそうです。
「テスラ波」と云われているのがこの「スカラ波」すなわち電磁波の縦波というのだそうで・・・。
電磁波の「縦波」はMaxwell-Heaviside方程式からは出てきません（このサイトによると唯一プラズ
マ内という特殊条件では出てくるそうですし、息子に聞いたところでは導波管内でも出てくるそう
ですが・・・）。それは完全流体に対する式を線形式に書き改めたもので横波しか出てこないから
です。だからこそ、オリジナル式に戻って考えないと発展性がないということです。

1990年に４元数（クオータニオン）を拡張したバイクオータニンというのをを用いたブレンデー
レンとワサの拡張で明示的にスカラ波が提起されているそうです。
そしてつい最近の2010年にロシアのポトガイニとザイミドロガという二人が真空を一種の弾性体
と考え線系弾性論のラーメの弾性方程式と言うものを用いて拡張させた論文を出しているそうで
す。驚くことに、ブレンデーレンとワサの拡張は縦波のスカラー波は通常の横波の電磁波と同一
速度ですが、ポトガイニとザイミドロガの拡張ではスカラー波速度＞横波電磁波速度（すなわち
光速）だそうです。

アカデミズム界からこのような論文が出てくるのは極めて興味深いです。

目次に戻る
次へ