熱力学の第二法則について�D（’17/3）(改)

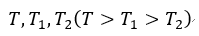
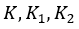
それぞれ温度が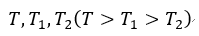

一定のreservoirとしての三つの物体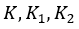

を想定し、次図1の可逆サイクルプロセスを考えるとします。始点(初期状態)を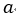

とし、温度を

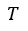とし、図のように体積は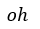

とし、圧力は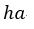

とします。

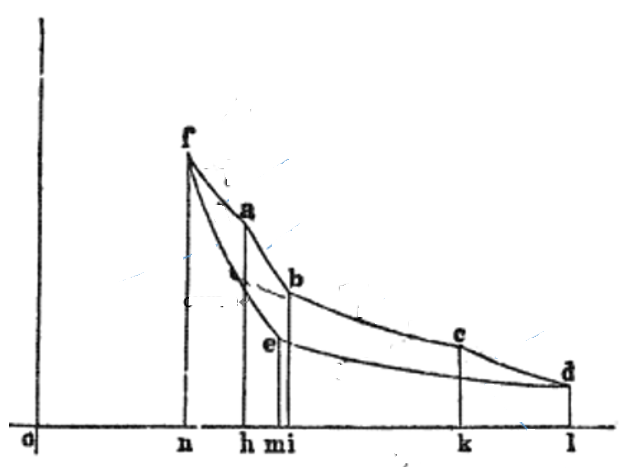図1

最初のプロセス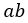

は「断熱膨張」で、このときは温度が低下します。そこで、温度が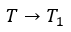

に低下するまで膨張を続けます。したがって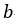

点は温度が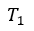

となります。このとき体積は

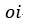圧力は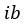

となります。このときの膨張の基準は「温度」であることに留意しましょう。

このときの曲線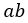

は「等エントロピー曲線(Isentropic curve)」[or「断熱曲線(Adiabatic curve)]

次のプロセス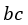

では、可変物体に、温度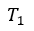

一定の物体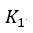

を接触させての膨張であ

り、可変物体の温度は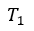

一定に保持されていますので、この曲線は「等温曲線(Isothermal

curve)」となります。この間、可変物体が膨張で失う全ての熱は、物体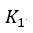

により供給補填され

ています。この時の熱量を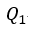

としておきます。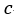

点の温度は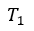

、体積は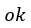

圧力は

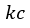となります。

その次のプロセス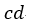

は再び「断熱膨張」です。断熱膨張ですから温度が低下します。そこで

温度が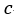

点の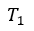

から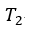

になる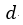

点まで膨張を続けます。図のように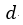

点の体積

は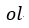

圧力は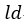

となり そして曲線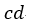

は「等エントロピー曲線(断熱曲線)」となります。

プロセス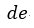

では、可変物体に、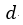

点の温度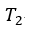

と同じ温度一定の物体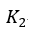

を接触さ

せての圧縮であり、ここでは圧縮によって生ずる全ての熱を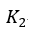

に渡します。そしてその熱量

が、可変物体が物体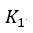

から貰った熱量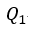

に等しくなるまで温度(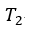

)一定のまま圧縮

します。その最終点が図の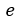

点であり、ここでは温度は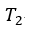

で、体積は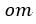

圧力は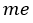

となり、曲線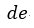

は「等温曲線」となります。

次のプロセス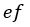

は「断熱圧縮」であり、温度が上昇します。それで、温度が始点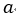

と同じ

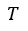になる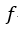

点まで圧縮を続けます。このとき、打ち勝つべき圧力と結果的に熱に変換される

外部仕事は、膨張区間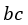

より、この圧縮区間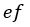

の方が小さいため、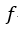

点の体積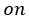

は

元の体積(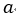

点の体積)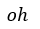

より小さくなり圧力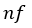

は元の圧力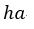

より大きくなります。

Cyclical Processですので、元の状態(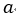

点)に戻す必要がありますが、既に温度は元の温度

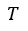になっており、前述からこの最後のプロセス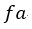

は「等温膨張」であらねばなりません。

そのため、このプロセスでは、可変物体に、温度が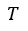

で一定のreservoirとしての物体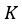

を

接触させ、可変物体はその温度を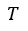

で一定に保つため、物体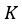

から熱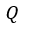

の供給補填を

このプロセス(順方向)において発生する正味の仕事

は図５の閉曲線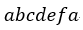

の面積

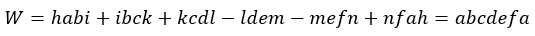・・・(1)

一方、前述のように、プロセス

では可変物体は、物体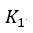

から熱量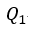

を貰い、プロセス

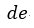では前述のように、物体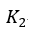

に熱量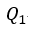

を吐き出しますので、可変物体の熱量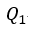

の

出入りは、これらのプロセス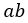

とプロセス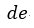

で収支ゼロとなります。

最後のプロセス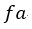

では可変物体に、物体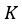

から熱量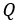

を貰いますが熱の収支を考える

なら、この熱量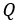

は外部に対いてなされた正味の仕事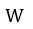

に対応して失う熱量に等しくなけ

ればならないことになります。かくして、クラウジウスは、全プロセスの中でreservoirとしての物体 のうち、二つは終わりにそれぞれ、熱量 を失い、一方、残りは熱量 を 得たと言い、これは「 は、物体 から物体 に渡され、一方、熱量 は完全に 消えた」という表現をしてもよいと述べています。そして、繰り返しますが、「この最後の熱量 は第一基本定理により、外部仕事に変換されていなければならない」と強調しています。 いかがでしょうか？プロセスにおける各点の意味づけ(位置づけ)がより明確化されていて、より論 理的説明がなされていると私は感じましたし、少なくとも、「1サイクルの終了時には初期の状態に 戻る」そして「両方向可能−可逆(reversible)」である"Cycleical Process"における「仕事と熱」の状 態の「物理学的考察」として私にはよく理解できましたので少し長くなりましたが紹介させていただ きました。尚、説明は省略しますが勿論、逆サイクルも可能です。 まとめますと、以上より、熱に関しては次のようになっています。 表1　二つの"transformation" 前述のように、クラウジウスはこの左右の二つを共に"transformation"とし、"Equivalent Transformations(等価変換)"という概念を提示しています。等価のものとして扱おうというわけ で、"§3. On Equivalent Transformations"という節で詳細に述べています。 その"Equivalent Transformations(等価変換)"に彼は「符号(sign)」を次のようにつけるとしています。 　第一の変換(熱⇔仕事)　　　　　　：仕事→熱; 「＋」　　熱→仕事；「−」 　第二の変換(高温⇔低温熱移動)：高温→低温；「＋」　　低温→高温；「−」 従って、可逆サイクルでは、順サイクルと逆サイクルの二つの"equivalent transformation"の符号 は下記となります。 表2　二つの"equivalent transformation"の符号 その上で彼は、"Equivalence-Value(等価値)"というものを導入しています。それには、 　・仕事から熱への変化の値は、生じた熱量に比例しなければならない 　・ただそれがその温度に依存するだけ であることに着目し、変換�@に対して という値を考え 　・温度 から温度 への熱量の移動値は、移動する量に比例しなければならない 　・これ以外は、ただ二つの温度に依存できるのみ であることに着目し、変換�Aに対して という値をを導入しています。 明らかに ・・・(2) となります。 そして、 　全ての可逆プロセスにおいて、起きる二つの変換は大きさが等しく符号が反対であらねば 　ならなくて、その結果、それらの代数和はゼロであるという条件 より、 ・・・(3) (3)式は、二つの熱量を絶対値として、順方向サイクルの場合のものであり、第一項は温度 で熱量 の熱が仕事に変換されることに対応(それゆえ前述の規定に従い"−"がついて います)、第二項は、熱量 が温度 から温度 への熱移動に対応し、前述の規 定により符号は"＋"となっています。 今、逆順を考え、その際、物体 ,物体 そして、それらの間で渡される熱量 は 同じままであるが、温度 の物体 を温度 の物体 で置き換えたプロセスを 考え、そのときの熱量を としますと、このとき逆順ですので、 ・・・(4) となります。(3)(4)式から ・・・(5) となりますが、これより、両サイクルが結合されて一つの連続サイクルを作っている場合、 と の間の二つの熱移動は互いにキャンセルされ、 により放出された熱量 の 仕事への変換と により取り込まれた熱量 の仕事から生じたもののみ残されている ことになります。これより、詳細は省略しますが、考察を進めて、「二つのプロセスは同じ種類 の単一のプロセスに結び付けられる：なぜなら、仕事に変換された熱は第三の物体から引き 出されたものではなく、同じ二つの物体の一方又は他方からのものであるという状況は、その 結果に本質的差異をつくらないから。仕事に変換された熱の温度は付随的なものであり、そ れゆえ、二つの物体のそれ[熱]の温度と同じ値を持つ；その場合、第三の物体はもはや必要 はない。」とし、結論的に ・・・(6) という結果を示しています。 その上で、 ・・・(7) とおいています(原著はここは「温度関数τ」を用いて表記していますが、結局後でτ＝Ｔで あることを彼は証明していますので、本項では最初から温度"Ｔ"を用いました)。 したがって、熱量 を絶対値を示すものとすると、順サイクル時の(3)式は ・・・(8) となります。 彼はこの概念を"the principle of the Equivalence of Transformations"と称し、「熱 力学の第二法則」を次のように表現できると述べています。 　「もし、我々が、任意の他の永久変化を必要とせず、互いにキャンセルしあう二つ 　の変換を等価変換と呼ぶなら、温度 の熱量 の仕事からの生成は、等 　価値(equivalence-value) を有している：温度 から温度 への熱 　の移動は、それにおいて、 がそれにより変換が成し遂げられるプロセスの 　種類とは独立の温度による等価値(equivalence-value) を有 　している そして、彼はこれにより、「我々は、温度 から温度 への熱量の移動は第一の種類 の二重変換すなわち、温度 の熱から仕事への変換とまた、仕事から温度 の熱へ の変換としての同じ等価値(equivalence-value>を持つことを見る。」と述べています。これは、 ・・・(9) となりますので意味は理解できると思います。 そして、彼は「とにかく、我々は等価値の数学的決定において、どんな方法であれ、第一の種類 の二つの相反する変換の結合として起きる全ての熱移動を扱ってよいだろう。」と述べています。 「第一の種類の二つの相反す変換」とは「熱⇔仕事」変換のことです。 その上で、「この規則により、任意の数の両方の種類の変換が起きるが、複雑な任意の周期プロ セス(Cyclical Process)にとって、すべてのこれらの結合した値を表示する数学的表現を導き出す ことはたやすい。」とし、「この目的のため、熱量がreservoirにより放出されるとき、我々はそのど の位置で仕事に変換されるか、何が残るかを最初に問い合わせる必要はない；しかし、代わりに、 周期プロセスにおいて、全て仕事に変換されるとして起きている熱源(heat reservoir)により放 出される全ての熱量と、仕事から生ずるとして取り込まれる全ての熱量を数えればよい。」と述 べています。「reservoirからの熱の放出」＝「熱⇒仕事変換」ですから、前述のように変換の符号 は「負(−)」となります。そこで、「reservoirへの熱の取り込み」＝「仕事⇒熱変換」を「reservoirか らの負の熱量の放出」と解釈することで、熱量を「周期プロセスの間に放出される熱量」とするな ら、各等価値(equivalence-value>は の形で表されるので、周期プロセスにおける変換の 全結合値はこれの合計として表すことができます。 したがって、もし、温度 等の物体 がreservoirとして働き、 が周期プロセスの間に放出される熱量とし、全ての変換の結合値を と すると ・・・(10) となるとしています。そして、「物体の任意の一つの温度が、熱量Q自体の取り込みか任意の他の 原因のいずれかで大きく変化してこの変化が考慮されなければならないなら、そのとき、我々は、 取り込む熱の全ての要素dQに対してその物体がその取り込んだ瞬間に持っている温度を使わな ければならない。このことは、自然に積分に導く」として、 ・・・(11) という式を挙げています。そして、対象が「可逆サイクル」であるなら、それが複雑であっても、そこ で起きる変換は互いにキャンセルされるべきである。」したがってＮ＝０となるとしてその証明をし ています。 その証明として、(7)または(8)式でＮ≠０と仮定し、代数和が０となる部分(分割の変換はペアに分 けられ大きさが等しく符号が反対の二つの変換からなる)と全てが同じ符号である変換からなる部 分に分けるとして、説明しています。詳細は省略しますが、後者についてだけ要約しておきます。 もし、これらの変換が負であるなら、それらは熱から仕事の変換と温度の低い方から高い方への 移動だけが可能(前述の表2参照)であり、もし、温度 の熱量 が仕事に変換されるなら、 その中で温度 の熱量 が仕事から生じ、同時に、他の熱量 が温度 の物体 からより高い温度 の他の物体 に移動される周期的プロセスを逆順で行うだけ で、それにより、熱から仕事への与えられた変換は逆方向になされ、 から への熱の 移動で置き換えられるため、最後には、とにかく消費なしで温度の低い方から高い方への熱の移 動を除いて何も残らないことになり、これは基本原理と矛盾している。したがって、二番目部分の 変換が全て負であるという仮定は誤っていることになります。逆に全て正となるという仮定も逆サ イクルを考えれば同じこととなりこちらも誤っていますので、結局、「可逆サイクル」においては(7), (8)式のＮは０となることになります。したがって、 ・・・（12） となり、結局、"rebersible Cyclical Process"では必ず前項の(6)式である ・・・（13） となるわけです。 以上、前項で述べたreversible Cyclical Processに対して「等価変換(Equivalent of Transformation)」 という概念を入れて提示された再解釈について述べました。 この(13)式に関して、"§7. On the Temperatures of the various quantities of Heat, and the Entropy of the Body."という節で検討していますので、ポイントになるところを要約して引用しておきます。 まず、「物体が一連の条件の変化をなし、最後にその元の状態に戻るような周期プロセスにおい て、可変物体が、もし、熱を受けたり放出するreservoirと繋げられるとき、そのreservoirと同じ温 度であらねばならない」という再三強調してきたことが述べられ、「この条件は、実際、厳密には 満足できない、なぜならば、等しい温度の間には、一般的になんであれ熱の通過はできないから」 とし、「しかし、我々は、少なくとも、それはほとんど満足されていると仮定しているので小さな残っ ている温度差は無視されてよい。」という現在、所謂「準静的状態」と言う概念で述べられているこ とにちょろっと触れています。 そして、 　The expression dQ/τ, if it be understood in the sense just 　given, is the differential of a quantity which depends on the 　condition of the body, and at the same time is fully determined 　as soon as the condition of the body at the moment is known, 　without our needing to know the path by which the body has 　arrived at that condition; for it is only in this case that the 　integral will always become equal to zero as often as the body 　after any given variations returns to its original condition. 　(式dQ/τは、もし、丁度与えられた意味で理解されるなら、物体の条件 　に依存する量の微分であり、同時に、その物体がその条件に到達する 　経路を知っている必要がなく、その瞬間の物体の条件がわかっているや 　否や完全に決定される；なぜなら、それはただ、積分が、任意の与えられ 　た変化がその元の条件に戻る後に物体でしばしばあるいつもゼロに等し 　くなる場合においてのみであるから。) 　(原文のままですので温度関数τが使われています。私の誤記ではありません) と述べ、ギリシャ語から取って「エントロピー」という概念を提案したと述べています。 (ちなみに、そのギリシャ語は だそうです) 最終的には ・・・（14） としています。そして、彼は「熱力学の第二法則」を表す式だとして ・・・（15） を、彼が「熱力学の第一法則」を表す式だとしている�Bの(2)式 ・・・（16） と合わせて重要視しています。 ところで、�Aから始めてここまで綿々と引用紹介して述べて来たものは、"reversible Cyclical Process(可逆周期プロセス)"の場合についてでした。 しかしながら、現実世界を考えた場合、 　(1)この「熱プロセス」に果たして"「可逆プロセス」は存在しているのか？ 　(2)そもそも一つのサイクルでは、終点の状態と始点の状態(温度、体積、 　　圧力)は同じとなるのか？ という疑問を強く感じてしまうのです。私が不案内だけなのかもしれませんが、そのような 実証観測というのはなされていないのではないかと思うのです。 すごく気になったのは、確かにクラウジウスの教科書では、 　CHAPTER X ON NON-RESERSIBLE PROCESS" という章で「不可逆プロセス」の場合について論じています。しかしながら、その論調を見て ますと、どうやら、 　"reversible Cyclical Process"が基本にあって、そこに"non-revesible 　process(不可逆プロセス)"が「混じるとき」の修正という形で済ませている という感を強く感じました。そして、現在の熱力学第二法則はその線上での理論解説になっ ている感がします。 まずは、とにかく、この章から引用紹介したいと思います。クラウジウスは、この章の最初 の"§1. Completion of the Mathematical Expression for the second main Principle"の冒 頭で、 　In the proof of the second main principle, and in the investigations 　connected therewith, it was throughout assumed that all the 　variations are such as to be reversible. We must now consider 　how far the results are altered, when the investigations embrace 　non-reversible processes. 「第二法則の証明とそれとともに関連付けられた研究において、全ての変数 　は可逆であるというような仮定が一貫してなされた。我々は今、その研究 　が不可逆プロセスを擁するとき、その結果がどれくらい変わるかを考えなけ 　ればならない。」 と書いています。 彼は、「不可逆プロセス」の例として、 　(a)物体がその条件、例えば気体の膨張力を変化する力がそれ自身の抵抗 　　を受けなくて、それゆえ、条件の変化の間になされるかもしれない全 　　仕事を行わない 　(b)摩擦や空気抵抗による熱の発生 　(c)電線の抵抗に打ち勝つ電流による熱の発生 　(d)放射・伝導による熱い物体から冷たい物体への直接的な熱経路 を挙げています。これらは、勿論、前項までの"reversible cyclical process"では考慮され てこなかった現象です。そして勿論、これれは「可逆プロセス」ではありません。 しかし考えて見ましょう。私は現実世界で(b)(d)は必然的に伴っている現象だと思うのです。 したがって、「不可逆プロセスがある場合」ではなく、本来、「現実世界を考えた時」ではな いでしょうか？ ま、それはそれとして先に進みます。 彼の論は、前述の「等価変換理論」を元にして、"Cyclical Process"を大前提として、その プロセスが「可逆プロセス」と「不可逆プロセス」からなる場合を想定しています。 Cyclical Porcessが可逆プロセスと不可逆プロセスからなる場合、前者はキャンセルされ てその"Equivalence-value"の代数和はゼロとなりますが、後者はそうはなりません。した がって、(10),(11)式のＮはこの場合、ゼロとなりません。したがって、Ｎは正か負のいずれ かとなるはずです。Ｎが負というのは、"Equivalence-value"が「単独で」負となる(代償無 で負となる)場合でありこれは、前の「変換の符号」で見ると、「温度の低い方⇒温度の高 い方の熱移動」に相当しますが、経験則として、「代償無しでの『温度の低い方⇒温度の 高い方の熱移動』」というのは不可です。したがって、Ｎは負とはなりません。一方、 "Equivalence-value"が「単独で」正となることは、「代償無しでの『温度の高い方⇒低い 方の熱移動』」は自然現象として可能です。前述のような不可逆プロセスの大半は、 「仕事⇒熱」でもありますから、Ｎが正となるのは矛盾なく成立します。したがって、 Cyclical Processが不可逆プロセスを含むとき、 ・・・（17) となるわけです。これを元にクラウジウスは、 　The algebraic sum of all the transformations which occur 　in a cyclical process must always b epositive, or in the 　limit eqaul to zero. 　(周期的プロセスにおいて起きる全ての変換の代数和はいつも正 　または制限付きでゼロに等しくなければならない)(※1) と述べ、更に、 　Uncompensated transformations must always be positive. 　代償の無い変換はいつも正である。(※2) と強調しています。 それゆえ、結局、(17)式より、不可逆プロセスがあるときは必ず ・・・（18) となります。したがって、"reversible cyclical process"と合わせて、 ・・・（19) という「クラウジウスの不等式」と称せられる式がめでたく導出されました。 「物理理論」的には、この説明の方がずっと私にはしっくりきました。 ただ、問題はこの後です。残念ながら、何の説明もなく、この後に、彼は当然のように、 彼が熱力学の第二法則を示す式だとしてきた ・・・（20) の代りに、 ・・・（21) としておくと書かれていました。(21)式の導出については何も書かれていません。 ただ、"§2. Magnitude of the Uncompensated Transformation"という節に少しだけ彼の 考え方が示されていました。下手な和訳だけ引用しておきます。 まず、 　(イ)多くの場合、代償の無い変換(Uncompensated Transformation)の大きさは 　　変換の等価値から直接得られる。 　　・熱量 が摩擦のようなプロセスにより生じ、これが最終的に、温度 　　　の物体に与えられるなら、このように生じた代償の無い変換は、値 を 　　　有している。 　　・熱量 が温度 の物体から温度 の他の物体に伝導により伝 　　　わるとき、代償のない変換は となる。 と述べられています。ここに述べられている「代償のない変換」ですが、「代償のある変 換」とは、「仕事⇔熱変換」と「高温⇔低温熱移動」の両者があって打ち消し合う変換の ことであり、(b)「摩擦による発熱」はいわば「(外部)仕事⇒熱変換」で、これは変換の等 価値の符号は前述では「正」ですから、この「不可逆」プロセスの等価値は のみ であり、「高温⇔低温熱移動」はありません。すなわち、このプロセスは「代償の無い 変換」となります。 一方、(d)「伝導等による直接熱移動」はいわば「高温⇒低温熱移動」であり、これの変 換の等価値の符号は前述では「正」ですから、この「不可逆」プロセスの等価値は となり、「仕事⇔熱変換」はありませんので、「代償の無い変換」と なります。いずれにしろ、これら(b)(d)は一方向プロセスであり「不可逆」ですから、前述 の不可逆のときにこのプロセスでは等価値のキャンセルがなく、かつ「正値」であるた めに(11)式のＮは正値であり、(12)式そして(13)式となることは理解できると思います。 ただ、これは「等価変換」理論における数学的考察でした。そこで、元に戻り、前項の図 ４の任意の"reversible Cyclical Process"がどうなるかを考えておく必要があります。 彼はどう考えたのでしょうか？彼は、 　(ロ)cyclical processは、与えられた物体における、そのいくつかが可逆で他が 　　不可逆である個別の条件の変化からなるかもしれないので、後者の任意の 　　特定の一つが代償の無い変換の全合計を作るのにどれだけ貢献するか知 　　る目的のため、調べたい条件変化[不可逆プロセスのこと]の後、可変物体 　　が、任意の可逆プロセスによってその前の条件にもたらされていると仮定 　　してよい 　(ハ)この方法により、式(11)が全プロセスにおいてと丁度同じように適用できる 　　より小さな(smaller)cyclical processを作る。 と述べています。下手な和訳でわかりにくいかもしれませんが、(ハ)の中に"smaller" cyclical processという語彙があり、私はこれらを次のように解釈しました。 前項の図４は「任意の"Cyclical Process"は無限小カルノーサイクルに分割 できる」という大前提のもとのものでした。勿論、その「無限小カルノーサイクル」は「可 逆(reversible)」です。しかしながら、(b)や(d)の不可逆プロセスがあるときはそうはまい りません。そこで、彼は、その任意の"Cyclical Process"が無限分割された無限小Cyclical Processのうち、不可逆プロセスを(ロ)という条件の"smaller(より小さい)""Cyclical Process"とみなして、「可逆である」「無限小カルノーサイクル」と共に任意のCyclical Processを構成するものとして組み込んだと、そう私は理解したのですが浅学菲才の 私の解釈ですから間違っているかもしれません。 彼は、以上の後で、 　(ニ)物体がこのプロセスの間に取り込んだ熱量と、それらに属する温度を知る 　　なら、負の積分 が起きた代償の無い変換を与える。　しかし、 　　可逆で起きる元の条件はこの和の増大には何も貢献しないので、この式は 　　条件における与えられた変化によって生ずる代償の無い変換を与える。 と述べています。 冗長的でくどいのですが、これまで引用紹介しそれについて述べた私の理解を、私自 身の頭の整理を含めてまとめておこうと思います。 彼は任意の"Cyclical Process"(彼の定義した"Cyclical Processは、Ｐ-Ｖ線図での最 後の点の状態−すなわち一周期における最後の状態−は、最初の点−すなわち一 周期における最初の状態−が同じ−温度、体積、圧力が同じ−cycle process)は前項 では図４で示したような形で無限小の「カルノーサイクル」に分割できるとして積分 を考え、(13)式を導出しました。 一方、本項図1は、その無限小「カルノーサイクル」を�@「仕事⇔熱変換」と�A「温度の高 い方⇔低い方の熱移動」という二つの"trensfromation"に分割して再解釈したものであ り、１：１対応していると考えられます。「等価変換」はそれを元にした理論考察ということ です。 今、等価変換のためのモデル図1の数学的論理は ・・・（22) でしたから、任意の"reversible Cyclical Process"が"infinite small simple revarsible Cycilcal Process"に分割できるなら、それぞれの無限小Cyclical Processで(22)式が成 立しますから、当然ながら上記(12)式となるわけです。しかしながら、そのサイクルに不 可逆プロセスがある場合、そこでは、前述のように、「代償無い変換」だけですから、(22) とはならないわけで、結局(12)式とはならないという事です。で、どうなるかですが、上 記不可逆プロセス例としての(b),(d)は前述の変換の符号に従うなら、共に「正値」とな ります。したがって、この場合は、(17)式となるわけです。 もう少し考察してみると、前述より ・・・（23) ですから、 ・・・（24) となります。仮にあるCyclic Processがあって、それが"reversible Cyclical Process" であるなら、全て"infinite small simple reversible Cyclical Process"の合成とみなすこ とができ、そのときは、 ・・・（25) となります。もしそこに不可逆プロセスがあると(24)式となるわけです。従って、(24)(25) から ・・・（26) となりますので、(21)式となります。 以上は、クラウジウスの１８６５年発行の教科書"Mechanica Theory of Heat"を読んで 私的に解釈したものであり、解釈の妥当性については保留しておきます(大間違いの こんこんちきがあるかもしれません。モチベがある方はそれのPDF(⇒ここをあたって いただければ幸いですm(__)m) ただ、クラウジウスの熱力学の第二法則の「論理」はほぼ理解できたつもりですが、 いくつかの疑問が湧いてきています。それは、 [1]任意の周期サイクルが、本当にみな彼の名付けた"Cyclical Process" 　(すなわち、最終状態と初期状態が完全に同じ−これは、温度、体積、 　圧力がすべて同じということ−)になるのか？ 　⇒これは実験観測で確かめられているのか？ 　　もし彼の言う"Cyclical Process"でない熱機関があるなら、それは 　　この理論のように、"infinite small simple reversible Cyclical process" 　　と上記(ハ)で示された不可逆プロセスに対する仮定的"infinite smaller 　　Cyclical Process"の合成とはならない [2](ハ)(ニ)には根拠があるのか？クラウジウスの"assmption"ではない 　のか？ [3]例えば不可逆プロセスの例として挙げている(b)摩擦熱であるが、こ 　れは現実の熱機関では必然的に存在するものではないのか？そして、 　それは、熱機関における1サイクルにおいて、どこにも必ず存在して 　いるすなわち不可逆プロセスしか現実の熱機関にはないのではない 　のか？(これは「微小状態」だとかマクロ的なものとかそういう問題で 　はなく「物理」的に考えた時の問題です) 熱力学の第二法則について�A〜熱力学の第二法則について�Cで詳しく引用して述 べてきましたように、「カルノーサイクル」についてはその本質的なところをカルノー、 クラウジウスの著書からほぼ理解できたと思っていますし、その本質的なところでこ れが理想的最高効率熱サイクルであるということも自然と理解できたつもりです。 しかしながら、彼が創設した「エントロピー」の存在に疑問が生じてきました。 前は、ウェブテキストに多々ある(26)式の証明に疑念を感じていたのですが、クラ ウジウスの考え方は異なっていました(私はそう解釈しました)が、どう説明しようと それとは別に、上記[1]〜[3]への疑念が払しょくできなゆえです。 くどいのですが、クラウジウスは、(13)式が任意のCyclical Processで成立するとき (14式)とおくと、 は完全微分可能な状態変数になるとして、この に「エントロピー」という名前を付けました。そしてこれも彼が最初に使用する ようになったと主張している記号 −彼はこれを「エネルギー」と称しました− と共に、後者は熱力学の第一法則、前者は熱力学の第二法則を構成する重要な 「状態量」とみなして再三強調しています。 例えば、CHAPTER �\"DETERMINATION OF ENERGY AND ENTROPY の§1. General Equationの冒頭には、 　In former chapters we have repeatedly spoken of the 　Energy and Entropy of a body as being two magnitudes 　of great importance in the Science of Heat, which are 　determined by the condition of the body at the moment, 　without its being necessary to know the way in which 　the body has come its this condition. 　(前までの章で我々は、繰り返し、熱科学における大変重要な 　二つの大きささとして、物体がこの条件に入った方法を知る 　必要なくその瞬間の物体の条件によって決定される物体のエ 　ネルギーとエントロピーについて話して来た。) と書いています。ですから、クラウジウスの不等式の元になった"non-reversible process"はその延長上で論じられていることは間違いないでしょう。 大変失礼なことを言ってしまうと、クラウジウスは自分が見出して命名した「エント ロピー」に魅せられてしまったのではないかと思うのです。そして、現代の科学者も それに私のような疑念を抱くどころか、２０世紀に現れたボルツマンによる「統計力 学的エントロピー」そして更には情報工学の専門家がAnalogyから提示した「情報エ ントロピー」によりすっかり魅せられてしまっている感がします。しかしながら、再三 強調してきましたが、「統計力学的エントロピー」は「熱力学の第二法則」から「論理 的」に導出されたものではなく、ボルツマンが数式からのひらめきで構築したものだ ということです。ボルツマン定数なるものをつけて熱力学との数式的な辻褄わせを してはいますが。 しかしながら、クラウジウスが代表する式だと強調している、熱力学の第一法則を 表す式(16)は「等式」ですが、第二法則を表す式(21)は不等式です。 そして、重要なことは、(16)式は、例えば「Ｃ言語」の「＝＝」に相当するもので「右 辺と左辺が等しい」ことを意味しているのに対し、(15)式の「＝」は、例えば「Ｃ言語」 の「＝」に相当するもので、「右辺を左辺に入れる」に近い「右辺を左辺とおく」という いわば「定義」となるのです。なぜなら、その他のところでdSは定義されていません から。そして、クラウジウスのこの教科書では、最初にそれが出てくる第�V章〜第九 章まで、一貫して"reservsible Cyclical Process"を前提にした論議であるということ に留意すべきです。すなわち、dSが入っている等式は悉く、(15)式がベースになって いま 私はクラウジウスが提示した"reversible Cyclical Process"の理論は論理的で合理 的であると考えています。しかしながら、私は現実の熱機関は"non-reversible Cyclical Process"であると考えます。したがって、私は実際には、彼がnon reversible processとして第十章の§1、§2で論じた説明とは違うのではないかと思うのです。 彼が言うように、任意のCyclical Processでどこに「不可逆プロセス(non-reversible process)」があろうと彼の理論展開の中では問題になりません。しかし、全プロセス が「不可逆プロセス」であったら、そもそも現実世界では(13)式そのものが存在しな いことになります。そして、(13)式が現実世界では存在しなとしたら、(14)式のdSは 物理的意味のある物ではなくなってしまわないでしょうか？要するに、あくまで理想 的な"reversible Cyclical Process"の世界でだけのものではないかと・・・ 私に言わせていただくなら、前述の疑念についての納得できる合理的説明がなされ ていない・こなかったのではないかと思うのです。 我ながら本当にしつこいのですが、実際の熱機関との対比でこれまで綿々と書いて きた、カルノーそしてクラウジウスの理論におけるポイントと考えた記述はほぼ紹介 してきたと思いますので、以下それは繰り返しません(�A〜本項までを再読いただけ れば幸いですm(__)m)が最低限のところだけはかいつまんでみていこうと思います。 彼の「等価原理」における"reversible simple Cycrical Process"の説明では、順サイ クルで説明すると、温度Ｔのresirvoir"Ｋ"から可変物体に供給されて可変物体の温 度をＴ一定に保つ熱量Ｑは外部に対してなされる仕事に変換され、温度Ｔ1のreser- voir"K1"から可変物体の温度をＴ1一定に保つために可変物体に供給される熱量 Ｑ1は、可変物体から可変物体の温度をＴ2一定に保つための温度T2のreservoir "K2"に吐き出される(すなわち、熱量Ｑ1はＫ1⇒Ｋ2に移動される)という説明でした (注：Ｔ＞Ｔ1＞Ｔ2）。もし、順サイクルで、Ｋ＝Ｋ1、Ｔ＝Ｔ1とし、温度Ｔ1のreservoir "K1"から可変物体に供給される熱量をＱ1、可変物体から温度Ｔ2のreservoir"Ｋ2" に渡される熱量をＱ2とするなら、クラウジウスの説明でＱ1＝Ｑ2+Ｑとなるというこ とを前項で述べました。 要するに、"reversible simple Cyclical Process"としては「余分なムダな熱量」とい うのはなかったのです。当然ながらこれ以上の効率はないことは論理的にわかる と思います。しかるに、例えばエンジンで水冷・空冷という冷却が施されているの はどうしてでしょうか？私は当初、上記のreservoir"K2"("Cold Body")をそれだと 思い違いしていました。あの理論説明によれば、Ｔ1とＴ2の差は微小でよい(温度 差があればよい)ということでした。クラウジウスはreservoir"K2"を"colder body" (より冷たい物体)と称しています。逆にreservoir"K1"を"hotter body"または "Warmer Body"と称しています。あくまで「比較して『温度が高い方』『温度が低 い』としているだけです)。結局、現実の熱機関においては、ちょこっとの修正では 済まない不可逆プロセスが熱プロセスでは大きな存在であり、全体の熱的バラン スの中で、余分に出てくる熱量や直接伝導・放射の影響による温度上昇を抑える ために水冷とか空冷とかいう措置がとられているのではないかと思うわけです。 単純なピストン上下運動の機関において位置的な周期はありますから、体積は終 点と始点で同じとなると思います。しかしながら、温度については上記のような 余分な措置を施しており、本当に毎回同じ状態に戻っているか不明ですし、戻る としてもそれはあのようなreversible simple cycical processで戻るわけではない はずです。 「熱力学は微小変化の理想的世界を扱っている」というような説明を目にしたこと があります。確かに、「準静的過程」などというのはそういう世界での話でしょうし、 それよりもなによりも"reversible Cyclical Process"自体がそうでしょう。 しかしながら、それを現実世界の「熱機関」の「熱プロセス」に適用するのをクラ ウジウスや現代の科学者の説明のような「修正」だけで適用できるのかという疑 問が強く私の中で湧いてきています。そして、その中で「エントロピー」というのは 本当に存在するものなのかという疑問も湧いてきているのです。私がなんとか納 得できたのは、"reversible Cyclical Process"に対する理論及びクラウジウスの 説明における「クラウジウスの不等式」までです。(26)式は納得できていません。 従って(26)でｄＱ＝０として出てくる「エントロピー増大則」なるものを自然の摂理 などという主張には猶更納得できていません。既に書いてきましたが、百歩譲っ て(26)式を認めるとしても、宇宙系は「孤立系」だからと何の実証観測もなく決め つけてｄＱ＝０だからｄＳ＞０だという説明は全く納得できていません。 残念ながら、オリジナルの教科書を読みましたけど、私の違和感を解消してくれ るような合理的説明はありませんでした。ま、熱力学に関してはこれで終わりと します。(この項終わり) ---------------------------------------------------------------------- (追記) 気にしていたことを書き忘れていましたので補足しておきます。 大抵のテキストでは、クラウジウスの不等式の導出において、任意の周期プロセ スに対し、往路＝不可逆プロセス、復路＝可逆プロセスとして求めています。 しかるに、そう考えてよいという根拠は皆書かれておらず、何か当然のように示さ れています。ですから、最初にそれを目にした時、私はなぜそうできるのか？とい う疑問にさいなされてしまいました。 しかし、そもそも熱力学の第二法則を体系化し、この不等式やエントロピーの概念 を提起したクラウジウスの上記で示して来た説明とは一つの乖離を感じました。 「積分」を見ているということは、マクロとしての任意の「周期サイクル」ですが、彼 が「不可逆プロセス」として考察しているのは、"infinite small(無限小) cyclical process"であることは上記(ハ)の中にある"smaller cyclical process"という言葉か ら明白です。 そもそも、クラウジウスは、任意の"reversible Cyclical Process(可逆周期プロセス)" は"infinite small revbersible Cyclical Process"(すなわち微小カルノーサイクル)の 合成として数学的に体系化しています(⇒前項参照)。その分割図を前項図4に示 しました。有限すなわちマクロでの任意の"reversible Cyclical Process(可逆周期 プロセス)"はその図のような形での積分を考えたという事です。そして彼はその理 想的微小カルノーサイクルに対して視点を変えた再解釈として、前述の図1の形を 考え、"infinite small revbersible Cyclical Process"ではそれぞれで(22)式が成立 するとみたわけですから、いわば、 ・・・（27) を、それぞれ無限小可逆周期プロセスのものとして、(12)式という積分を考えたの です。正負の値を持つ微小熱量(例えば、仕事をする気体などの可変物体に熱が 伝わる方向を正とする)を考えるなら、一つの無限小可逆周期プロセスにおいて ・・・（28) 　--------　　　----------------- 　　　↑　　　　　　　　　　　　↑ 　　熱⇒仕事　　　　　　　熱移動 と考えると当然(12)となるというわけです。 ですから、彼の言う「不可逆プロセス」というのは、その「無限小可逆周期プ ロセス」において、本来の熱機関としての「仕事」にならないもの−例えば、摩擦に よる発熱の場合は(27)式で見れば第一項の のみがあるプロセス、直接 高温 部から低温 部に熱量 が伝導・放射で伝わる場合は (27)式で見れば、第二項・第三項の のみがある場合と 考えているわけです。したがって、本質的には、一方的(不可逆)であり「周期サイ クル」とはならないのですが、上記(ロ)としたのは、恐らく、"infinite small(無限小) を考えているゆえ、近似的にそうみなしていいのだとしたのだろうと思うのです。 それが"Smaller"という語彙に現れていると思います。"infinite reversible Cyclical Process"より更に小さい＝更に極小のものとして前項の図4に組み込んだという ことです。ですから、(ロ)という仮定が真に妥当かどうかは別として、この説明なら 論理的であろうと私は納得できました。一方、多くのテキストにあるマクロとしての 任意の周期プロセスを考えてその往路を不可逆プロセスとし復路を可逆プロセス で結ぶという考え方には、根拠となる合理性・論理性が私には感じられません。 すなわちそこにおける「可逆プロセス」「不可逆プロセス」の概念が曖昧に見える のです。そもそも、(27)式⇒(12)式と考えるなら、「積分」は文字通り であ 「周回積分」としての とはちょっと違うのではないかと思うのですが何か 勘違いしているのでしょうか？「仕事」であるなら、 ですが。 周期プロセスをＰ-Ｖ線図で見ているのですけど、クラウジウスが"Ciclical Process" と名付けたものは、どちら周りにおいても必ず同じ経路を辿り、始点(最初の状態) と終点(最後の状態)において、体積・圧力だけでなく、「温度」も同じにならなけれ ばならないということです。そして、どういうときにそうなるのかということはそもそも 議論の対象などにはしてないのです。 もっとも、クラウジウスの説明を見ていますと、何か、一般の熱サイクルの大半が infinite small "reversible" Cyclical Processからなっていて一部にだけ「不可逆プ ロセス」があるということが基本になっている感がしますけど、現実は「不可逆プロ セスばかり」ではないのかというのが前述の私の最大の疑問です。 　('17/3) 目次に戻る