
 |
| Rudolf Clausius |
 |
| James Prescott Joule |
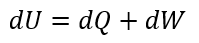 | ・・・(1) |
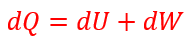 | ・・・(2) |
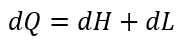 | ・・・(3) |
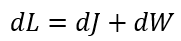 | ・・・(4) |
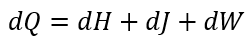 | ・・・(5) |
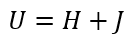 | ・・・(6) |
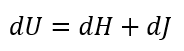 | ・・・(7) |
| 方法には依存しない」ゆえに、有限値として得られる積分値は、初期値(initial value)を | 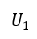 | と |
| 最終値(final value)を | 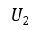 | とすると |
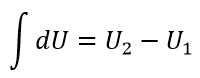 | ・・・(8) |
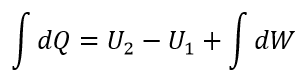 | ・・・(9) |
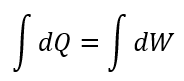 | ・・・(10) |
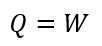 | ・・・(11) |
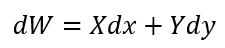 | ・・・(12) |
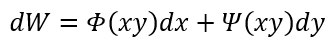 | ・・・(13) |
| となるとします。そのとき、関数 | 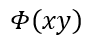 | と | 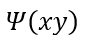 | の性質に従い二つの区分があり |
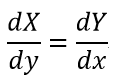 | ・・・(14) |
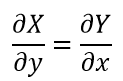 | ・・・(14') |
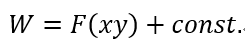 | ・・・(15) |
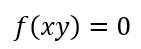 | ・・・(16) |
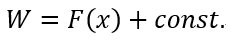 | ・・・(17) |
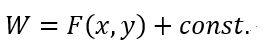 | ・・・(18) |
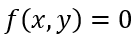 | ・・・(19) |
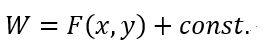 | ・・・(20) |
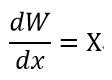 | ・・・(21a) |
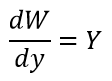 | ・・・(21b) |
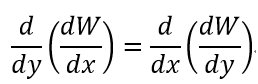 | ・・・(22) |
| 「このように、我々は、量Wに関連して描かれるべき区別が、差 | 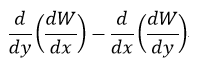 |
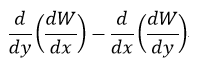 | がゼロに等しい時はその1となりそのまま積分可能であるが、ゼロ |