 |
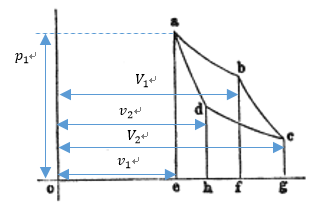
| 図1 |
| まずは可変物体の膨張プロセス | 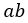 | 、 | 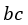 | プロセスを考える。 |
| 可変物体のに初期条件として、始点 | 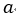 | に圧力 | 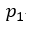 | 体積 | 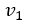 | を与えることとする。そして、 |
| この始点 | 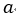 | から、可変物体に、"resevoir"として働く温度 | 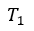 | で一定 の物体 | 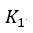 | を接触させ |
| 可変物体の体積を | 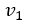 | から | 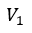 | まで 膨張させる。膨張プロセスなので、断熱状態なら温度は |
| 下がるが、温度 | 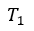 | 一定の"reservoir"に接触させているため、可変物体の温度は低下せず | 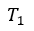
|
| に保たれる。したがって、始点 | 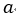 | から、体積が | 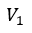 | と なる点 | 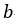 | までの曲線 | 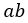 | は |
| 「等温曲線(Isothermal curve)」となる。この間、可変物体は温度 | 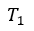 | を維持するため、接触 |
| させている物体 | 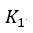 | から熱の供給を受けている。 |
| 次に、 | 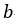 | 点で、可変物体から物体 | 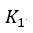 | を切り離して そのまま、体積が | 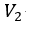 | になる | 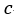 | 点ま |
| で膨張させる。このプロセスでは可変物体の温度低下が起き、温度は |
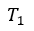 | から | 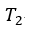 | まで低下 |
| する。すなわち、 | 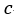 | 点の温度は | 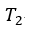 | である。この時の曲線 | 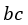 | は「等エントロピー曲線 |
| 可変物体は断熱膨張プロセス | 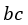 | により |
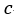 | 点で体積 | 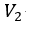 | 、温度 |
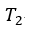 | となっているので、 |
| まず、この | 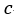 | 点から可変物体を温度が | 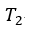 | 一定の"reservoir"として働く物体 | 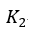 | を接触さ |
| せて体積が | 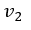 | となる | 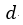 | 点まで圧縮する。 断熱状態なら圧縮では温度が上昇してしまうが、 |
| "reservoir"としての温度が自身 | 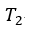 | 一定を維持させている物体 |
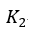 | を接触させているのでプ |
| ロセス | 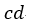 | は「等温曲線(Isothermal curve)」となる。 |
| 最後に、体積が | 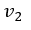 | 、温度が | 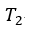 | の | 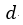 | 点で物体 | 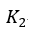 | を切り離し、引き続き体積が初期の |
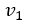 | に戻るまで圧縮を続ける。この時、温度が初期の | 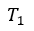
| に戻れば、始点 | 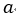 | に戻ることに |
| なる。このプロセスの曲線 | 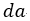 | は「等エントロピー曲線(Isentropic curve) (断熱曲線 |

|
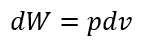 | ・・・(1) |
| したがって、可変物体(気体など)体積 | 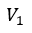 | から体積 | 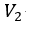 | まで 膨張する場合、外部に対してな |
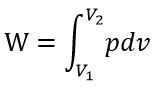 | ・・・(2) |
| これより、膨張プロセスにおいては、プロセス | 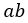 | のときの外部に対する仕事は図1では四角 |
| 形 | 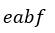 | となり、プロセス | 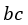 | のときの外部に対する仕事は図1では四角形 | 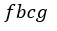 | となり |
| ます。一方、圧縮プロセスにおいては、プロセス | 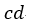 | のときの外部からなされる仕事は図1で |
| は四角形 | 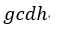 | となり、プロセス | 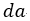 | のときの外部からなされる仕事は図1では四角形 |
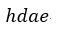 | となります。後者の二つの量は圧縮中の低い温度ゆえに前者の二つより小さくなります。 |
| したがって、前者から後者を差し引いた分である四角形 | 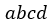 | は外部仕事の過多分となり、 |
| このCyclical Processにより外部になされた正味の仕事 | 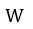 | となります。 |
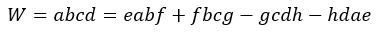 | ・・・(3) |
| このように、このCyclical Processにより得られた仕事量 | 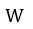 | は 前項③(11)式より、値において |
| はその生成に必要な熱量 | 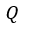 | と等しくなります。 |
| 今、可変物体は、物体 | 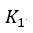 | と繋がれている膨張プロセス | 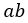 | の間、物体 | 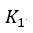 | から熱量 | 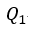 |
| を得ます。一方、 | 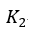 | と繋がれている圧縮プロセス | 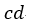 | の間、可変物体は、物体 | 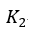 | に熱 |
| 量 | 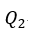 | をを与えます。膨張プロセス | 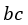 | と圧縮プロセス | 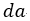 | の間は、可変物体は熱を与え |
| ることも貰うこともありません。今、全cyclical processにおいて、熱量 | 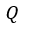 | は、前述のようになさ |
| れる正味の外部方向の仕事が吸収しますので、物体 | 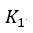 | より可変物体が受け取る熱量 | 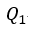 |
| は、可変物体が、物体 | 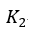 | に与える熱量 | 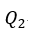 | より大きくなります。 |
| したがって、その差 | 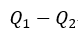 | は | 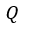 | に等しく |
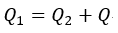 | ・・・(4) |
| これより、可変物体が物体 | 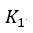 | から引き出された熱量 | 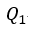 | の中で二つの部分に分離され、そ |
| の一つ | 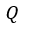 | は仕事に変換され、一方、他の | 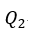 | は物体 | 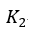 | に熱を返していることになります。 |
 |

|
| 逆順も始点は、 | 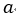 | で、そこでは体積は | 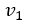 | 、温度は | 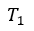 | とします。 |
| まず、最初に、可変物体には熱は与えられず、体積 | 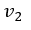 | となる | 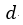 | 点まで膨張させます。この |
| プロセス | 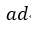 | の曲線は「等エントロピー曲線(Isentropic cuve)」となります。このとき、可変物体 |
| の温度は下がりますので、それは | 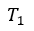 | から | 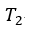 | に低下したとします。すなわち、 | 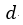 | 点の温 |
| 度は | 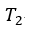 | となります。次にここから可変物体に温度 | 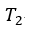 | 一定の物体 | 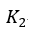 | を接触させながら |
| 可変物体の温度を一定の | 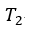 | に保ちながら体積 | 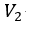 | の | 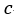 | 点まで膨張させます。彼の説明 |
| では、このプロセス | 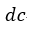 | では、可変物体が物体 | 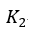 | から熱を引き出している間という言い方 |
| をしています。ちなみに、このプロセス | 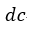 | は「等温曲線(Isothermal curve)」となります。 |
| それから、次に | 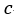 | 点から圧縮プロセスに入り、まず、断熱状態(熱の出入り無し)で体積 | 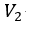 | か |
| ら体積 | 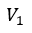 | の | 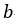 | 点まで可変物体を圧縮します。このとき、可変物体の温度は | 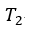 | から | 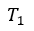
|
| に上昇したとします。このプロセス | 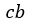 | は「等エントロピー曲線(Isentropic curve)」となります。 |
| 最後に、 | 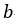 | 点から、可変物体に、温度 | 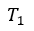 | 一定の物体 | 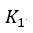 | を接触させながら、元の体積 |
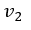 | の元の | 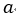 | 点まで圧縮を続けます。このとき、彼の説明では、可変物体は物体 | 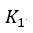 | に熱 |
| を与えるという表現を使っています。この最後のプロセス | 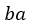 | は「等温曲線(Isothermal curve)」 |
| プロセス | 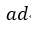 | に対する仕事量(図1で四角形 | 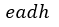 | )とプロセス | 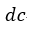 | に対する仕事量(図1で |
| 四角形 | 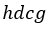 | )はなされた仕事または正のものであり、プロセス | 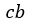 | に対する仕事量(図1で |
| 四角形 | 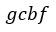 | )とプロセス | 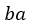 | に対する仕事量(図1で四角形 | 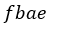 | )は吸収される仕事ま |
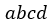 | この場合、吸収される仕事となります。 |
| 可変物体は物体 | 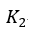 | から熱量 | 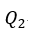 | を引き出し、物体 | 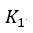 | に熱量 | 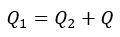 | を与 |
| えます。これは前述の(3)式と同じ形ですね。 | 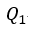 | が構成されている二つの部分のうち、 | 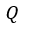 |
| は吸収された仕事に相当し、他の部分 | 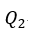 | は、物体 | 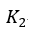 | から物体 | 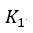 | に熱として渡され |

|
| 順サイクルでは、「等温曲線」プロセス | 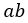 | では、「物体 | 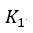 | が可変物体に熱を与え」、「等温 |
| 曲線」プロセス | 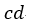 | では、「可変物体が、物体 | 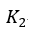 | に熱を与える」としているのに対し、逆サイ |
| クルでは、「等温曲線」プロセス | 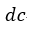 | では、「物体 | 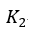 | が可変物体に熱を与え」、「等温曲線」 |
| プロセス | 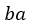 | では、「可変物体が、物体 | 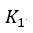 | に熱を与える」という表現になっています。 |
| すなわち、順サイクルと逆サイクルでは、可変物体(気体など)と物体 | 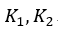 | の間の熱流の方 |

|
| ということです。可変物体と物体 | 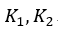 | を接触させるときに温度差があると、可変物体の温度 |
| 商 | 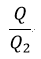 | は可変物体の性質には独立であるので、それはただ、reservoirとして働く二つの物体 |
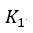 | と | 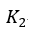 | の温度のみに依存することができるとし、更にその時 | 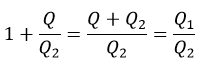 |
| であるので、商 | 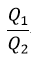 | もreservoirとして働く二つの物体 | 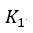 | と | 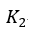 | の温度 | 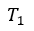 | と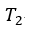 | のみ |
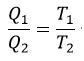 | ・・・(5) |
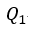 | は、高温(温度 | 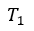 | )側のreservoirとしての物体 | 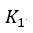 | から可変物体に供給される(放出さ |
| れる)(逆サイクルのときは可変物体から流入する)熱量、 | 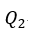 | は、低温(温度 | 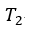 | )側のreservoir |
| としての物体 | 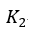 | に可変物体から流入する(逆サイクルでは可変物体に供給する)熱量です。 |
| この熱量 | 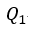 | と | 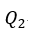 | はreservoirから流出する・reservoirに流入するという方向性があります |
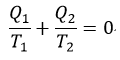 | ・・・(6) |
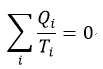 | ・・・(7) |
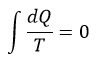 | ・・・(8) |
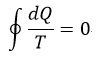 | ・・・(9) |
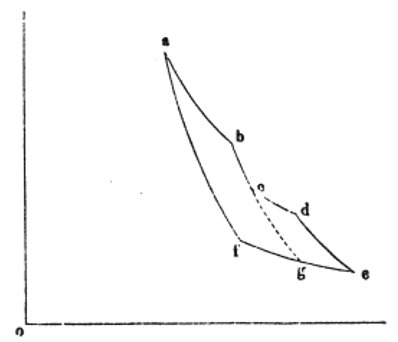 |
| 図2 |
| 曲線 | 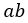 | は一定温度 | 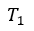 | での膨張を表します(等温曲線)。 |
| 曲線 | 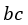 | は熱の出入りの無い膨張でその間、温度は | 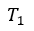 | から | 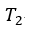 | に低下します(等エントロ |
| 曲線 | 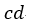 | は一定温度 | 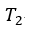 | での膨張を表します(等温曲線)。 |
| 曲線 | 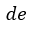 | は熱の出入りの無い膨張でその間、温度は | 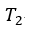 | から | 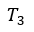 | に低下します(等エントロ |
| 曲線 | 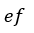 | は一定温度 | 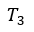 | での圧縮を表します(等温曲線)。 |
| 曲線 | 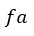 | は熱の出入りの無い膨張でその間、温度は | 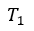 | から | 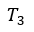 | まで上昇します(等エント |
| 膨張 | 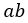 | と | 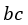 | では、可変物体は正の熱量 | 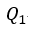 | 、 | 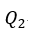 | で起き、圧縮 | 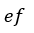 | は負の熱量 |
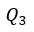 | でおきます。 |
| 今、図に示すように、等エントロピー曲線 | 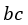 | の延長上に破線で示した等エントロピー曲線 | 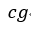
|
| を仮定します。その結果、全プロセスは、単純プロセス | 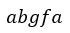 | と | 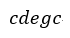 | に分割されます。 |
| 圧縮 | 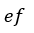 | の間に取り込まれる負の熱量 | 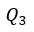 | を、第一の部分は圧縮 | 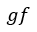 | の区間で、第二の |
| 部分は圧縮 | 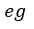 | の区間で取り込まれる二つの部分 | 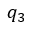 | と | 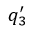 | に分割されると仮定します。 |
| このとき、 | 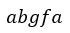 | に対しては |
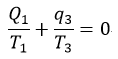 | ・・・(10) |
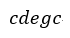 | に対しては |
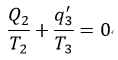 | ・・・(11) |
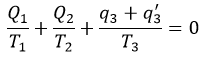 | ・・・(12) |
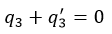 | ・・・(13) |
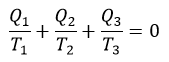 | ・・・(14) |
| いずれにしろ、結果として | 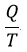 | という形の分数の代数和となっていますが、留意すべきことは、 |
| この分数式において、熱量 | 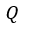 | は温度 | 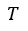 | のreservoirから流出・流入する熱量であるという |
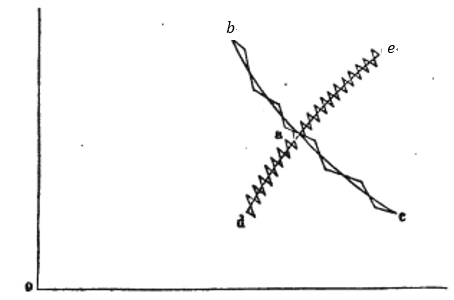 |
| 図3 |
| 動は図3の場合、 | 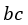 | または | 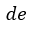 | のコースにに沿って、交互の等温要素と等エントロピー要 |
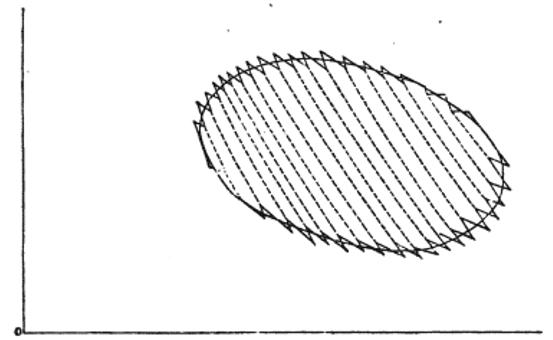 |
| 図4 |
| 積を合計したものであることは間違いなく、また、図3の考え方を発展させれば、(8)式は、温度 | 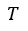
|
| の無限小分割reservoirから流入出する(したがって正負の符号を持つ)熱量 | 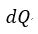 | に対しての商 |
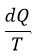 | の代数和と考えてよいと思います。くどいですが、クラウジウスのテキストにそこまでくど |
| とみなし、その「等温」にするreservoirとしたものです。したがって、(8)式の積分項 | 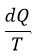 | における |
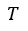 | と | 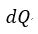 | は1無限小分割reservoirに対するものであり、 | 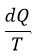 | の形で刻々変化していくもの |