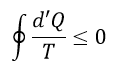
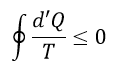 | ・・・(1) |
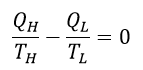 | ・・・(2) |
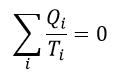 | ・・・(3) |
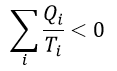 | ・・・(4) |
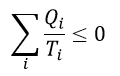 | ・・・(5) |
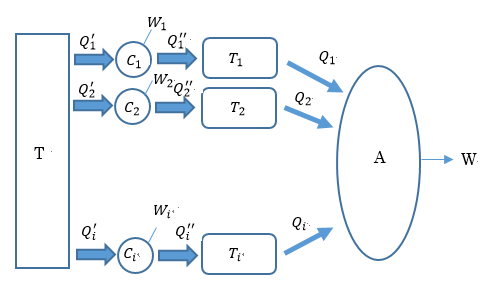
|
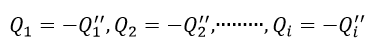 | ・・・(6) |
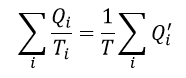 | ・・・(7) |
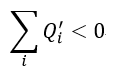 | ・・・(8) |
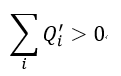
|
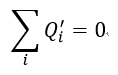 | ・・・(9) |
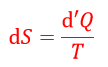 | ・・・(10) |
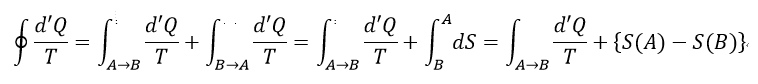 | ・・・(11) |
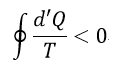 | ・・・(12) |
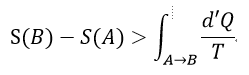 | ・・・(13) |
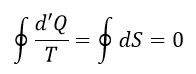 | ・・・(14) |
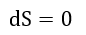 | ・・・(15) |
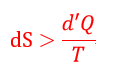 | ・・・(16) |
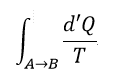
|
|
|
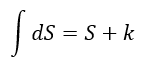 | ・・・(17) |
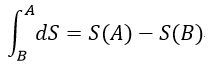 | ・・・(18) |
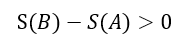 | ・・・(19) |
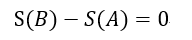 | ・・・(20) |
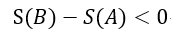 | ・・・(21) |
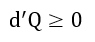 | ・・・(22) |
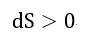 | ・・・(23) |
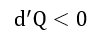 | ・・・(23) |
| 断熱系( | 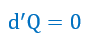 | )において、不可逆過程があるなら、 |
 | ・・・(24) |
| 断熱系( | 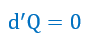 | )においては、 |
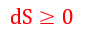 | ・・・(25) |
 | すなわち「エントロピー増大」は自然の要請ではない |
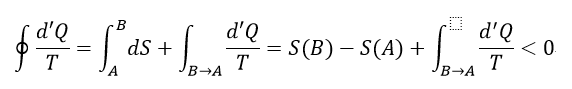 | ・・・(26) |
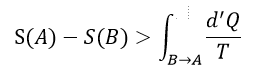 | ・・・(27) |
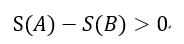 | ・・・(28) |
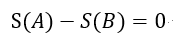 | ・・・(29) |
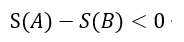 | ・・・(30) |
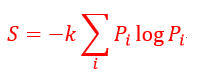 | ・・・(19) |
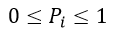 | ・・・(20) |
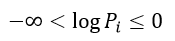 | ・・・(21) |
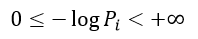 | ・・・(22) |
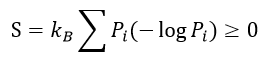 | ・・・(23) |
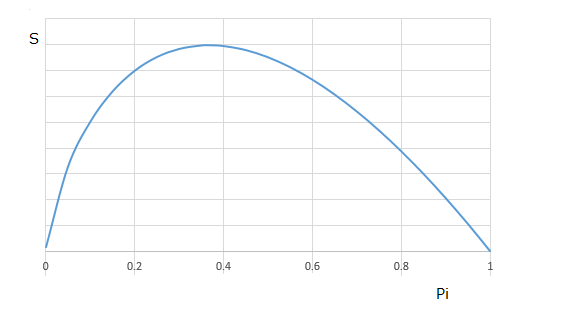
|
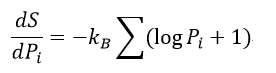 | ・・・(24) |
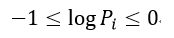 | ・・・(25) |
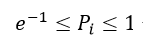 | ・・・(26) |
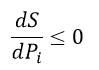 | ・・・(27) |
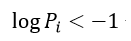 | ・・・(28) |
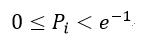 | ・・・(29) |
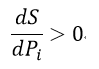 | ・・・(30) |
| 確率が | 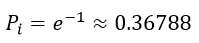 | まで小さくなっていくとエントロピーSは確かに増加して |