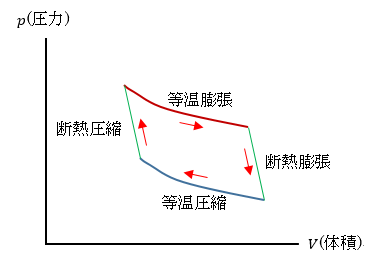

|
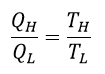 | ・・・(1) |
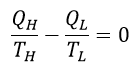 | ・・・(2) |
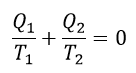 | ・・・(3) |
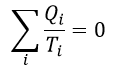 | ・・・(4) |
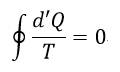 | ・・・(5) |
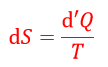 | ・・・(6) |
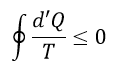 | ・・・(7) |
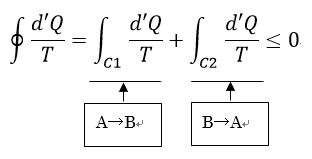 | ・・・(8) |
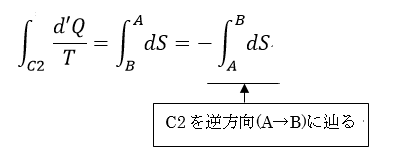 | ・・・(9) |
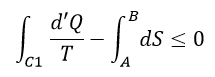 | ・・・(10) |
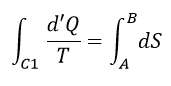 | ・・・(11) |
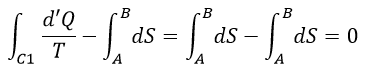 | ・・・(12) |
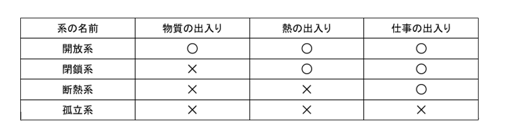
| 尚、この場合は、常に(6)式が成立し、 | 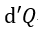 | が正(熱が外界から系内に入り |
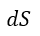 | はそれに従って、正(エントロピーは増大する)・負(エントロピーは |
| (10)式の等号"="は決して | 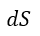 | が0だからではありません。 |
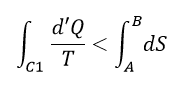 | ・・・(13) |
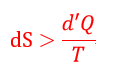 | ・・・(14) |
| のときです。そして、断熱系では、 | 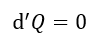 | ですので、 |
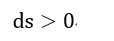 | ・・・(15) |
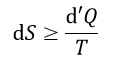 | ・・・(16) |
 | ・・・(17) |
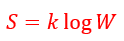 | ・・・(18) |
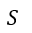 | :エントロピー |
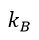 | :ボルツマン定数 |
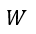 | :微視的状態の数 |
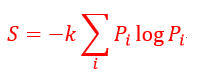 | ・・・(19) |
|
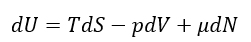 | ・・・(20) |