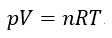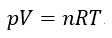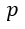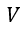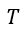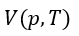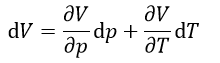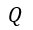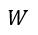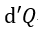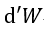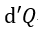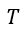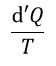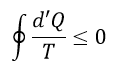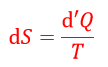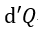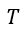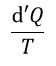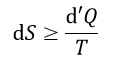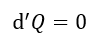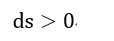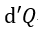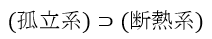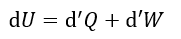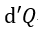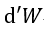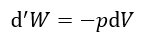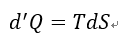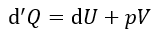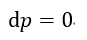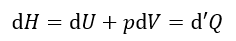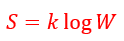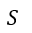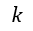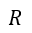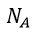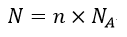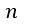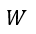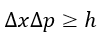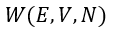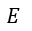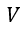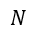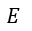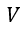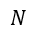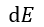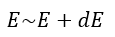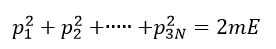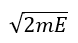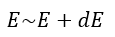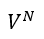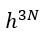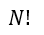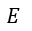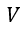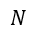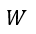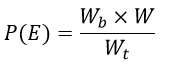エントロピーって？

よく、「エントロピー増大則」という言葉が使われています。

ネット調べて見ると、何か「自然の法則」なのだと当然のように言っている方々が多い気がします。
そして、色々な事象を、あたかも「エントロピー増大則」という言葉自体を何か「哲学的」な「自然
の摂理」みたいな位置づけで「自然で当然」みたいに適用されて大変失礼ながら、物知り顔で説
明して悦に入られているかのような感じがしてしまっています。中には、かっこよく「熱力学の第
二法則によると・・・」とおっしゃる方々もみられます。

で、私は、実際、「エントロピー」とは何かについて十分ご存知なのかなぁという大変失礼なことを
考えてしまっています。というのは、見ていると、多くの人は「エントロピー」というのは一体全体
何かということを述べずに「エントロピーは増大する」というフレーズだけを示されているからです。

恥ずかしながら、かく言う私はよくわかっていませんでした。エンタルピーってのもあったなぁ程度
で、一念発起して、熱力学から始めて基本から少し独習してみようという気になりました。エントロ
ピーに関して山のようにネットにある言説の信憑性を探るために・・・。天邪鬼かもしれませんが(^^;

熱力学の基本から独習しようと思い立ったのは、元々、「エントロピー」というのは熱力学で定義さ
れたものであるくらいは知っていましたが、熱力学自体は多分習ったとは思うのですが、そんなレ
ベルであり、ほとんど記憶の彼方所以でした。
で、そんなレベルなもので、仕事でも使うことが無かったゆえ、あったことだけは記憶の片隅にあ
るのですけど、手元には教科書なし（あるなら多分田舎の家）(^^;。

そこで、ネット上の解説サイトで学ぶことにしました。教材はEMANの熱力学。
ＥＭＡＮさんは、主に物理学に関して、よくあるような天下り式の小難しいだけの解説ではなく、実
にわかりやすく書かれていて重宝しているサイトです。勿論、「物理学」ですし、「言葉だけで説明
を試みている」啓蒙書の類とは違い数式が山のように出てきます。私は、数式は嫌いではなく、
むしろ理解するには必要なものであり、きちんと理解できなら納得できてしまう輩ですが、必ずひ
とつずつ自分で導出を確かめたりしようとする輩なので、沢山出てくると、どうしうても面倒になっ
てしまって、学習進行はその日の気分次第(^^;。頭が飽和状態になるとその日はやめて次の日へ
・・・ま、これは私にとっては気分一新になり、理解を進めていくのに丁度いいのです(＾◇＾)
というのは、数式を追うあまり、何のことの話なのか忘れてしまったりするからで、元に戻って熟
読するというようなことをしていて、斜め読みでは理解できんなということを悟ったからでした。
元々、浅学菲才の凡才ですが、頭はどんどん老化しているので。特に「記憶力」が(^^;・・・という
状況ですから。

で、最初に出て来たボイル・シャルルの法則（状態方程式と称するそうです）
・・・（1）
(圧力体積温度)
は知っていましたが、速攻で「全微分形式」が出てきました。状態方程式の全微分形式という説
明で。たとえば、(1)式から
であるので、全微分形式として
・・・（2）
ということです。

ま、別に「全微分」というのは知っていますので、特には驚いたりせず、何が始まるのかと私の興
味をそそりました。ただ、極めてお恥ずかしいことに、微分には「完全微分」と「不完全微分」
があり、上記の(2)のような形にできるのは「完全微分」だけで、不完全微分はそれができないも
のということを知りませんでした（忘れていただけかも？）。そして、それに合わせて、重要な概念
と思う「状態量」というtermを知り、状態量でないものは不完全微分であることを知りました。
「状態量」というのは、そこに至る経路が異なっていても同じ状態では同じ値を持つもの
だそうです。で、上記の状態方程式の中の圧力、体積、温度は「状態量」であり、(2)のようにそれ
ぞれ全微分形式で表すことができるというわけです。
しかしながら、熱量、仕事は状態量ではないそうです。
したがって、その微分形式は不完全微分となり(2)のような全微分形式では表せませんので、完
全微分と区別して、、のように表記することもあるようです。
なかなかエントロピーまで話が行かないのですが、これを述べておかないと話にもならないので。

さて、前述で、熱量は状態量ではないとして、その微小変化分は不完全微分だと述べました。
しかるに、
熱量の微小変化分を温度で除したを考えます。
理想的な熱サイクルとしての「カルノーサイクル」の研究結果から、
・・・（3）
という関係が求められています（クラウジウスの不等式と称せられている)不等号はサイクルの
途中に「不可逆過程」があるときです。
そこで、
・・・（4）
とおくことにします。そうしますと、(3)式左辺の周回積分というのは、このdsに沿ってぐるっと一周
積分することになるのですが、どこかを基準として例えばサイクル中のＡまでの積分値というのが
考えられます。これをＡ点におけるエントロピーと称しているようです。
エントロピーは状態量の一つであり、完全微分となります。
状態量ではない熱量の微分値を温度で除したをある区間足し合わせたも
のは状態量だというのですから不思議な気分になりますね。

もう少し詳細に説明しておきますと、サイクル中に「準静的過程でない」ところがあるとき、(3)式
の不等号が成立します。「準静的過程」というのは熱平衡が保たれている過程のことであり、「準
静的過程でない」というのは熱平衡が保たれていないということです。
原則的には、「準静的過程」ならば「可逆過程」(外界への影響も含めて完全に元に戻す過程）
であり、「可逆過程」ならば「準静的過程」であるので、前述のように「可逆過程」でない、すなわち
「不可逆過程」がサイクル中に含まれるなら(3)式の不等号になるということです。留意すべきは、
「準静的過程でない」途中ではエントロピーは定義できないということです。したがって、この過程
の前後ではエントロピーという状態量があるのですから、この区間の前後では、その値は不連続
となるということです。

したがって、(3)式より、考察過程は省略しますが、
・・・（5）
となります。サイクル中に「不可逆過程」があると、この式の不等号が成立するのです。
断熱条件のとき（熱の外部との出入りがないとき）はですので、(5)式は、
・・・（6）
となります。等号は、熱サイクルが「断熱で可逆過程のとき」であり、結局、
・・・（7）
というのは「エントロピーが増大する」ことを意味しますが、

　エントロピーが増大するのは断熱で不可逆過程があるとき

ということになります。
「断熱」でないなら、は正負の値を取りますから(6)(7)式とは限らないわけです。
したがって、少なくとも、最初に導入された熱力学におけるエントロピーの概念においては、「エン
トロピー増大」という（熱力学の第二法則になっていますが）のは理論的には条件付きであり、
「自然の要請でも自然の法則でも何でもない」ということになろうかと思います。

　「熱力学の第二法則は自然の法則である」と言う主張・
　説明は言い過ぎ

ではないでしょうか？

確かに、例えば、温めた水は加熱をやめれば冷めていき、突然、何もない状態でまた再び温まる
などということはないのは自然現象ですし、これは「不可逆過程」であることは間違いない事実で
しょう。これは「熱力学の第二法則」の普通の例ですね。

ただ、私が拘っていることは、「エントロピー」という「状態量」は温度、圧力、体積という測定出来
たり直観的にわかる状態量ではなく、理論研究過程で人為的に設定されたものであるとい
うことです。ですから、私は前述で「理論的には条件付き」と述べたのです。
尚、「孤立系」というtermがありますが、これは断熱系より厳しく、外部とは熱のやり取りがない(断
熱系)だけでなく仕事のやりとりもない系ということです。
ですので、断熱系での結論は孤立系でも成立するということです。

ちょっと考えると、熱量は状態量ではないのに、これを温度で除したものは状態量になり完全微分
で表すことができるって不思議じゃないですか？

余談になりますが、面白いことに、
・・・（8）
とおくと、このＵは状態量だというのです。ですから、dUという完全微分の形で表記しています。
そして、このＵのことを内部エネルギーと称しています。
外部との熱の出入りと仕事のやりとりの合計を内部に蓄積されたエネルギーと
みなすというものです。ちなみに、
・・・（9）
であり、エントロピーが設定できるところでは(4)式より
・・・（10）
となります。

更におまけですが、あと三つ「熱力学関数」とも称せられる「状態量」が定義されています。(8)(9)
式より
・・・（11）
となりますが、これから敷衍的に
・・・（12）
とするものをエンタルピーと称しているようです。あまり自然科学的なものではなく、
のとき、すなわち、圧力一定の時、
・・・(13)
となるよというだけでしかないようです。ま、逆にいうなら、圧力一定条件では、状態量でない熱量
が状態量であるエンタルピーになるとは言えます。計算式の簡単化のためにあるようなもので、
エントロピーや内部エネルギーよりずっと数学的で人為的な代物ですね。

他に、ヘルムホルツの自然エネルギー、ギブスの自然エネルギーと称するものがありま
すが、詳細は省略します。

ちょっと脇道にそれてしまいました。
いずれにしても、「熱力学の第二法則」の「エントロピー」というのは、ちまたで言われている「エント
ロピー」と随分、直接的な概念的にも、理論定義式も状況を異にしていることがわかると思います。
では、巷で云われている「エントロピー」とのつながりは一体全体何？ということになろうかと思い
ます。私といえば、そこに興味があったわけです。
そして、その答えは「統計力学」というものにありました。これについては、EMANの統計力学と
いうところを読みました。

「統計力学」というのは、気体分子論の研究から出て来たものなんですね。そして、ボルツマンと
言う方が、従来行われて来たものに対して革命的な考え方を示し、それが「統計力学」という学問
分野に昇華されたようです。
革命的と言いましたのは、どうやら、それまでは個々の粒子の運動を詳細に研究し論じることが
一般的であったのに対し、確率の考えを持ちこんで、、粒子全体での運動を考えて、いわば荒い
形で論じたものと言えるのではないかと。

いつの世でもそうですが、当然ながら当時の科学界からは猛烈な反発があったそうです。ただ、
ボルツマンに幸いし、科学の進歩と言う意味でも幸いだったことは、かのMaxwellが強力な支持者
になったそうだということです。あのMaxwellです。彼は既に、Maxwellの速度分布とかMaxwellの
速さ分布というのを提示してたようです。
Maxwellは熱力学にも足跡を残されています。やはりすごい人の一人だったわけで、４０代での早
死は惜しまれますねぇ。

で、統計力学におけるエントロピーはこのボルツマンのひらめき的思考によるもののようです。
・・・（14）
という金字塔なる数式を提示しました。彼のお墓にも刻まれているそうで、ボルツマンの関係式と
称せられているそうです。このＳは正確には「統計力学的エントロピー」と称せられているそう
です。実は、熱力学のエントロピーとの論理的関係がわからず色々とネット検索してみて了解した
のですが、

　この(16)式は熱力学から論理的に導出されたものではない

そうです。ですから、上記で「ボルツマンのひらめき的思考によるもの」と書いたわけです。
ネット上には「原理」とまで断定されている方がおられました。
尚、左辺のはエントロピー、はボルツマン定数です。
ボルツマン定数は熱力学でも出てくるもので、気体定数をアボガドロ数で除したも
のです。また、粒子数は
は(1)式のものでありモル数です。
ポイントになるのはです。微視的状態の数と称せられているそうです。
簡単に言えば、「Ｎ個の粒子群の運動パターンの数」というところでしょうか。

内部が真空の容器に仕切りを入れて二室とし、片方に気体を封入しておいて、この仕切りをはず
したとき、当然ながら片方に封じ込められていた気体は全体に広がりますから、後者は前者より
「運動パターン数」は増えることになり、これは、明らかに不可逆過程です。自然にそうなるのは、
「孤立系」でしょう。孤立系は断熱系を含みますので、このような自然的現象に熱力学の「エントロ
ピー増大」とのアナロジーを見出したものと思われます。

二つの容器のエントロピー全体は、それぞれのエントロピーの和で表されます。一方上記の微視
的状態の数の方はパターンの組み合わせとなりますから両者の乗算で表されます。そういう場
合、数学的に思いつくのは「対数」というわけです。

(14)式が対数関数になっているのは、そういう思考過程からのものです。
直接、熱力学から導出された数式ではないことは明らかですね。全くの別発想ということです。
但し、そこがボルツマンのすごいところだと思うのですが、ボルツマン定数が対数に掛けられてい
ることです。詳細は省略しますが、これで熱力学において導出される関係式が出てきて、熱力学
と繋がるようになっています。要するに、全くの別発想から(14)式を作り出していますが、結果論
として熱力学との辻褄合わせができているということです。

しかし、この(14)式、まだ、よく出てくる式と異なりますよね。ただ、(14)式を眺めているだけでは何
も次に進まないということです。基本的に、Ｗを求めないとエントロピーＳが求められないからです。
で、次の課題は、「微視的状態の数」ってどうやって求めるのかということです。
私のような凡人には全く思いもつかないような考察がなされています。１個の粒子のある瞬間の
状態は三次元座標と三次元運動量の６個の次元で決まりますが、Ｎ個の粒子をまとめた６Ｎ次元
位相空間であるガンマ空間というのを想定し、このガンマ空間上の1点（代表点と称します）はＮ
個分の全粒子のある瞬間における状態を示すことになり、先の「運動パターン」はこのガンマ空
間の代表点の運動パターンということになりますが、問題は、そんなものは無限にあって数える
ことなどできないではないかと言う話です。

巧妙なことを考えているのですね。古典的な「連続」という考え方を捨てて量子力学知識を入れ
て考えるのです。位置座標と運動量の積は「角運動量」となります。量子力学の「不確定性原理」
の左辺は「角運動量」の次元で、これの最小はプランク定数だということになります。（プランク定
数は角運動量の次元を持ちます）。すなわち、これより微小な領域は区別がつかないということ
ですから、これを最小単位にして数えるのです。
要するに、６Ｎ次元ガンマ空間に置いて代表点が取りうる領域というのは、３Ｎ次元位置座標に
よるＮ個分の球の組み合わせと3Ｎ次元運動量空間における球との組み合わせすなわち両者の
積＝角運動量を最小の運動量次元を有するプランク定数の3Ｎ次元での組み合わせの運動量で
除すことで微視的状態の数Ｗが有限個の数として求められるという事です。

このことを念頭に置いて、ＥＭＡＮさんの統計力学には５つの場合の算出方法が示されています。
最初は数式に惑わされてしまって、何をしているのかという流れがわからずなかなか理解できな
かったのですが、繰り返し読んでなんとかおぼろげながらわかった気がしています。

いずれにしろ、「微視的状態の数」Ｗをとして、(エネルギー)(体積)
(粒子数)の関数とします。
その基本的なのは４つですが、「小正準集団（ミクロ・カノニカル・アンサンブル）」「正準集団（カ
ノニカル・アンサンブル）」「大正準集団（グランド・カノニカル・アンサンブル）」というものと、「定圧
集団」というものです。色々と近似的考察が入っていて、微小という事で邪魔な項がneglectされた
りしています。

最も簡単なケースは、１個孤立系の場合で、、を一定とするものです。
これの解析を「小正準集団」の手法と称しているようです。
エネルギー一定ということは、ガンマ空間においては、等エネルギー面と称せられる面上に代表
点は拘束されてしまうのですが、これは面であり、このままでは体積が出てきません。
そこで、実際にはエネルギーには揺らぎがあるとして、等エネルギー面を
のエネルギー範囲部分とするのです。う〜ん、巧妙ですなぁ。
ちなみに、前述の3Ｎ次元運動量空間の球ですが、エネルギーを運動エネルギーとすると、
となり、これは半径がの3Ｎ次元運動量空間の球の式となります。
したがって、この球でエネルギーがの部分の体積に、３次元空間座標系の球
の組み合わせを乗じたものをで除せば求まるはずですが量子力学の示すところ
によればそれでは同じ状態を重複して数えていることになるので、前述の結果をで更に
除してやる必要があります。これ以上の算定は数学の高度の公式が使われており本稿の議題
の本質ではないので省略します。

議題の本質に近づくためには、小正準集団のような１個の孤立系ではなく、対象の粒子が入って
いる容器系が更ずっと大きい(体積、粒子数)容器(熱浴系)の中にあるような場合、対象の容器内
の粒子がある状態になるときどうなるかを考える必要があります。

極めて巧妙で、ずっと大きな熱浴系に対象の容器系が接している形のモデルに置き換え、両者
全体は孤立系、そして二つをそっと離せばほとんど影響はないとしてそれぞれも孤立系だとみ
なしています。全体は孤立系ですから、全体のエネルギー、粒子数は一定です。
そういう中で、容器系が、、、という状態になるときを確率の考えを入れて解析
しています。微視的粒子数を
全体：、熱媒系：、対象容器系
としますと、この確率というのは
　　(15)
で与えられと考えられます。

以下、共通して温度一定で、エネルギーは両容器で交換する（容器系のエネルギーは一定では
ない）４つのケースを簡単に示します。
(1)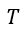,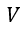,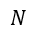一定で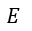のみ熱浴系との間で出入りして変化する場合
正準集団の手法を用います。結果のみ示します。
規定化関数を
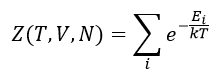　　(16)
とおくと、出現確率は
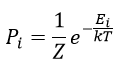　　(17)
そして熱力学の内部エネルギーはこのエネルギーの平均値となり、
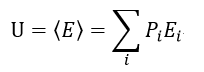　　(18)
となります。エントロピーは
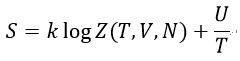　　(19)
となります。
パラメータが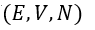⇒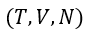となっています。

(2)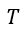,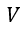一定で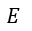のみならず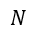も熱浴系との間で出入りして変化する場合
正準集団の手法を用います。結果のみ示します。
規定化関数を
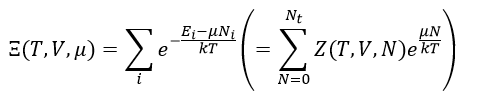　　(20)
とおくと、出現確率は
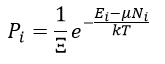　　(21)
また、
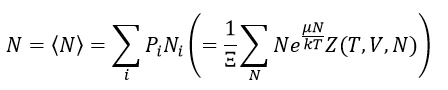　　(22)
となるので、エントロピーは
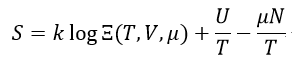　　(23)
となります。ここで、μは化学ポテンシャルです。
パラメータが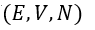⇒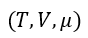となっています。

(3)、、を一定とし、のみならずも変化する場合
規定化関数を
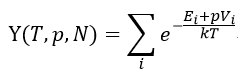　　(24)
としますと、出現確率は
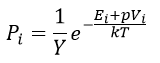　　(25)
また、
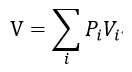　　(26)
となるので、エントロピーは
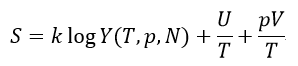　　(27)
となります。
パラメータが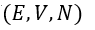⇒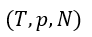となっています。

(4)、、を一定とし、のみならずも変化する場合
規定化関数を
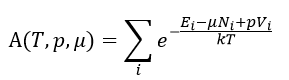　　(28)
としますと、出現確率は
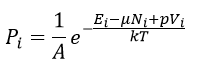　　(29)
となるので、エントロピーは
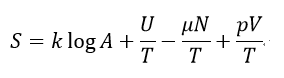　　(30)
となる。
パラメータが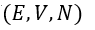⇒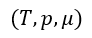となっています。

以上の式を見ると、次の形になっています。
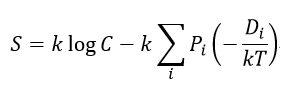　　(31)
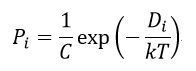　　(32)
(32)より、
となるので、(31)に代入すると
となります。もう一度書きますと
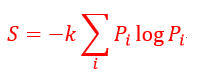　　(33)
というよく見る式が導出されたわけです。
ちょっと誤解していましたが、エネルギーも一定として論じた小正準集団はどうなの？と思ったの
ですが、この(33)式はそれも含むことがわかりました（説明は省略）。

ＥＭＡＮさんによれば、教科書によっては最初からこの(33)式を出しているものもあるそうです。
それで、わかりました。巷で言われている話は、「エントロピー増大則」とこの式から敷衍したも
のだと。

しかしながら、この式は、あくまで、前述のような考察から、数学的に導かれたものでしかありま
せん。何もないところから突然ぽっと出てきたものでも何でもないわけです。
この式に至るまでの理論過程においては、かなり近似的考察を重ねています。邪魔な部分を値
が小さいとからとしてneglectもしています。証明できないからと「原理」と言う名称を使う「等重率
の原理」という概念も入っています。そして、私が気になっているのは「孤立系」という仮定の元に
論じられていることです。
したがって、いくら「美しい式」が導出されようと、「美しいから」といって、「自然の要請」というのは
単なる思い込みではないかと思うのです。「自然」がそれらのいわば人間がなした「仮定」通りか
どうかなど証明されていないからです。

繰り返しますが、そもそも、エントロピーというのは熱力学で定義されたものですが、あくまで、人
為的に定義された概念です。全ての人が自然に思念できるようなものではありません。
しかも前述のように、「エントロピー増大」は熱力学の理論的な結論ですが、そこでは「断熱系」と
いう条件が厳然と入っているのです。全ての場合に成り立つものではないのです。
(33)式は断熱系より厳しく断熱系を包含する「孤立系」という場合で理論展開した結果です。そし
てその式の元になった(16)式は前述のように熱力学から論理的に導出されたものではないという
ことです。その意味で、区別して「統計力学的エントロピー」と称しているということは前述しました。
近年、情報理論の方面で、1と0というビット単位関連が丁度、ボルツマンの(16)式と類似している
ということから、「情報エントロピー」という概念が生まれています。ｋの値は異なりますが。

結局のところ、「エントロピー増大」というのは、元々の定義である熱力学については、「熱力学
の第二法則」という「言葉」だけが使われ、後は、(33)式、そして、補填的に情報エントロピーか
ら「思いついた」ものを、いかにも「自然の法則」であるかのように論じているというのが事実で
はないでしょうか？

以上より、例えば「時間の矢は熱力学の第二法則より説明できる」というのは、論理的でない思
い込みから来るフレーズであると考えます。
また、ごみが散らかることをもって、エントロピー増大を説明するのは、本末転倒かつ真の証明
にもなっていない議論だと思います。

要するに「エントロピー増大」というのは、摩訶不思議な自然の法則でもなんでもなく、単なる一
つの科学理論以上のなにものではないと私は思うのです。

元々は、熱力学第二法則に関するある議論対立を目にして真相を知りたいと思って調べたので
すが、私自身浅学菲才の身、付け刃的な今回調べた知識の中ではその答えは見つかりません
でした。もっとも、私は上記の自分自身の結論からその議論自体おかしな話だと思っていますか
らどちらがどうのというのではなく、そこに持ち出されていた「科学的」な部分への興味です。
もう少し調べて見る必要があります。

　('16/7)

目次に戻る