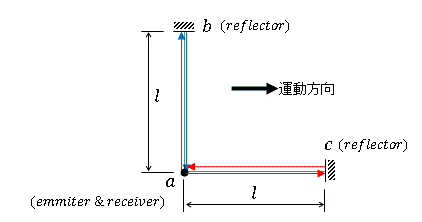
 |
| 図1 |
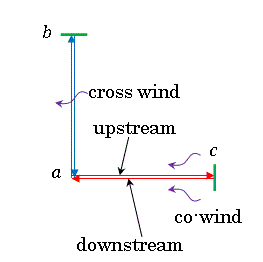 |
| 図2 |
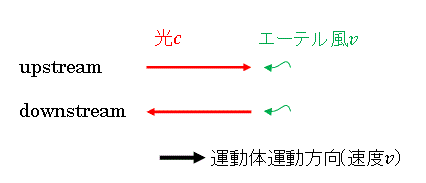 |
| 図3 運動体上でのエーテル風と光の進行 |
| emmitor〜reflector間距離を | 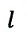 | 、光速を | 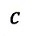 | 、運動体速度を | 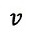 | としますと、 |
 | ・・・(1) |
| upstream速度: | 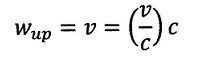 | ・・・(2) |
| downstream速度: | 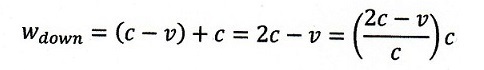 | ・・・(3) |
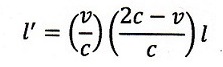 | ・・・(4) |
| upstream: | 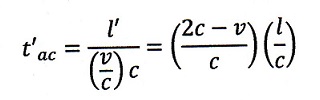 | ・・・(5) |
| downstream: | 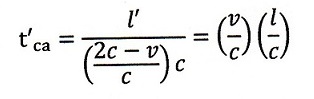 | ・・・(6) |
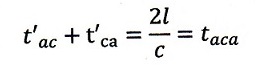 | ・・・(7) |
 |
| 図4 |
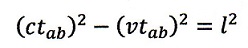
|
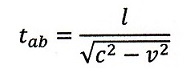 | ・・・(8) |
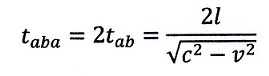 | ・・・(9) |
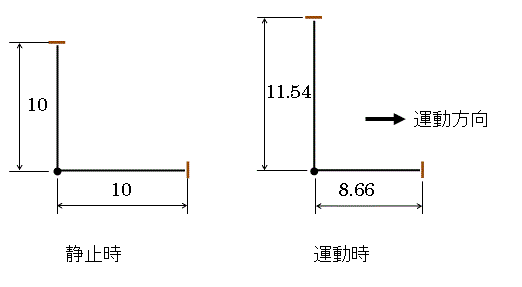 |
| 図5 Lorentz's "initial mistake"?(数値例) |
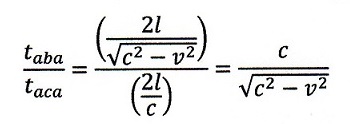 | ・・・(10) |
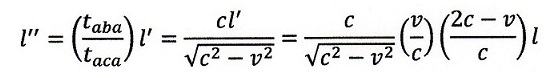 | ・・・(11) |
| upstream: | 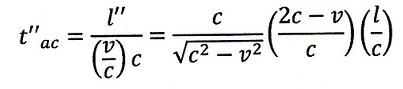 | ・・・(12) |
| downstream: | 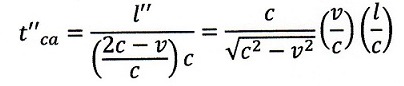 | ・・・(13) |
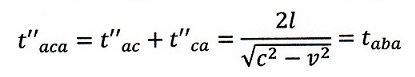 | ・・・(14) |
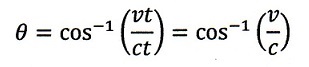 | ・・・(15) |
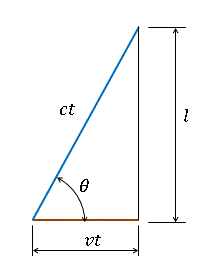 |
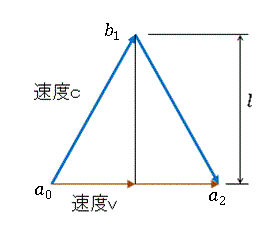
| 図6 crosswind光路の半分が作る三角形 |
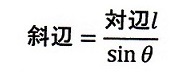 | ・・・(16) |
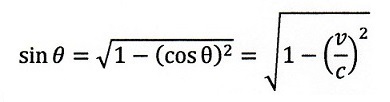 | ・・・(17) |
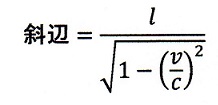 | ・・・(19) |
| したがって、crosswindの全光路長 | 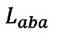 | は(斜辺)×2ですので、 |
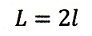 | ・・・(20) |
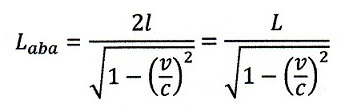 | ・・・(21) |
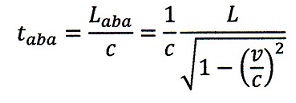 | ・・・(22) |
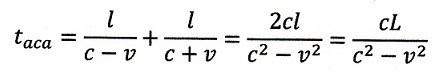 | ・・・(23) |
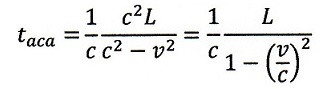 | ・・・(24) |
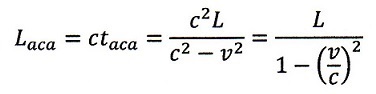 | ・・・(25) |
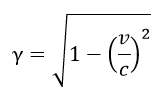 | ・・・(26) |
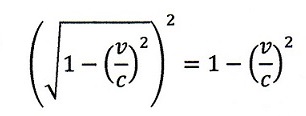
|
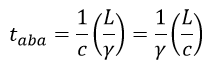 | ・・・(27) |
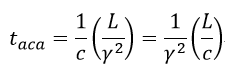 | ・・・(28) |
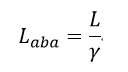 | ・・・(29) |
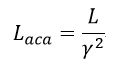 | ・・・(30) |
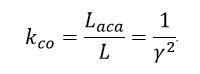 | ・・・(31) |
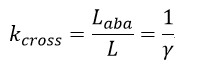 | ・・・(32) |
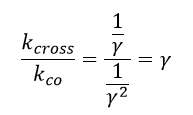 | ・・・(33) |
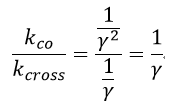 | ・・・(34) |
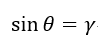 | ・・・(35) |
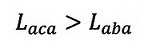
|
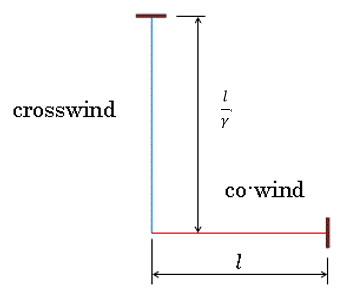
| 運動体の速度は光速に対し、 | 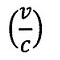 | ですので、光がco-wind光路(co-wind腕長さが |
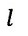 | のままのとき)を往復する間、運動体は | 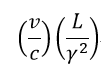 | だけ動くことになります。 |
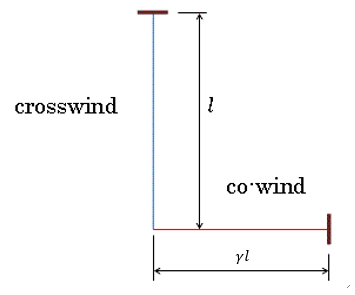
| これは図4で茶色で表した底辺になり、図6の半分の三角形の底辺長さは | 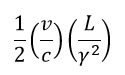
|
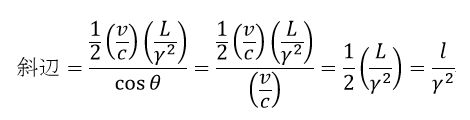 | ・・・(36) |
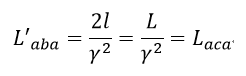 | ・・・(37) |
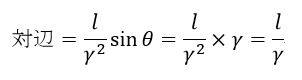 | ・・・(38) |
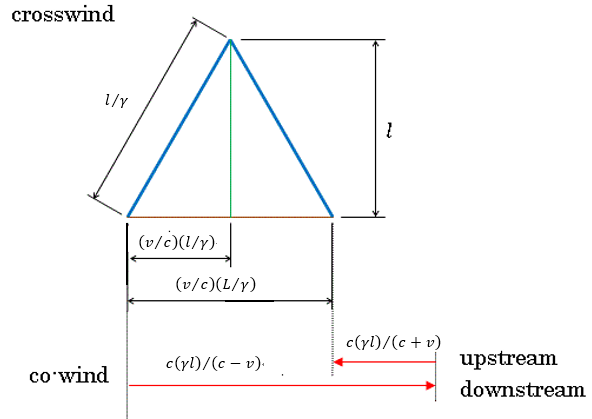
| 結局、co-windの腕の長さを | 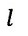 | のままとしますと、同時到着のためにはcrosswindの |
| 腕の長さが | 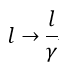 | と | 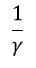 | だけ伸長されている必要があります。 |
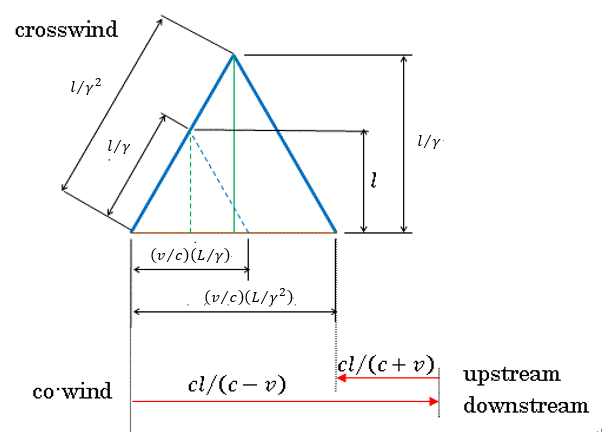 |
| 図7 伸長されたcrosswindの腕/光路及び変化させないco-wind光路 |
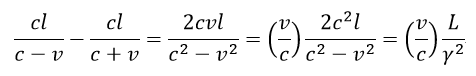
|
 |
| 図8 crosswindを伸長して時間合わせしたときの腕長さ |
| crosswind腕長さを | 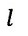 | のままとすると、斜辺長さは | 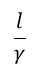 | となります。 |
| るまでの運動体の運動距離は | 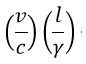 | となります。したがって、crosswindの光が |
| receiverに戻ってくるまでの運動体の全運動距離は | 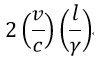 | となります。 |
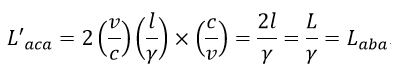 | ・・・(39) |
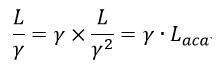 | ・・・(40) |
 |
| 図9 伸長されたcrosswindの腕/光路及び変化させないco-wind光路 |
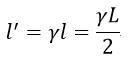 | ・・・(41) |
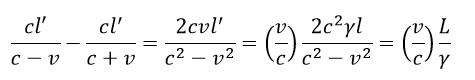 |
 |
| 図10 co-windを短縮して時間合わせしたときの腕長さ |