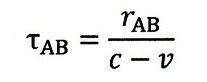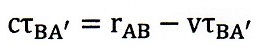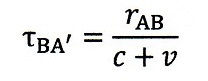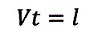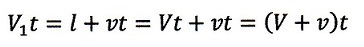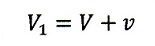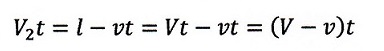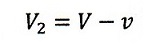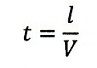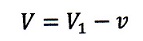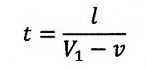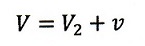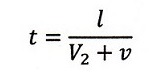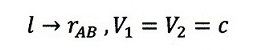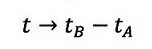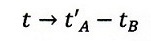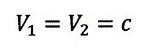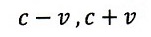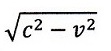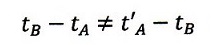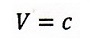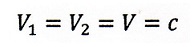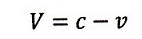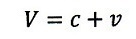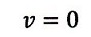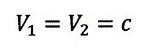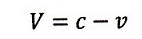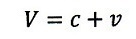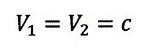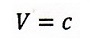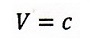「特殊相対性理論」への疑念(全面改定版4)
〜原論文での理論の疑問点②〜
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
・・・・・・・・・・・・・・・・・・・・・
※疑問を抱いてから思考の紆余曲折を経て(17)まで書いてしまいましたが、重複・誤解・
後から得た知見などもあるため、本タイトル分は整理しての全面改定で再編成しました
('14/4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
・・・・・・・・・・・・・・・・・・・・・
さて、①(ここ)につづき、もう少し原論文”ON THE ELECTRODYNAMICS OF MOVING
BODIES”についての考察を続けます。
尚、読むに当り、特に、原論文に詳細に言及している下記サイトを参考にさせていただ
きましたm(__)m。
・参照サイト①
・参照サイト②
参照サイト②の方の御主張が頭にあり、論文を読んでいて大変気になったことがありま
す。
論文中にtimeという用語が出てきます。原論文はドイツ語だそうで原論文はどうなのか
わかりません(調べたらドイツ語も同様だそうです)が、英語でtimeというのは日本語で
は「時間」及び「時刻」の両方の意味となります。日本語の「時刻」というのは7時とか
12時とかいう時計の針が示している「時」を示す「値」ですが、本来、「時間」というのは
「時と時の間」を示す概念のはずです。しかし、考えてみると、理系は「時間tにevent1が
おきる」という風に、本来は「時刻」であるところに「時間」という用語を平気で用いていま
す(私自身も特別に考えもせずそういう使い方をしてきました(^_^;))。明らかに、西欧科
学を取り入れるとき、この"time"という語彙がそういう風に使われたことによるでしょう。
しかし、このEinsteinの論文で出てくる、timet(静止系のtime)、τ(運動系のtime)は同
じ変数名のままで「時刻」と「時間」の両方で使われていて区別がされていません。ただ、
不思議なのは、論文の§2の中で明確に、
 | ・・・(1)
|
と書いており、速度と距離の式に出てくるのは厳密の意味での日本語の「時間」という
ことですよね。"time interval"と書いているのですから。
ま、話はそれますけど、大変興味深いことに、この式、右辺分子が"light pass"と書かれ
ているのに、左辺は、ただ"velocity"とだけあることです。「どういう速度(velocity)なのか」
の説明はありません。ちなみに、この式を変形すれば、
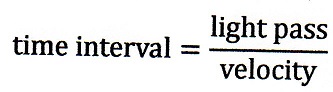 | ・・・(2)
|
ですね。しかしながら、論の過程の中で、
最初は、「時刻」の意味で使っているtimeが、同じ変数のまま、途中
から「時間」の意味に転用されて使われて解析が進められている
のです。
§1項で最初に出てくる「時計合わせ」の式である
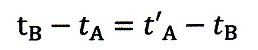 | ・・・(3)
|
の
は間違いなく「時刻」の意味合いですし、このとき、「時間」はこの両辺の差分式ですよね。
すなわち、これが"time interval"ですね。
また、§3の中に出てくる「timeτ0で光が発射され、timeτ1で反射され、timeτ2で元の
位置に戻る」という説明の
はこの説明の時点では明らかに日本語の厳密な意味での『時刻』のはずであり、この中
で出てくる
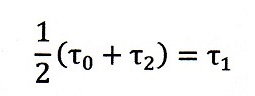 | ・・・(4)
|
という式は、論文では明示されてはいませんけど、明らかに
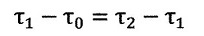 | ・・・(5)
|
というもの(postulate①であるEinstein's"Principle of Relativity"に基づいてそうなるとし
たのでしょう)から出てきた式で、この両辺の差分式が「時間」になります。
しかしながら、彼は、(4)式の各変数を4つのパラメータを持つ関数として、
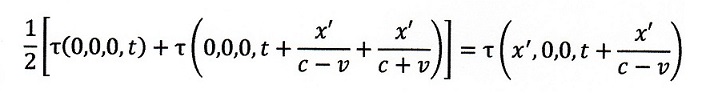 |
|
・・・(6)
|
という式を出してきています。このうち、前の3個のパラメータは「座標」値らしいのです
が、第一パラメータは
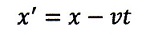 | ・・・(7)
|
となっています。但し、わかりにくいのですが、これを、運動座標系の任意の静止点、
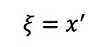 | ・・・(8)
|
として、運動座標系[彼はその座標軸を(Ξ、Η、Ζ)、各座標値を(ξ、η、ζ)で表して
います。ちなみに、ξは「グザイ」と呼びΞはその大文字、ηは「イータ」と呼びΗはその
大文字、ζは「ツェータ」又は「ゼータ」と呼びΖはその大文字]内の座標として時間tに
無関係に選んだものとしています。
第二、第三パラメータはη=y、ζ=z[Η、Ζ軸はそれぞれ静止座標系の座標軸(X,Y,
Z)のY,Z軸に平行としています]というものですので、前3個は運動座標系上の任意の
1点の運動座標系座標と言えますね。
ただし、第4パラメータは「運動系の『時刻』」
に対応する「静止系の『時刻』となっていますので、『運動系の空間座標』と『静止系での
時刻』がパラメータになっているちょっと煩雑なものになっています。
問題はその次です。彼は、この(6)式から、説明なしで、x'を無限に小と「仮定」して偏微
分の式
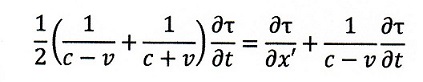 | ・・・(9)
|
を導出しています。これは(6)式を二つの独立パラメータt,x'の関数とみなして、独立二
変数に関するTayler展開して、一次成分だけとると出てきます。しかし、あくまで、
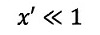 | ・・・(10)
|
でしか近似的に成立しません。そして、(10)となる根拠は不明です。しかも最後まで説
明なしです。
ま、その点は置いておいて、ここで私が気にしているのは、参照サイト②の方が指摘さ
れているように、この時点でパラメータにおいて、
運動系の『座標値』が『距離』
τとかtが『時刻』から『時間』
の意味に転化していることです。
正直、私もこれまで気にもしていませんでしたが、参照サイト②を目にしてはたと気がつ
いたのですが、『微分』というものの定義を考えてみれば、その対象は、『距離』、『時間
("time"を「時刻」の意味で用いるなら"time interval")』であらねばなりません。
ま、こういうと、それまで気にもしていなかったのに、頭のよい人はすぐ考えて、
「いや、
座標軸原点からの軸方向距離=その軸での座標値
基準時刻を0とした経過時間=そのときの時刻
であるから問題ないだろう」と反論すると思います。しかしながら、その時点でもう、彼は
「どつぼ」に嵌っているのに気がついていません。そう考えた時、何が問題かは前述の
サイト②で詳述されていて、私は「なるほど」と思いました。「相対性理論」が言うところの
「光時計」をころっと忘れてしまっているのです。矛盾が出てきます。
そして、この
「時刻」と「時間」、「座標値」と「距離」の混同
は色々な場面で後世の学者の本にも出てくるようです。「時刻」にローレンツ変換を掛け
てみたり・・・。
さて、もう一つは深刻です。
§2の終わりの方で、何の説明もなく突然、下式が示されています。
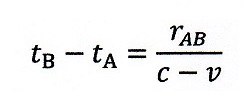 | ・・・(11)
|
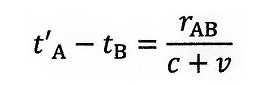 | ・・・(12)
|
これは、運動系の中に固定された剛体棒の両端A,Bに時計(静止時に静止系の時計と
時計合わせされている)を置き、運動系が速度vで運動している時、運動方向にA点から
B点に光を発射し、B点で反射させてAに戻ってくるという「時計合わせ」方法を運動系内
で適用したとき、その発射(A位置)、反射(B位置)、戻り(A位置)のそれぞれの時点の
静止系位置における時計で見るとこうなり、運動系の中では(5)式とならないという説明
のところで出て来ているのですが・・・。
Einsteinはどのように考えたのでしょうか?
実はこの式は、マイケルソン=モーリー実験に関するローレンツの理論に出てくる式そ
のものです。どうやら、当時はその考え方が学界では受け入れられていた学識だったら
しいという情報も目にしています。
ちなみに、まちがいなく、Einsteinも往路を(11)式、復路を(12)式としています。(9)式に
もそれが明確に現れています(後世の人達の説明では逆になっているのもあるらしいで
すがなぜなのでしょうか?元の考え方を誤解しているのではないかと思います)。
これらの式の導出としてよくある説明は以下でしょう。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
まずは式を簡単にするため、
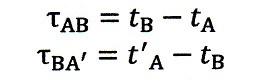 | ・・・(13)
|
とおきます。
A⇒Bの光路に対しては、B端が速度vで発射地点から遠ざかって行くため、静止系から
見ると、光路長がv・τAB分長くなり、
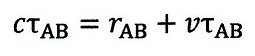 ・・・(14) ・・・(14)
|
となるので、変形すれば、
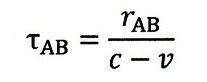 | ・・・(15)
|
となります。
一方、B⇒Aの光路に対しては、A端が速度vで反射点Bに近づいてくるため、光路長が
v・τBA’分短くなり、
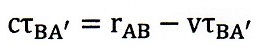 | ・・・(16)
|
となるので、変形すれば、
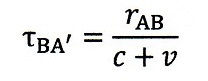 | ・・・(17)
|
となります。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
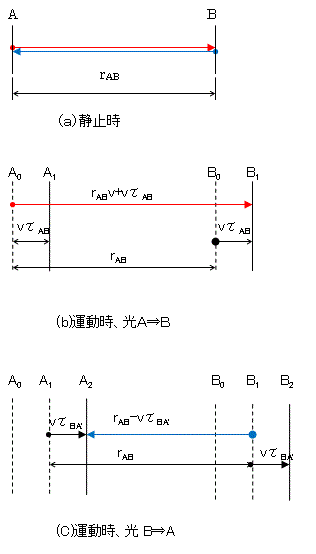
これをわかりやすく図に示すと下図となります。
 |
|
図1
|
A0、B0はtimetAに光が発射されたときのA点及びB点の位置、A1、B1はtimetBに光が
B点で反射された時のA点及びB点の位置、A2、B2はtimet’Aに光がA点に戻ってきた
ときのA点及びB点の位置です。
いずれにしろ、(15)式は(11)式と、(17)式は(12)式と完全に一致しています。
実は、私は誤解していて当たり前のように図1から上のようにして(15)、(17)式を出して
いたのは、すでに相対性理論の予備知識が頭にあったためと思います。しかしながら、
ローレンツ達は相対性理論が出る前の19世紀に上のようにして考えたのです。
よくよく考えると、上記の往復時間の導出の考え方の基本は、
光速cは「静止エーテル系」に対して一定である (※)
という「当時の」学界の思考に従ったものであると考えられます。(※)が「正しい」とする
なら、図1と上記の(13)〜(17)式の計算の流れは数学的に合理的です。
しかしながら、Einsteinは
静止エーテルは考えなくてよい(エーテル否定;"no ehter"ideals) (※※)
として相対性理論を導きました。では、彼は「何の説明も無く突然出した」この当時の学
識らしき式(10)、(11)をどう理解したのでしょうか?そして、後世の人々はどう理解し
ているのでしょうか?
もう一つの解釈として、
運動系を静止系から見た時、相対的にこうなる (※※※)
というのがあります。
これについては、従来からの物理知識として、速度に関する『ガリレイの相対性原理』
があり、それを流用した考え方となります。私も誤解していたのですが、マイケルソン=
モーリー実験のローレンツの理論をひょっとしたらこちらで解釈されているのではないか
と思います。そして、Einsteinはこちらで考えたのではないかと思います(事実は不明で
すが、私は情況証拠的にそう判断しました)。
これは、「静止系に対して速度vで運動している系内において、速度Vで動いている物体
の運動を静止系から見たらどうなのか?」というもので、具体的には、相対運動に対して
『ガリレイ変換』が使用されています。
そこで、これで考えることにします。
ます、これは、
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
運動系内での移動距離をl、移動速度をV、その時間をtとしたとき、
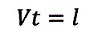 | ・・・(18)
|
であるので、以下となる。
・vとVが同じ方向のとき:
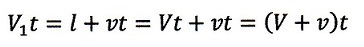 | ・・・(19)
|
より相対速度は
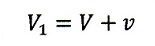 | ・・・(20)
|
・vとVが反対方向のとき:
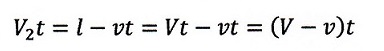 | ・・・(21)
|
より相対速度は
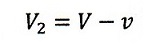 | ・・・(22)
|
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
というものです。
(18)式より、
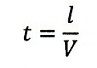 | ・・・(23)
|
となります。
・vとVが同じ方向のとき:
(20)式より、
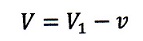 | ・・・(24)
|
であるので、(23)、(24)式より
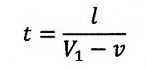 | ・・・(25)
|
・vとVが反対方向のとき:
(22)式より、
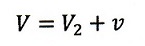 | ・・・(26)
|
であるので、(23)、(26)式より
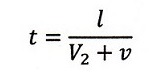 | ・・・(27)
|
となります。そこで、(25)、(27)式で、
とおいて、(25)式で、
(27)式で、
とおけば、それぞれ(11)、(12)式と一致します。
この、
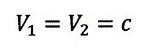 | ・・・(28)
|
は、
静止系から見た運動系の中の光の光速もcである (※※※※)
ということに相当します。この考え方を前述の(※※※)で表現したのです。
しかしながら、これらの(11)、(12)式をよく見てください。これらの式を(2)式と比較すると、
となりますね。ローレンツ達は、Einsteinが相対性理論を発表する前、この
という"velocity"を何だと考えたのでしょうか?
具体的言及をしていませんが、あえて考えるなら、ローレンツら19世紀の考えは、
それぞれ、地球系(運動系)の観測装置の公転方向光路の
往路、復路における光の相対速度
というものではなかったかと思われます。幸い、マイケルソン=モーリー実験はこんな往
路、復路、更には往路+復路の時間を測定した実験ではありませんでしたし、当時は地
球上での精密な光速測定はなされていなかった(別項で触れますけど、現在c値として
使われている高精度な数値の測定結果が最初に認められたのは1958年です)ため、当
時はこの発想が破綻しなかったわけです。
また、Einsteinは何だと考えたのでしょうか?論文内で(1)式を提示している(ですから、
当然(2)式が出てきますが)のに、これまた、言及はなく、後世の学者も言及していませ
ん。ただ、Einsteinは直角方向については、(※)の原則の下で作られたローレンツ達の
式での、
をこれまた、何の説明もなしに、突然提示している上に、「相対速度」などと書いてます
ので、名目的には「相対速度」としたのだろうと思いますが、相対性理論の概念からする
とずいぶんいい加減で「ご都合主義的」思考という気がしています。相対性理論の概念
で考えるなら、単に「数学的に出てくる」だけのものというしか言えない気がします。
どうやら、現在の学者は「座標速度」などという勝手な名称を付けているそうです。
でも、なんですか、これ?全く物理的意義のない用語ですなぁ。
Einsteinもこの(11)、(12)式の意義まで考察せず、その計算式だけに着目し、自分
が作った(3)式の「時計合わせ」定義から考えて、
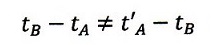 | ・・・(29)
|
となる、これは「それまでの物理常識が間違っていたことを示している」と思ってしまった
んですね。そして、彼は一歩進んで、
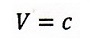 | ・・・(30)
|
とし、結局、
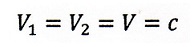 | ・・・(31)
|
としたわけです。
しかしながら、これはよ〜く考えてみれば、実に「おかしな」ことをやっていることに気が
つくはずなのですが・・・。
前述のように、原論文の中でEinsteinは説明なしで(10)、(11)式を提示していて、これは、
当時の学界の学識と一致した式であった一方で、前述のようにガリレイ変換で、相対速
度を(28)のようにおけば同じ式が導出されるため、意図的かどうかわかりませんが、図
もないことも幸いして「あれっ?おかしくない?」と現在まで科学者達が気がつかないま
まになってきたのではないかと思います。
再度、前述の『ガリレイ変換』の行程を考えてみましょう。
(24)、(26)式に着目してください。
・vとVが同じ方向のとき:
(24)、(28)より、
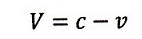 | ・・・(32)
|
・vとVが反対方向のとき:
(26)、(28)より、
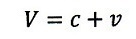 | ・・・(33)
|
となります。
しかしながら、ここで、(30)式が成立するとすると、いずれも、
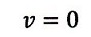 | ・・・(34)
|
となってしまいます。したがって、(11)、(12)式を「ガリレイ変換」から(28)式として求める
とき、更に(30)式とできるのは、(34)のとき、すなわち、
運動系が静止系に対して静止している時のみ
なのです。この事実を無視して、(11)、(12)式だけ採用するというのは道理にあいませ
ん。そんな不合理をよしとするなら、それはもう全く「科学的・論理的」態度ではありませ
ん。Cultでしかないのです。なぜなら、(31)式など金輪際、実証証明されていないから
です。
結局、Einsteinが(11)、(12)式をそのまま使用した時、考察が杜撰だったのです。
そして、多くの人がしっかり考えていない気がします。
なぜ、皆が「おかしい」ということに気がつかないのか・・・。それは、(11)、(12)式の形に
あるのです。これらの式では"velocity"として、cとvだけが入っています。vは地球系(
運動系)の速度とわかっていますが、cは「光速」といいながら、「どこにおける光速なの
か」明確化されていないのです。いや、ローレンツら19世紀の頃は、きちんとしていて、
前述のように(※)です。しかし、「静止エーテル不要」の相対性理論ではそれが曖昧な
のです。
しかしながら、Einsteinの論文に従えば、「静止エーテル不要」とするなら、上記の導入と
なるのです。先に光速のところに別の変数を入れて置いてやればわかるのですが、上
記の考え方と比較してみれば、(10)、(11)式には(32)式または(33)式の"V"すなわち、
地球系(運動系)内の光速を直接表す変数は入っていないのです。
だからこそ、前述の矛盾に気がつかないのです。
19世紀の終わりから20世紀の初めに戻って整理してみましょう。
マイケルソン=モーリーの実験に対して、実験装置における公転方向(東西方向)の光
路に関して、
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
●ローレンツの場合:(※)光速は静止エーテル系に対して一定
|
・静止エーテル系光速: |
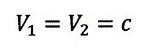 |
|
・地球系光速: |
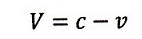 | :往路時 |
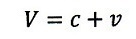 | :復路時
|
●Einsteinの場合:全ての慣性系で光速一定
|
・静止エーテル系光速: |
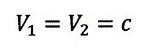 |
|
・地球系光速: |
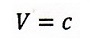
|
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
ということです。
前述のように、すでに、地球系光速に対しては
が実測されています。したがって、ローレンツら19世紀の(※)の発想は「誤り」ということ
です。一方、Einsteinの発想の方は前述の矛盾((34)式でしか成立しない)が出てしまう
のです(Einsteinは論文内で(11)、(12)式を提示し使用していますから、間違いなく先に
(28)式を考えていたはずです)。
結局のところ、(11)、(12)式からスタートしたこと自体、共に誤っているのですが、当時
は精密なcの測定がまだなされていなかったため、だれも気がつかなかったのです。
しかも、金輪際、(11)、(12)は実測証明されておりません。
後世の皆さんは、(11)、(12)式がローレンツら19世紀の学者の式と同じだったことから、
図1だけで考え、そしてそれらの時間の式にはcとvしか入っていないために落とし穴に
嵌っていてそれに気がついていないのです。
結局、
Einsteinが考えた「時計の狂い」はただ単に"Einstein's World"だけ
にあるおとぎ話
に過ぎないのです。"True World"のものではありません!!
私的には以上で「はい、終わり」のつもりだったんですが、とても気になる情報を目にし
てしまいました。全く持って奥が深すぎます。これについては別項で。
(’14/4) (続く)
目次に戻る
次へ


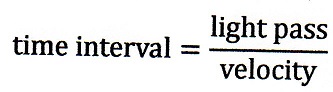
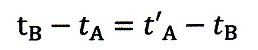
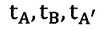
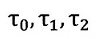
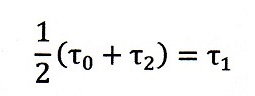
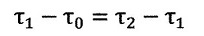
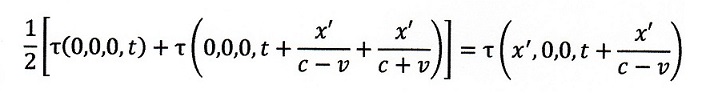
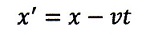
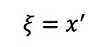
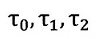
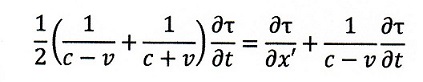
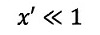
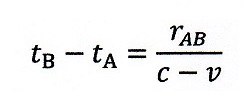
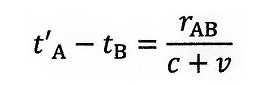
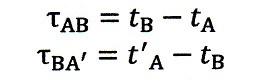
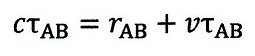 ・・・(14)
・・・(14)