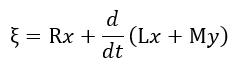
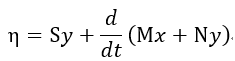
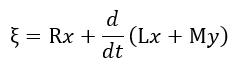 | (1) (一次側回路に対する) |
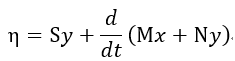 | (2) (二次側回路に対する) |
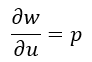 | (3) |
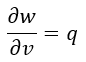 | (4) |
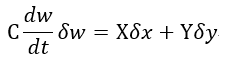 | (5) |
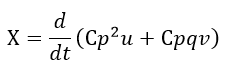 | (6) (for A) |
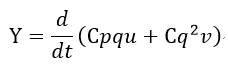 | (7) (for B) |
| 「運動量は質量×速度」であることを勘案すれば、 | 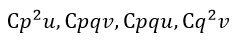 | は |
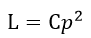 | (8) |
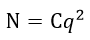 | (9) |
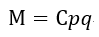 | (10) |
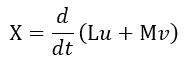 | (11) (for A) |
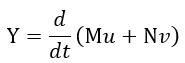 | (12) (for B) |
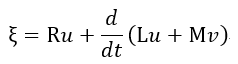 | (13) (for A) |
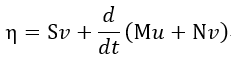 | (14) (for B) |
| また、上記の「機械の動力学」とのアナロジーから、 | 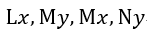 | を「電磁運動量 |
| 尚、(1)(2)式における | 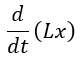 | 、 | 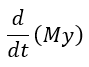 | 、 | 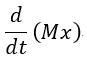 | 、 | 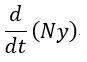 | は現在、 |
| 「逆起電力」と称され、 | 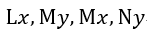 | は「鎖交磁束」と称されています。「鎖交磁束」 |
| というのは、 | 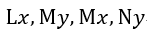 | からわかるように回路側から見た表現であり、磁界(磁場) |
| の「磁束」とは必ずしも一致しません。例えば、磁束 | 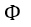 | の磁界(磁場)に直列に接続され同じ |
| 形で | 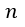 | 回巻回されたコイル(coil)の鎖交磁束 | 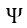 | は、回路面と磁束が直交しているなら |
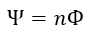 | (15) |
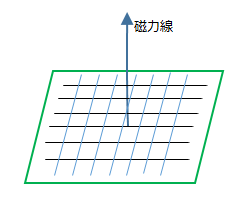 |
| 図1 |
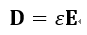 | (16) |
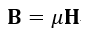 | (17) |