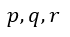
| 流」と称せられているもの)を | 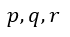 | としておきます。 |
| 物体から切り取った要素 | 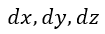 | の面 | 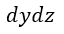 | に現れる電荷量を | 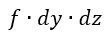 |
| とすると、 | 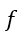 | は | 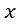 | 軸に平行な電気変位の成分となります。同様に、面 | 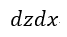 | に現れる |
| 電荷量を | 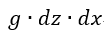 | とすると、 | 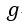 | は | 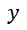 | 軸に平行な電気変位の成分、面 | 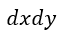 | に |
| 現れる電荷量を | 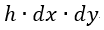 | とすると、 | 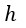 | は | 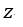 | 軸に平行な電気変位の成分となります。 |
| 電気変位の変化は、我々が | 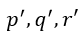 | と称している全電荷の運動を得るために電流 |
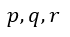 | に加えなければならない |
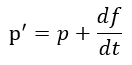 | (1) |
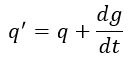 | (2) |
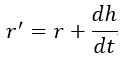 | (3) |
| 起電力の | 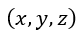 | 成分を | 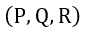 | とする。このとき、 | 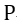 | 、 | 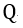 | 、 | 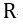 | は与えられた |
| 点のそれぞれ、 | 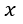 | 方向、 | 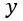 | 方向、 | 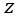 | 方向におかれた導体における単位長さあたりの電 |
| 今、任意の磁石系または電流系による場の任意の点における電磁運動量の | 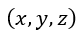 | 成 |
| 分を | 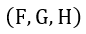 | とします。ここでは、 | 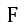 | 、 | 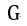 | 、 | 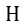 | を、これらの磁石又は電流が場から |
| ぞれ | 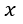 | 方向、 | 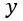 | 方向、 | 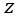 | 方向の起電力の全インパルスを示します。すなわち、 |
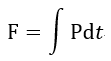 | (4) |
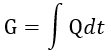 | (5) |
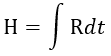 | (6) |
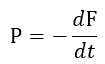 | (7) |
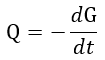 | (8) |
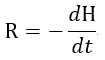 | (9) |
| 今 | 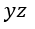 | 面の | 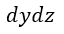 | の微小回路を考えます(図1) |
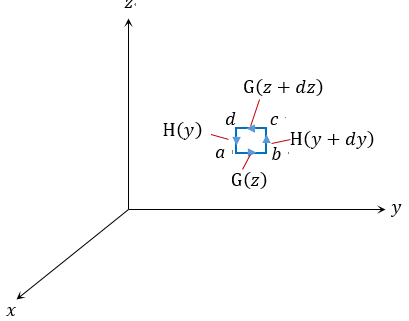 |
| 図1 |
| を加えればいいことになります。そこで、図2のように | 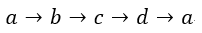 | の一周分 |
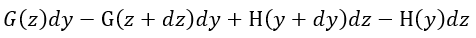 | (i) |
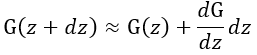 | (ii) |
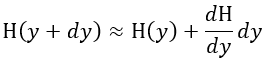 | (iii) |
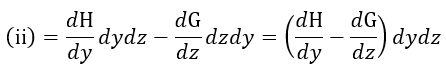 | (iv) |
| これは | 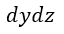 | を通る磁力線の数となります。そして磁力線の方向は | 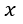 | 方向となります。 |
| 同様に | 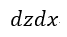 | に対しては | 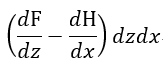 | (磁力線方向は | 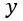 | 方向)、 | 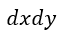 |
| に対しては | 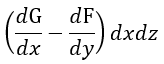 | (磁力線方向は | 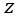 | 方向)となります。 |
| 今、 | 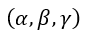 | を単位磁極に働く磁力の | 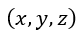 | 成分とします。 |
| ます。そうしますと、 | 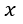 | に垂直な面 | 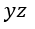 | 内、 | 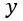 | に垂直な面 | 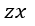 | 内、 | 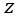 | に垂直な面 | 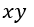 |
| 内の単位面積当たりの磁力線の数はそれぞれ | 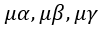 | となります。従って、 |
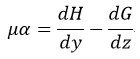 | (10) |
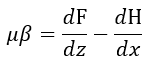 | (11) |
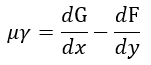 | (12) |
| 今 | 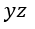 | 面の | 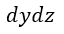 | の微小磁気回路を考えます(図2) |
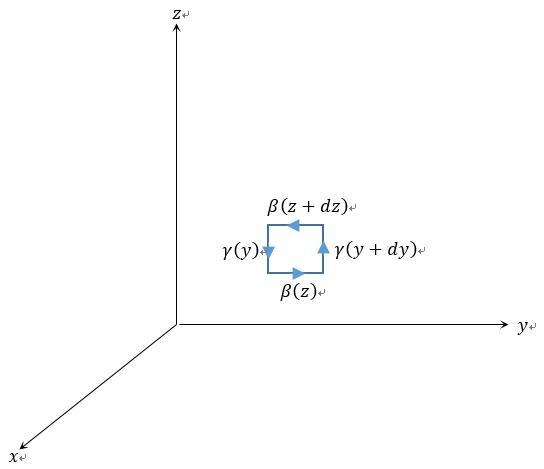 |
| 図2 |
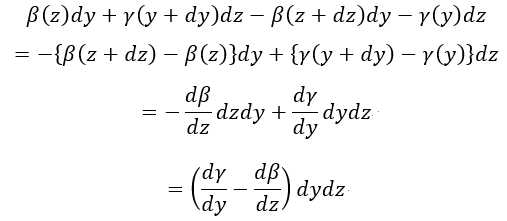
|
| 単位面積あたりは | 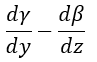 | となります。これは | 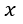 | 軸周りのものです。同様に | 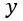 | 軸周 |
| は | 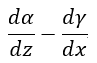 | 、 | 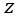 | 軸周り | 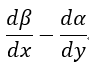 | となります。 |
| ポテンシャル | 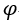 | があり、そのときは | 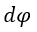 | は完全微分となりますが、Maxwellは |
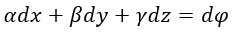 | (13) |
| the difference between successive values of | 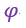 | corresponding to |
| (強さcの完全な電流周りの経路に相当する | 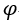 | の連続値間の差は4πcである。) |
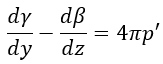 | (14) |
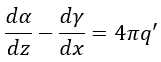 | (15) |
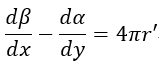 | (16) |
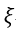 | を回路Aの(誘導)起電力とすると、 |
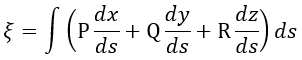 | (17) |
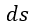 | :長さの要素 |
| 積分は周回積分 | 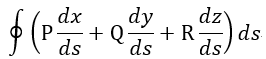 |
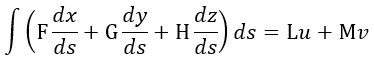 | (18) |
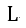 | :回路Aの自己インダクタンス(現代名称) |
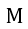 | :回路AとBの相互インダクタンス(現代名称) |
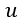 | :回路Aの電流 |
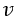 | :回路Bの電流 |
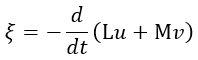 | (19) |
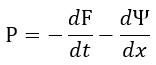 | (20) |
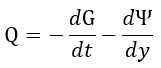 | (21) |
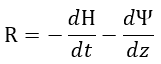 | (22) |
| となるとしているのですが・・・。電気ポテンシャル | 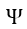 | が突如出現しています。 |
| 説明を読みますと、「 | 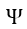 | は | 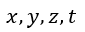 | の関数であり、上記の解に関する限り不定である、 |
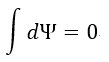 | (v) |
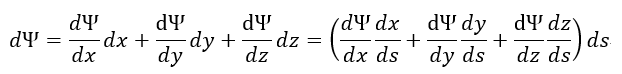 | (vi) |
| (現代表記では偏微分を使って | 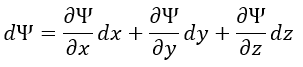 | ) |
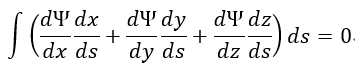 | (vii) |
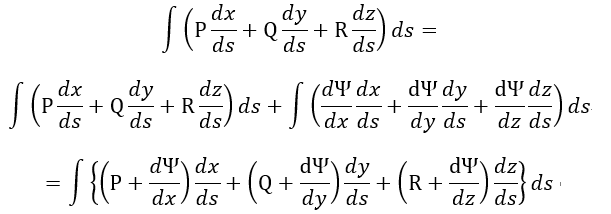 | (viii) |
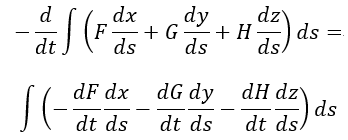 | (ix) |
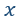 | 軸に平行な長さ | 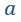 | の短い直線導体を、各成分が | 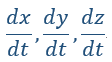 | の速度で動かし、 |
| その両端を速度 | 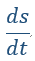 | で二つの平行導体に沿ってスライドさせよう。 |
| 運動導体は、単位時間に、三つの軸に沿って距離 | 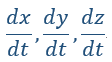 | 移動し、同時に回路に |
| 含まれる平行導体の長さは | 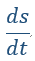 | 増大する。 |
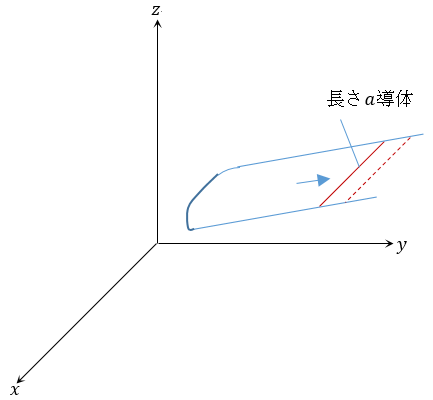 |
| 図3 |
| 電磁運動量成分を | 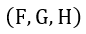 | とすると、回路の全電磁運動量は |
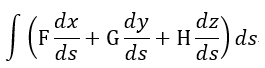 | (周回積分) |
| この長さ | 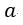 | の導体は常に | 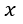 | 軸と平行方向となっており、その方向の電磁運動量成分は | 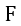 |
| です。常に | 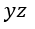 | 面に垂直になっていますので、この導体に関しては | 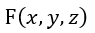 | のみ考え |
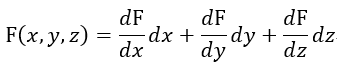
|
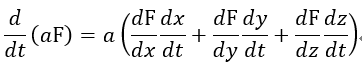
|
| 可動導体が常に | 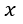 | 軸と平行になるように置かれて、2本の平行導体上をスライドすることで |
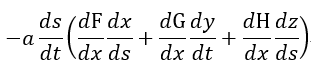
|
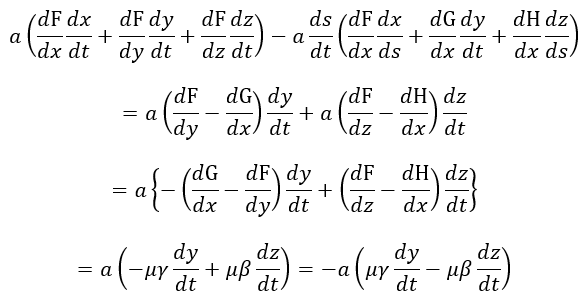
|
| となります。同様にして、長さ | 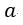 | の導体を | 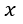 | 軸と平行、 | 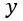 | 軸と平行のときを考えますとそ |
| れぞれ、 | 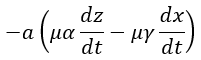 | 、 | 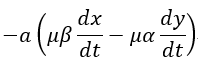 |
| 今、 | 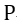 | を | 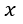 | 軸に平行の可動導体の単位長当たりの起電力とすると、実際の起電力は | 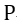 |
| となります。これは前述の電磁運動量の減少分 | 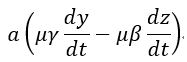 | に等しいので、 |
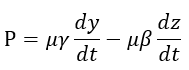 | (x) |
| となります。同様に、 | 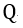 | 、 | 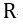 | をそれぞれ、 | 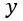 | 軸、 | 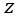 | 軸に平行の可動導体の単位長当た |
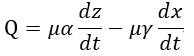 | (xi) |
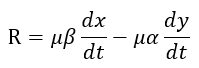 | (xii) |
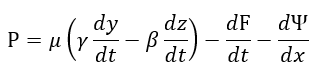 | (23) |
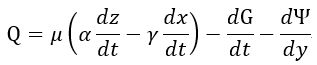 | (24) |
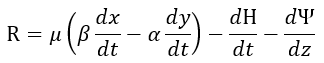 | (25) |
| 起電力を | 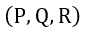 | 、電気変位を | 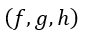 | として、 |
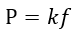 | (26) |
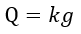 | (27) |
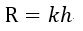 | (28) |
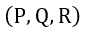 | :単位長当たりの「起電力」ですので、「電界の強さE[V/m]に相当します |
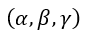 | :磁力(単位面積当たりの磁力線数)「磁界の強さH]に相当します |
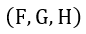 | :電磁運動量、「ベクトルポテンシャルA」に相当します |
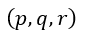 | :導体電流、電流密度に相当します |
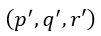 | :全電流、電流密度に相当します |
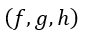 | :電気変位、現在は電束密度と言われることが多いです。Dです。 |