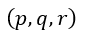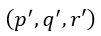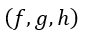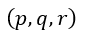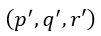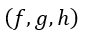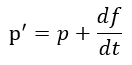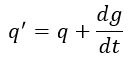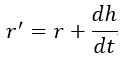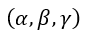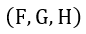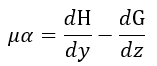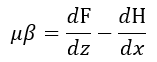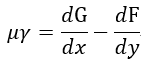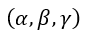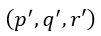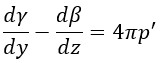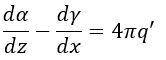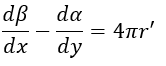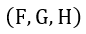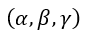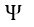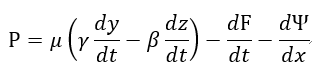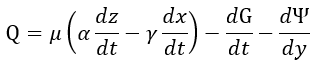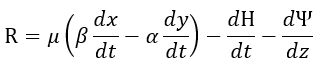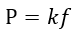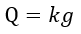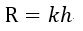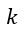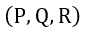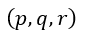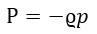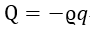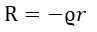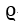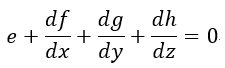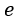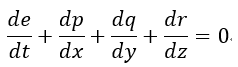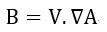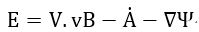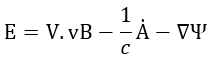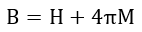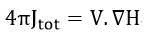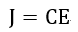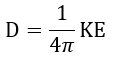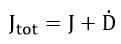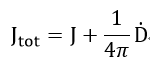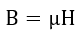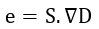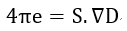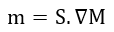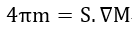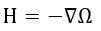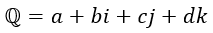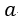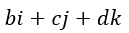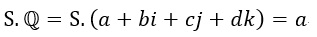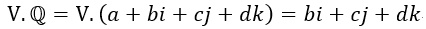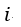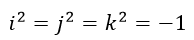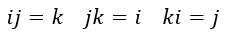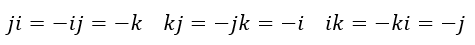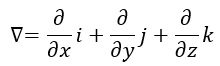となります。
この1873年の方には、1865年のものと異なり、E,H,Bが出てきていますし((28)でBとHの関係も
出ています)、電流は電流密度に代わっています。また、「拡張している」といいましたように1865
年のものにはない概念の(23),(30),(31)が新たに追加されています。
ちなみに、
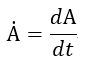 | (39) |
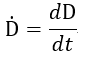 | (40)
|
です。
さて、既に指摘してきましたが、現在、現在『マックスウェルの方程式(Maxwell's equations)』とさ
れている次の四つの方程式群は上記のMaxwell自身が提示したオリジナルの方程式群とは明
らかに異なっています。
この(41)~(44)式の方程式群は、1881年に(クオターニアンに対抗するものとして)、アメリカのGibs
が提案し、「ヘビサイド演算子」などで有名な数学者Heavisideが全面的に協力して1880年代に
確立さ現在一般的に使われている「ベクトル解析法」の適用第一号として、Heavisideが、「ベク
トルポテンシャルA」を測定できないもの(余分なもの)だとして毛嫌いしてMaxwellのオリジナル
式から「数学的に」消去して書き換えたもので、非線形のオリジナル式とは異なり線形で計算
のしやすさから当時の技術系から歓迎され、恐らくは、1890年初頭まで主導権争いをしていた
という「クオターニアン派」に対して有利なデモンストレーションにもなったものと思われ、当時
は"Heaviside-Hertz equaitons"と称せられていたそうです。
で、ここまではこれまで書いて来たのですが、どう数学的に書き換えたのかまでは触れてきま
せんでした。何よりもまず、オリジナル式の存在・その形とそれをHeavisideが書き換えたという
事実が隠され、現在「マックスウェルの方程式」と称せられている(41)~(44)の方程式群をいかに
もMaxwellが作ったかのような事実と異なることが教えられて来たこと、すなわち、私が散々批
判してきている科学界においてなされてきた「真実の『隠匿』」と「『虚構』の流布」がこんな
ところにまで現れていることを示したかったからであり、また、私の調べたところでは意外にそ
の導出まで触れているのを目にしていなかったこともありました。
でもそれでは説得力に欠け、ちょっとお粗末だなと思い、自分で考えて見ました。
まずは下記の表の式の対応を見てください。
1865年版 1873年版 現在の電磁気学での形
----------------------------------------------------------------
|
(1)~(3)式 (27)式 | 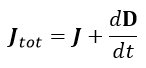 | (45)
|
|
(7)~(9)式 (24)式 | 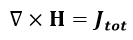 | (46)
|
|
(4)~(6)式 (21)式(+(28)式) | 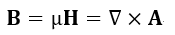 | (47)
|
|
(10)~(12)式 (22)式 | 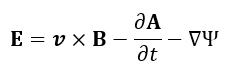 | (48)
|
|
(16)~(18)式 (29)式 | 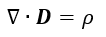 | (49)
|
(41)式は(45)式と(46)式を一つにしただけです。(43)式は(49)式と同一です。
(47)式の両辺の"divergent"(発散)をとると、ベクトル公式より、
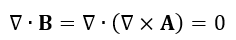 | (50)
|
となり、(44)式が導出されます。
次に、(48)式は、右辺第一項に「回路が動くとき」が含まれていますが、「回路が静止していると
き」は
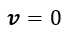 | (51)
|
となりますので、(50)式は、
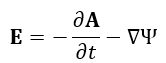 | (52)
|
となります。(52)式の両辺の"rotation"(回転)をとると、
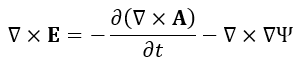 | (53)
|
となります。ベクトル公式より
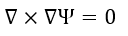 | (54)
|
となりますから、これと(47)式を(54)式に代入すれば(42)式が導出されます。
1865年の式(但し、現在のベクトル解析法で読み替えたもの)から簡単に導出できました。多分、
Heavisideは1873年の論文の中の(21)(22)(24)(27)(29)式を(45)~(49)のようなベクトル解析の式
に変換した上で、このように変換したものと考えます。彼は、数学者ですし、ベクトル解析法の
確立に置いて、クオターニアンとの互換性に腐心していた(結局は完全互換にはできなかった
のですが)くらいですからたやすいことであったと思います。
しかしながら、記事②で言及する予定ですが、この改変は、Maxwellはわざわざ1865年の論文
の中でPARTII「電磁誘導について(On ELECTROMAGNETIC INDUCTION)」として理論化が遅
れていたFaradayの電磁誘導実験結果の理論化ということで一番重点的に論じている部分の
多くをはしょってしまっていると思います。既に述べたように、これはMaxwellの死後になされた
ものであり、Maxwellが10年かけて構築した理論への思いを無視したものであると強く主張した
く存じます。彼の論文の神髄は、磁気と電気を関連付けたもの、1865年では(4)~(12)式、1873
年版では(21)(22)(24)式、今のベクトル解析法表現なら(46)~(48)式にあったと思います。
前回も言及しましたのでもうあまりくどくどと言いませんが、仮想的なものと長く思われてきたベ
クトルポテンシャルの実在性が日本の故・外村博士によって1985年に実証証明されているので
す。そして、その物理的イメージを示していたのは、最初にオリジナル式を構築したMaxwellただ
一人しかいない(それももう約160年も前の1855年の研究を開始した頃の最初の論文で示してい
るのです!そういうこれまで隠されて来た史的事実をしっかりと知っておいて欲しいと思います。
ま、Heavisideの嫌ったベクトルポテンシャルはものの見事にスカラーポテンシャルとともに消し
去られていますが、単にクオターニアン表記しただけでなく拡張されている(方程式が増えて11
個にもなっている)1873年版の拡張方程式群はともかく、最初の1865年版に対しても、「回路が
動くとき」は無視されていますし、ベクトル解析法で読み替えた
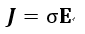 | (55) (オームの法則の拡張版) |
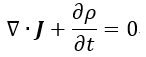 | (56)
|
が省略されています(もっとも、(56)式はなぜか1873年の方程式群には抜けていますけれども)。
そもそも、Maxwellは1865年の論文で示した成分表記で20個の式を「電磁場(界)の一般方
程式(General Equaitons of Electromagnetic Field)」
と称しています。Faradayの実験結果を含めての電磁界現象の集大成の方程式群という思い
が込められています。ですから、省略された条件や式があるということはそういうMaxwellの思
いを無視したものであり、誤解さえされている今、私は(41)~(44)を「マックスウェルの方程式」
と呼ぶのはおかしいと思っています。以上の史実から、(41)~(44)の方程式群は、複数の海外
サイトで目にした名称"Maxwell-Heaviside equations"という呼称が一番的確
ではないかと私は思っています。
ところでお聞きしたことなんですが、とりあえず現在の『マックスウェルの方程式』はオリジナル
のものを書き換えたものであることには言及しているものの、「(オリジナル方程式群には)余分
なものが入っており、Hertzがすっきりさせたのが現在の『マックスウェルの方程式』である」と
いう史実とは異なることが記載された電磁気学の教科書があるそうです。教科書に書くのなら
きちんと史実を調べて書いていただきたいものです。著者は意図的ではないと思いますけど、
この記述ははっきり言って「嘘」です。
もう一度、史実をきちんと書きますと、
アメリカのGibsが創案し、1880年代にHeavisideが全面協力して確立され、現在一
般的に使用されている「ベクトル解析法(vector analythis)」を、1840年代に
Hamiltonが創設し、Maxwellの友人のTaitという方が発展させていた「クオターニ
アン(quaternion/四元数)」派との争い(1990年代まで続いた)の中で勝利をおさ
めて一般使用化すべく図られたデモンストレーションとしての適用第一号として『数
学的に』ベクトルポテンシャルAと合わせてスカラーポテンシャルΦを消去した形に
書き換えたのがずばり、現在「マックスウァルの方程式」と称せられているものであ
る(※1)
です。これはヨタ話などではなく、複数の海外サイトで言及されているものです。そして、これも
複数のサイトで示されていましたが、当時、上記(41)~(44)の方程式群は"Heaviside-Hertz
equations"と称せられていたことも(※1)の史実を補強するものであり、したがって、Heaviside
に言及していない上記の先生の教科書記述の誤りは明白です。
これは推測ですが、Einsteinが1905年の例の相対性理論の論文"ON THE ELECTRODYNA-
MICS OF MOVING BODIES"の中で、"Maxwell-Hertz equations"と称している(調べた
限りではこの呼称はこれ以外見当たりませんでしたのでEinsteinの独自呼称の可能性もありま
す。Einsteinはイギリスでの講演の中で「私はNewtonより、Maxwellにより影響を受けている」と
述べているそうですから、そんなことでこういう呼称をしたのかもしれませんが、Heavisideの名
前を消してしまってHertzの名前だけ残した理由はよくわかりません)ことにある気がしています。
"Heaviside-Hertz equations"と称せられていたのは、Hertzは独自にMaxwellのオリジナル式の
切りつめを検討していたという事実があり、また、Hertzは1887年に、そもそもは先にFaradayが
予測していて(前回記事参照)Maxwellが1865年の論文の中で自らのオリジナル式から理論的
に証明したものの当時の科学界からは賛同されてこなかった「電磁波」の実在性を実証試験で
証明したこと、そして権威科学者であったことなどから敬意を表してつけられたのではないか(
科学界では往々にしてそういうことがあります。例えば、熱力学の第二法則として日本ではケル
ビンの法則と呼称されているものがありますが、欧米では"Plank-Kelvin's Statement"と称され
実際にはケルビンとは関係なく、"Plank's Statement"であり、権威付けでKelvinの名前が付属
されたそうです。ここでも日本では学徒を誤解させる「虚構」があります。)と推測しますが、(※1)
が史実であり、直接この方程式を導出したのは間違いなくHeavisideですから、Einsteinはそうい
う事実を知らなかったのかもしれません。恐らく、大変失礼ながら著者は、このEinsteinの呼称
と、当時の状況を中途半端に解釈して誤解した人-Einsteiniansは往々にしてそういうことをし
てきた史実があります-(ひょっとすると意図的かも)が書いたものを読まれたか、誰かにそう聞
かれたものと思われます。
Maxwellの著書論文において、その難解さから論文編集者からも批判を受けたのは、1873年の
拡張版の"Treatise on Electricity and Magnetism"(クオターニアン表記)のものであり、こちらは
Maxwell自身も批判を受けて自ら切りつめ化に取り組み、残念ながら彼はそれを世に出す前の
1879年に40代の若さで病死されていまいましたが死後の1881、1882年に意思を継いでそれぞ
れ改定第一版、第二版として出されています(ちなみにBeardenという退職米軍将校で在野の
異端科学者のBeardenという方は1873年のものが価値があると力説されているよですが)。そし
て一方でHertzも独自にこれの切りつめ化を図っていたという事実はあります。ただ、ベクトルポ
テンシャルを毛嫌いし「余分なもの」と考えたのはHeavisideであり、Hertzではありません。その
上、当時まだベクトル解析法はできたばかりで一般認可されてもいなかったことも勘案すれば
「よぶんなものがありHertzがすっきりさせたもの」というのは史実に反するのは明白です。
----------------------------------------------------------------------------
(追記)('17/8)
1873年の"Treatise on Electricity and Magnetism"の中でMaxwellは次のように書いているそ
うです。
"We shall not, however, expressly introduce Quaternion notation. …
In this treatise we have endeavored to avoid any process demanding
of the reader a knowledge of the CalculusofQuaternions"
「我々は、しかしながら、明白にクオターニアン表記法を導入しないつもりである。
この論文では、我々はクオターニアン計算を読者に要求するプロセスを避ける
べく努めた。」
Polar and axial vectors versus quaternionsというウェブ論文に、「クオターニアン計算と座標計
算を使っている」と書かれていましたが、どうやら、「表記法」にクオターニアン表記を採用した
というだけなのかもしれません。1865年の論文での三軸座標表現の最初のオリジナル式と比
べてみても、"pure quaternion"(V.という部分)にそのまま移行させている感がしていますから。
拡張した部分はどうもクオターニアン演算子法による追加導出ではなさそうです。
(この稿続く)
('17/7)
目次に戻る
次へ
|
|