紋章や魔方陣で、以下のような図形が、五芒星(ペンタグラム/pentagram)、六芒星(ヘキサグラム/hexagram)の名でお馴染みなのではないかと思います。

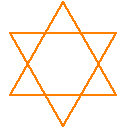
これらは幾何学関連では「星型多角形」と呼ばれており、それぞれ「星型五角形」「星型六角形」とも呼ばれます。
五芒星は「5/2角形」、六芒星は「6/2角形」に相当しています(六芒星の方は後述の注意点がありますが)。
この分母の部分は「密度」と呼ばれています。
七芒星(星型七角形)の場合、以下のように2種類存在しています。
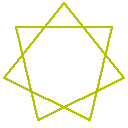

それぞれ、「7/2角形」「7/3角形」に相当しています。
八芒星も2種類存在し、九芒星となると更に増えて3種類となります。
まとめると以下のようになります。

このように、角の数が2つ増える毎に1種類増える形となっています。
4/2や6/3の箇所にあるなりそこない的なものを0.5個と考えれば、
角の数が1つ増える毎に0.5種類増える形となります。
なお、このなりそこない的なものは、上表だと線分の複合で表現してますが、
これは「正多角形の頂点を特定の数飛ばして結ぶ」という方法の場合に現れるもので、
「degenerate star polygon」(直訳すると「退化した星型多角形」)と呼ばれているようです。
後述の星型化で作成した場合は以下のように、無限に伸びる平行線のペアの複合になります。

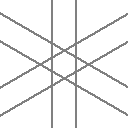
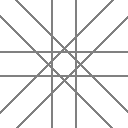
これを無限に縮めたものが、上表の線分の複合であるという見方もできます。
上表の内、6/2→3/1、10/4→5/2のように約分ができるものは、以下のように複数の多角形に分解できます。
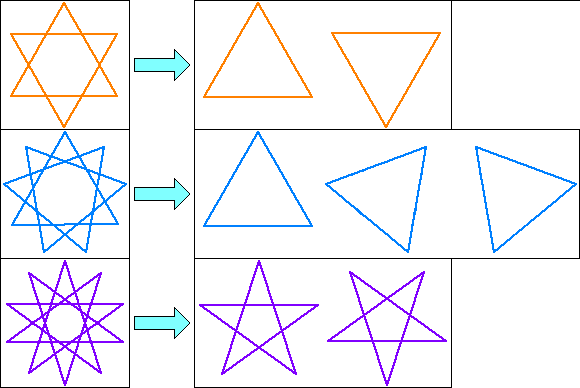
このように、複数の多角形に分解できるタイプのものは「複合多角形」と呼ばれてます(正式な用語であるかは怪しいですが)。
文脈によっては、通常の多角形(凸多角形)も星型多角形に含めるかのように書かれている場合がありますが、
「最初の星型」という表現した場合は、七角形なら7/2角形を意味するので、
本稿ではあくまで通常の多角形は星型に含めないという解釈を取ります。
前述の通り、星型多角形には複合多角形が含まれていますが、
どうもこういうタイプは多角形そのものに含まれないようです。
「星型多角形」という表現だと多角形の一種であるかのようになってしまい、混乱の元になってないか気になる所です。
英語を見てみると、星型多角形にあたる表現は「stellated polygon(またはstellating polygon)」となっています。
これは「多角形を星型化したもの」という意味合いであるため、多角形の一種とは限らないと取ることができます。
この「stellated~」という表現は、三次元版である星型多面体で特に多く用いられています。
一方で「star polygon」という表現も存在します。
こちらの意味合いは「星型の多角形」となり、多角形の一種という意味合いが強くなっており、
実際に複合していないタイプのものに限定している様子があります。
ただ、三次元版の「star polyhedron」共々、定義がどうも定かではないようです(「交差がある」と同義の場合もあるようです)。
このタイプの表現が用いられる例は希少ですが、後述の星型正多角形にあたる英語は「regular star polygon」となっており、
他には三次元の場合の「regular star polyhedron(星型正多面体)」「uniform star polyhedron(星型一様多面体)」があります。
星型一様多面体については星型化では得られないタイプのものが多いため、
「stellated polyhedron」とは二次元の場合よりも更に大きな意味がズレができています。
結局、この「stellated polygon」と「star polygon」という異なるものを、日本語では共に「星型多角形」としてしまっているのが、
問題の元になっているのではないかと思います。
星型多角形は、「星型化多角形」「多角形の星型」と呼んだ方が妥当かもしれません。
「多芒星(芒星図形/ポリグラム/polygram)」という名を流用する手も考えられますが、
以下のようなクロウリーの六芒星や性格論における九芒星(エニアグラム)の例がある辺り、逆に意味が広くなり過ぎる可能性がないかが気になる所です。

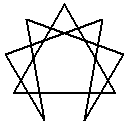
「複合多角形」という表現にも同様の問題があるので注意が要ります。
英語だと「compound polygon」とも呼ばれますが、正式な場では「polygonal compound」(多角形の複合)といった
表現が用いられる傾向にあるように見受けられます。
こちらについては、無難な表現としては「複合化多角形」「多角形の複合」「多角形複合体」がありそうです。
全ての角と全ての辺の長さが等しい多角形は正多角形と呼ばれますが、
星型多角形に対しても「星型正多角形」が存在します。
ただし、星型正多角形と呼ばれるためは、辺と角が等しいことに加えて、
複合多角形に該当しないことが明確な条件として挙げられています。
そのため六芒星は、2つの三角形の複合であるため、辺と角が等しくても星型正多角形には含まれません。
違和感があるかもしれませんが、いわゆる星型多角形がstelleted polygonであるのに対し、
星型正多角形はregular star polygonであり、日本語名は似てても根本的に別物となりそうです。
そして複合多角形である六芒星はそもそも、多角形そのものに含まれないらしいのです。
そのため六芒星は、星型正六角形とも呼ばれないようです。
先程の「6/2角形」という表現も不適当そうです(こちらについては、6/2=3となってしまう時点でまずい様子です)。
では、星型正六角形に相当する図形は何と呼べば良いのかが問題になります。
「2つの正三角形による正複合」という表現はできますが、無駄に長い感がないですかね。
正式かどうかはわかりませんが、「正六芒星」という表現が妥当だと思います。
「等辺六芒星」という表現も存在するようですが、
「全ての辺が等しい」というだけでは以下の場合も当て嵌まってしまう点に注意が要ります。
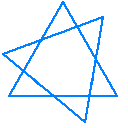
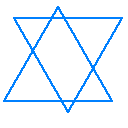
「regular star polygon」という呼称自体、定義が定かではない「star polygon」をベースとした名前なのが微妙な気もします。
この図形は結局、正多角形から「凸型」という条件を省くことで現れる図形なので、
幾何学的用語としては「非凸正多角形(non-convex regular polygon)」と呼ぶか、
または「星型=交差」とする立場から「交差正多角形(self-intersecting regular polygon)」と呼ぶのが妥当なように思います(味気は無いですが)。
星型多角形に相当するものは三次元空間上にも存在し、「星型多面体」と呼ばれています。
代表的なものとして、以下の星型八面体と星型正多面体シリーズがあります。
 |  |  |
星型八面体
(正八面体の唯一の星型) | 小星型十二面体
(正十二面体の最初の星型) | 大星型十二面体
(正十二面体の最後の星型) |
 |  |
大十二面体
(正十二面体の2番目の星型) | 大二十面体
(正二十面体の星型の一種) |
こちらも、英語ではstellated polyhedron(星型化された多面体)という呼ばれ方をします。
上記の星型八面体は、正四面体2つによる複合多面体となっていますが、こちらも多角形の場合と同様、
多面体扱いされない様子があるので注意です。
多角形から星型多角形を、多面体から星型多面体を作成する操作は「星型化(stellation)」と呼ばれます。
この星型化という操作は、具体的には下図のように、多角形なら各辺を、多面体なら各面を伸ばして行き、
その交点によって新たな多角形を作成する操作となっています(他にも色々ルールがあるようです)。
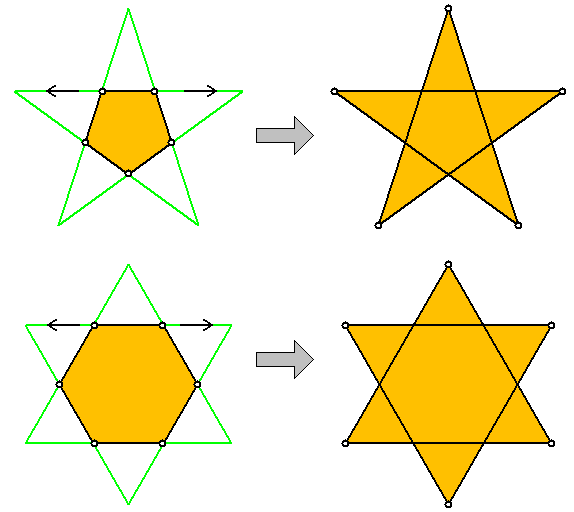
一方、手で星型多角形を描く場合は、多角形の頂点を一定数飛ばしに結ぶ形で描くと思います。
こちらのような方法は「ファセッティング(faceting/facetting)」と呼ばれています
(この言葉は一般的には、宝石を磨く意味として用いられているようです)。
正多角形の場合はどちらでも同じ図形ができますが、多面体の場合はそうはならない点に注意が要ります。
以下は正十二面体を星型化しているイメージのアニメーションpngです。

多面体を星型化を論じる際には、以下のような図がよく出てくると思います。

この図は「stellation diagram」と呼ばれています。
和名は不明ですが、直訳すれば「星型化線図」になると思います。
自動翻訳だと「星型図」となったりしてますが、探した限りではこの意味での用例は見つかりませんでした。
そしてこの図は、多面体の特定の面の延長面と、他の全ての面の延長面との交線の図となっており、上図は正二十面体の場合の星型化線図となります。
なお、正八面体と正十二面体の場合は非常にシンプルで、以下のようになります。


以下は、イメージをつかむ一助等のため、この線図と元の図形を組み合わせてみたものです。



先程の星型多面体の例の内「小星型十二面体」「大星型十二面体」「大十二面体」は、正十二面体の星型ですが、
この星型化線図を用いて以下のように対応付けられます。
|
星型化線図 |
立体 |
| 普通の正十二面体 |
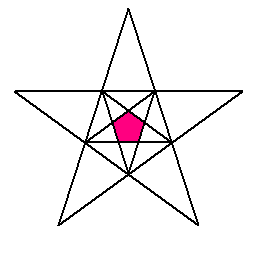 |
 |
| 小星型十二面体 |
 |
 |
| 大十二面体 |
 |
 |
| 大星型十二面体 |
 |
 |
星型多角形は、元の多角形の角数が2つ増える毎に1つ増えるという、不規則な増え方をしていましたが、
球面幾何学上においては、1つ増える毎に1つ増えるという規則的な増え方をし、
三芒星や四芒星も考えることができます。
以下はそれをステレオ投影したものとなっています。
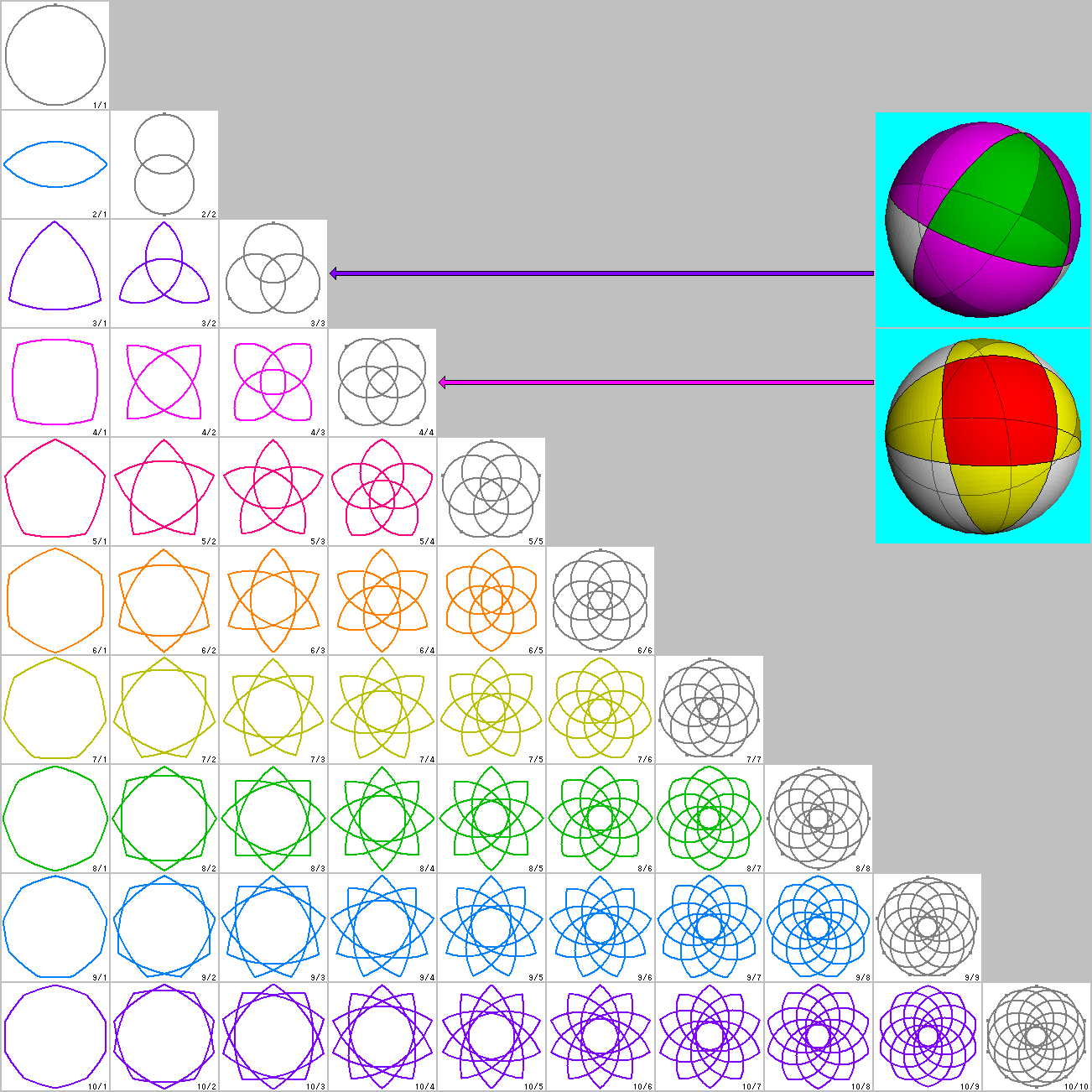
詳しくは「球面幾何学上の星型」で記載します。
以下は、ルーローの多角形の描き方を星型多角形に対して用いてみたものです。
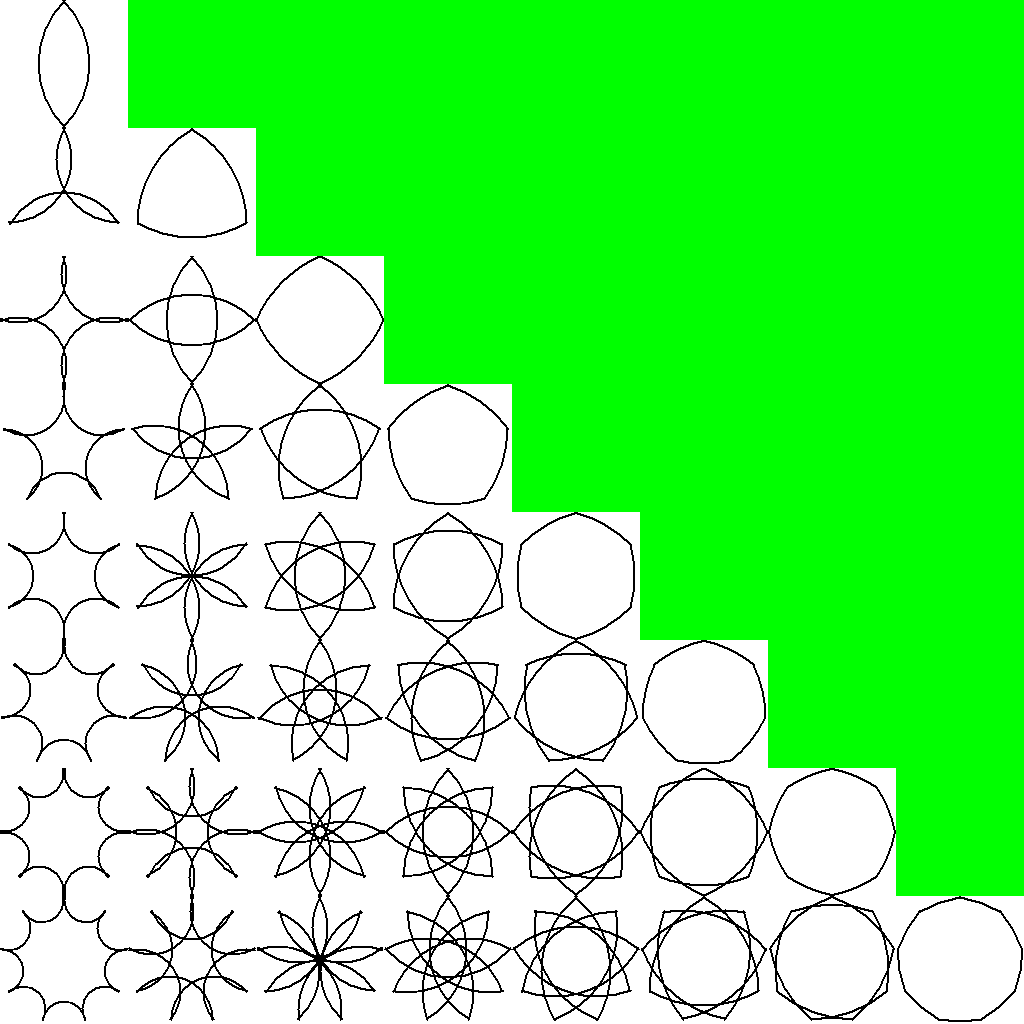
球面幾何学上の星型多角形とはまた別物ですが、こちらも元の多角形の角数が1つ増える毎に1つ増えます。
ルーローの多角形であるためには定幅図形である必要があるようなのですが、これはそれには当て嵌まらないので、
ルーローの星型多角形やルーローの多芒星と言った呼び方はできなさそうです。
仮に花芒星(flower polygram)と呼んでいます。
(2009.10.19)
2017.6.4-2025.9.20
































