球面幾何学上では以下のように、三芒星(trigram?)や四芒星(tetragram?)も考えることができます。


簡単のためにそれぞれステレオ投影で表現すると、以下のようになります。
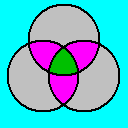
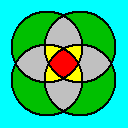
ユークリッド幾何学の場合は、星型多角形・星型多面体の紹介で触れたように、
星型多角形の種類は、角の数が2つ増える毎に1つ増えました。
しかも、偶数角形ではなりそこないのようなものが現れるという、少々複雑な様相となっていました。
これに対し、球面幾何学上の場合は、角が1つ増える毎に星型も常に1つ増え、
まとめると以下のような綺麗な表となります。
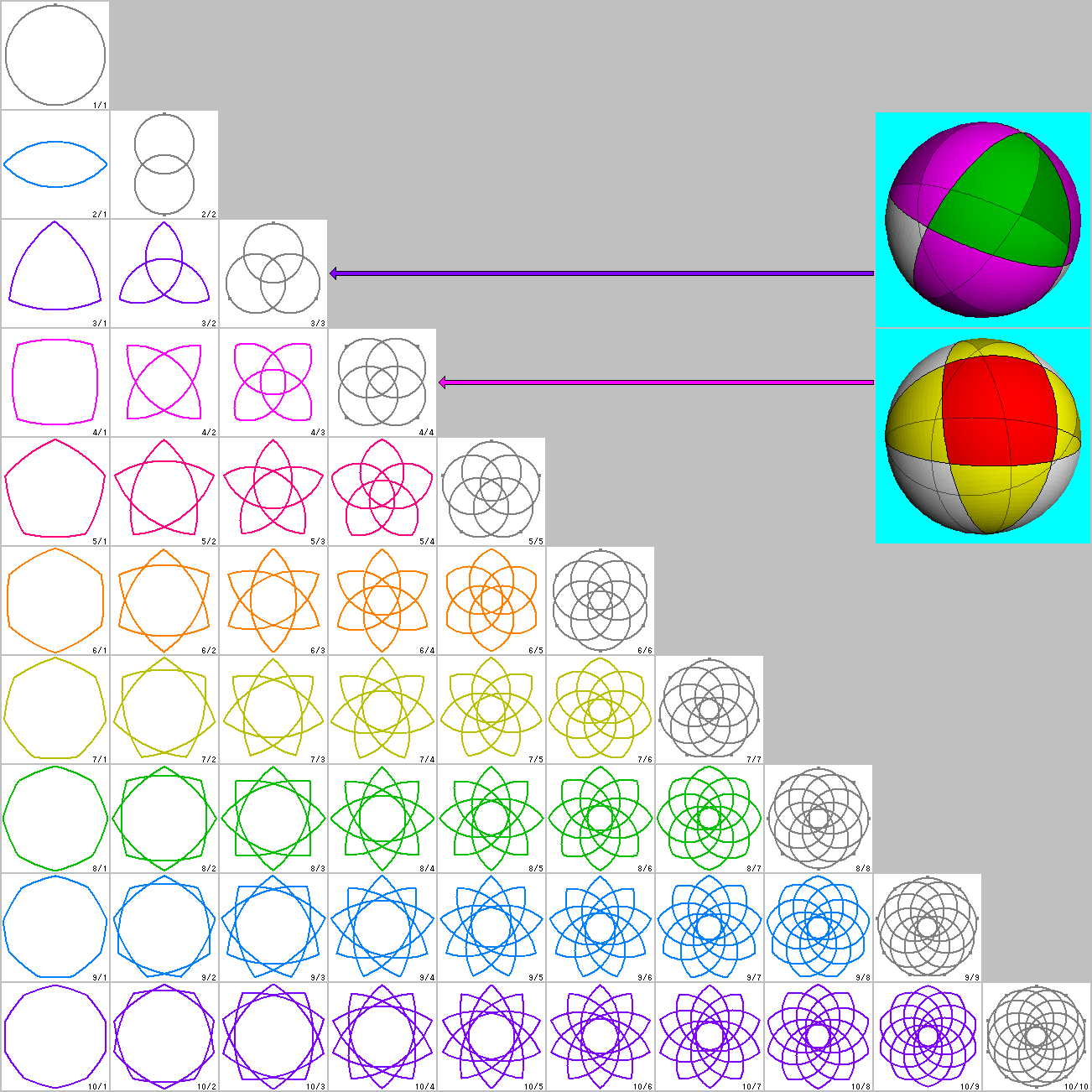
こういう見方は、通常の平面での星型化を考える上でも、役に立つのではないかと思います。
正四面体や立方体に対しては星型を作る事はできませんが、
こちらも球面幾何学上(三次元の場合ならば四次元超球面上で考える)においては、
シンプルな形で星型を見出す事ができます。
以下は立方体における例で、言わば星型立方体(stellated cube?)あるいは星型六面体(stellated hexahedron?)と呼べそうなものです。
| 何番目の星型か |
形状の概略説明 |
全体像 |
一つの面のみを取り出したもの |
Stellation diagram(星型化線図?) |
| 0 |
立方体 |
 |
 |
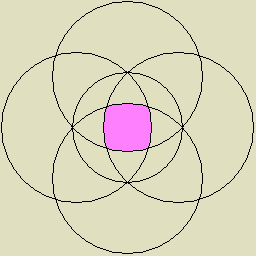 |
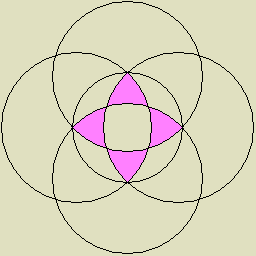
| 1 |
4つの二角形で構成された四面体3つの複合 |
 |
 |
 |
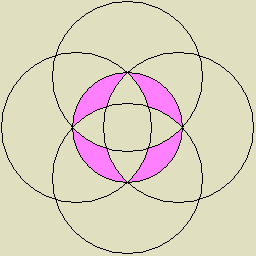
| 2 |
一角形で構成された二面体3つの複合 |
 |
 |
 |
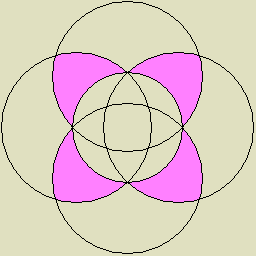
| 3 |
6つの球面幾何学的な4/3角形で構成された、球面幾何学的な星型正多面体 |
 |
 |
 |
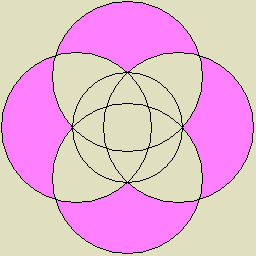
| 4 |
6つの正方形を交差させて構成された球面幾何学的な星型正多面体、あるいは、一角形で構成された二面体12個の複合 |
 |
 |
 |
| 5 |
立方体、あるいは一面体6つの複合 |
 |
 |
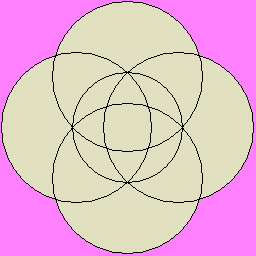 |
ここで、星型化線図も球面上に描いた方が正確となり、それが次の図となります。

心射投影は、投影結果も直線になるという性質があります。
これを利用し、球面幾何学上の星型を平面に投影すると、表面の分は通常の星型と同じになります。
そして以下のように、表と裏の2つの世界のペアによって表現される形となります。
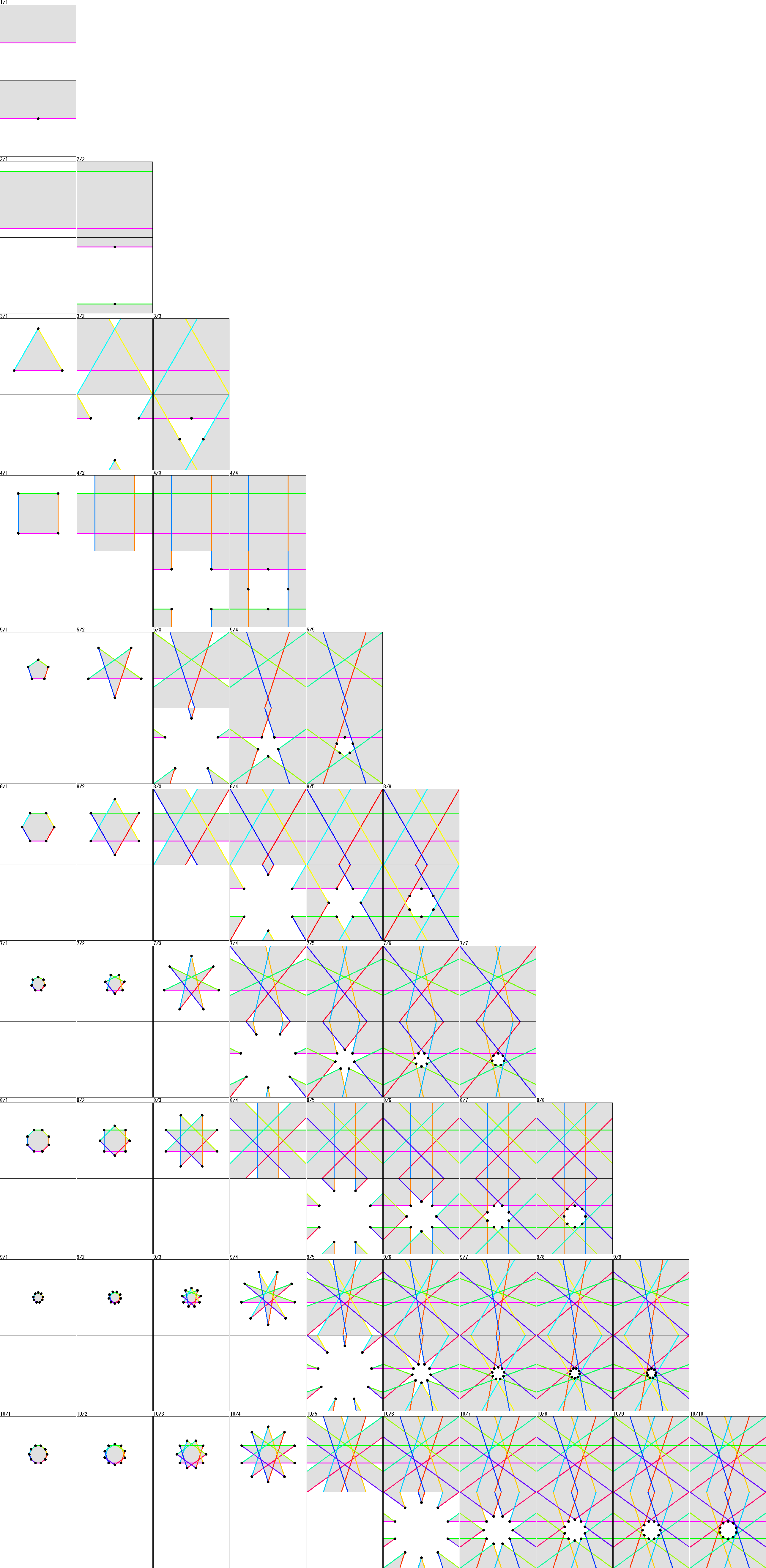
同じ色の線が、表でも裏でも同一の線であることを意味しています(色の違いが微妙なものも多いですが)。
球面幾何学の世界では、ユークリッド幾何学上では現れなかった星型も表せましたが、
逆に双曲幾何の世界では、ユークリッド幾何学上で現れる星型も表せない場合があります。
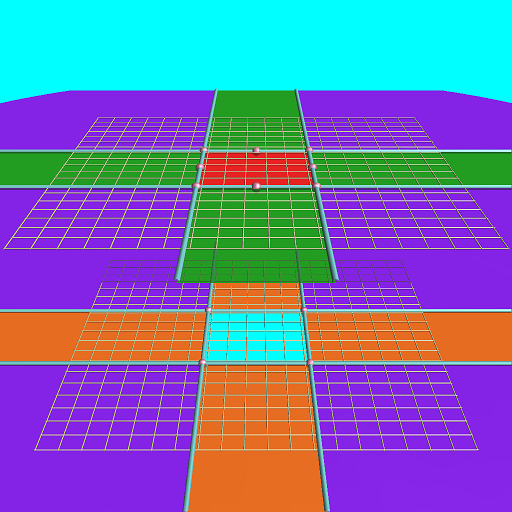
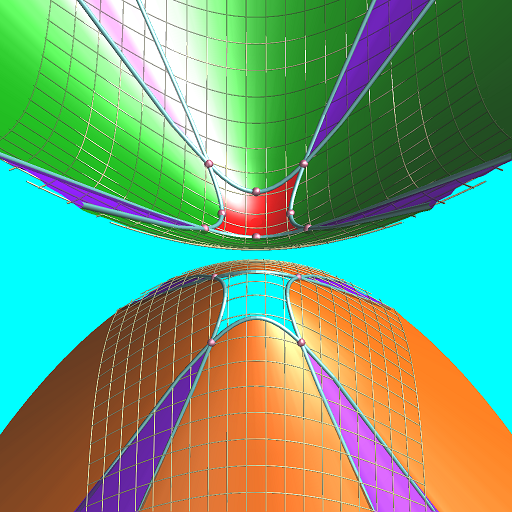
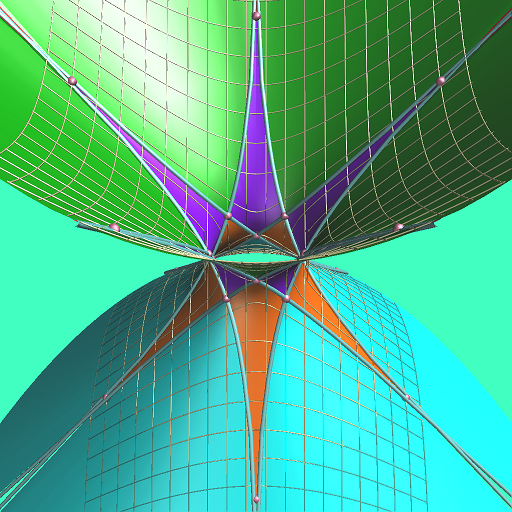
そして先ほどと同様に、球面幾何学上の星型を双曲幾何学上の直線で表現しようとすると、
以下のように、二葉双曲面の表裏分と一葉双曲面との合計3つの「葉」が必要になりそうです。
二葉双曲面の方が、先ほどの2枚の平面に相当し、これに一葉双曲面が加わった形となります。
ここで、二葉双曲面の方はzが虚数ですが、一葉双曲面はxyが虚数、zが実数となってます。
|
球面 |
ユークリッド |
双曲 |
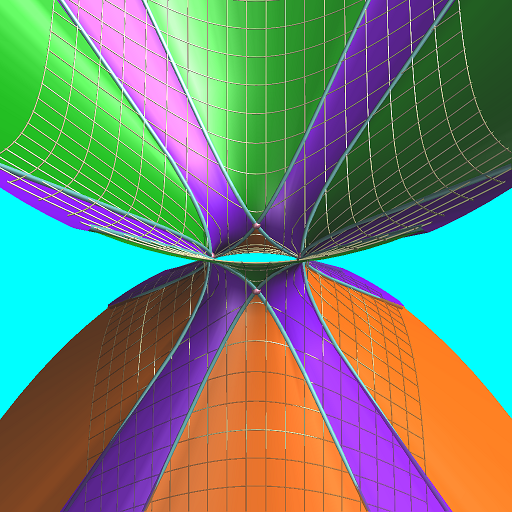
| 四角形 |
双曲の場合でも頂点が有限範囲 |
 |
 |
 |
 |
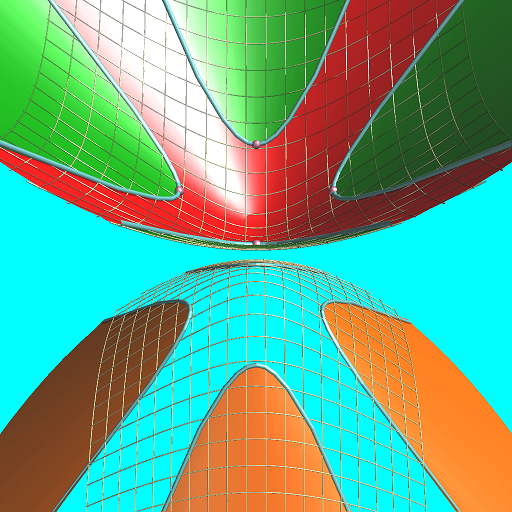
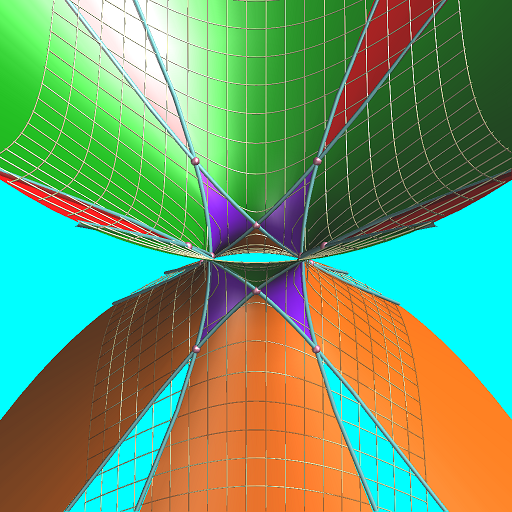
| 双曲の場合は頂点が無限遠 |
 |
 |
 |
 |
| 双曲の場合は辺も無限遠 |
 |
 |
 |
 |
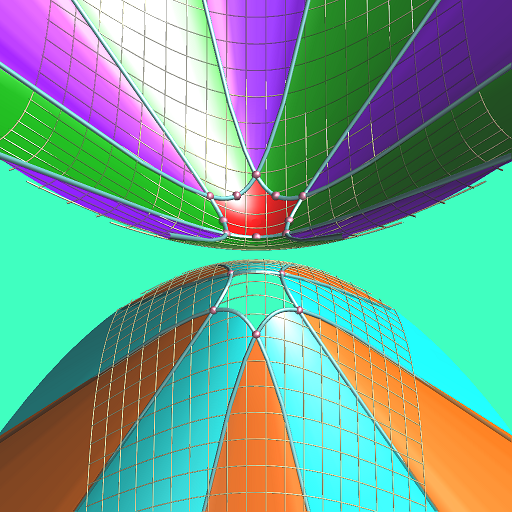
| 五角形 |
双曲の場合でも頂点が有限範囲 |
 |
 |
 |
 |
| 双曲の場合は頂点が無限遠 |
 |
 |
 |
 |
| 双曲の場合は辺も無限遠 |
 |
 |
 |
 |
2017.6.4-2021.3.5
星型多角形・星型多面体の紹介
















































