そして双線分錐にあたる図形(斜凧形と呼んではどうかと思ってます)の、4つの要素の組み合わせで表現できます。
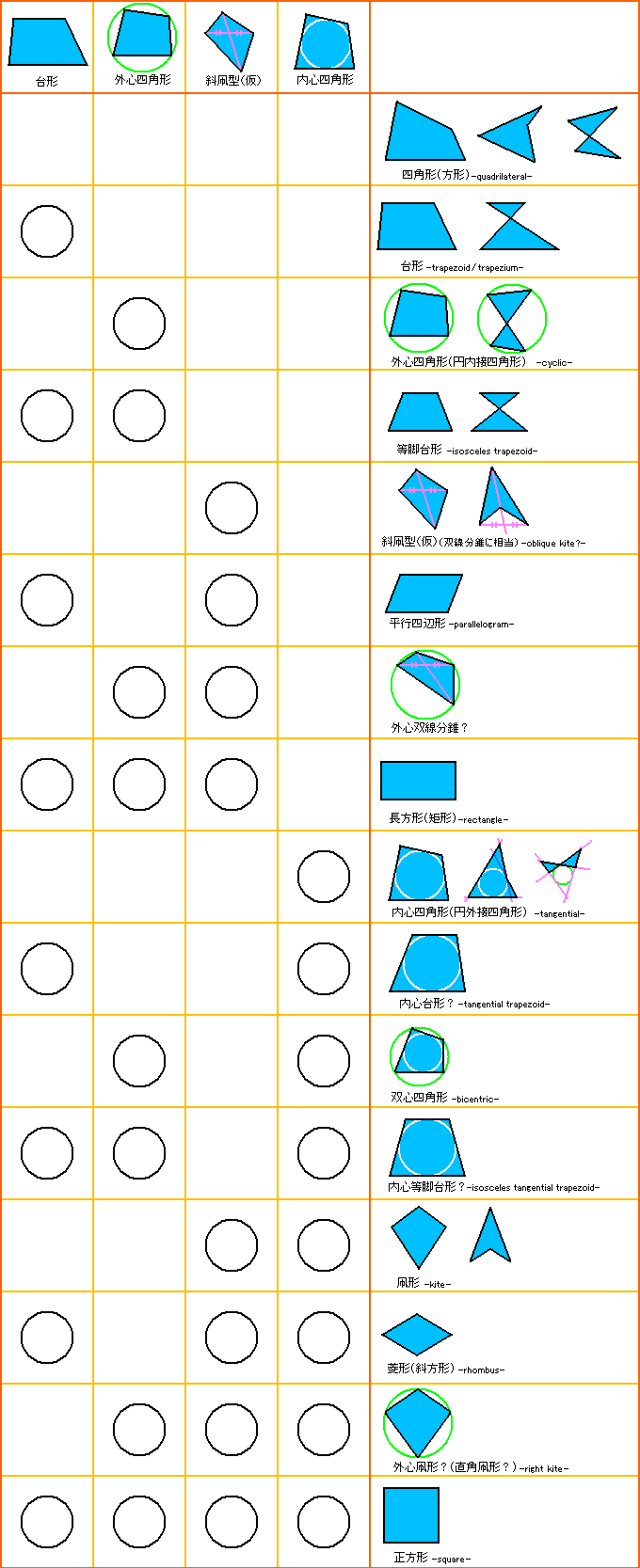
他の四角形を用いても同様の表現ができますが、多分これが最も基本形になるかと思います。
四角形の4bit式分類
斜凧形
その他の台形の双対候補
傍心四角形
主要な四角形は以下のように、台形、外心四角形(円内接四角形)、内心四角形(円外接四角形)、
そして双線分錐にあたる図形(斜凧形と呼んではどうかと思ってます)の、4つの要素の組み合わせで表現できます。

他の四角形を用いても同様の表現ができますが、多分これが最も基本形になるかと思います。
双対図形の考え方により、台形と以下のように結びつきます。
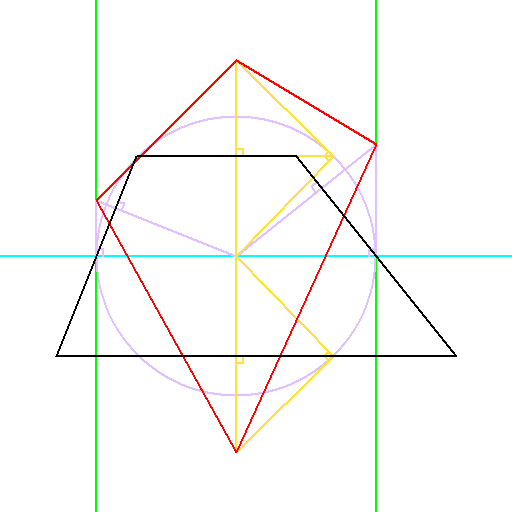
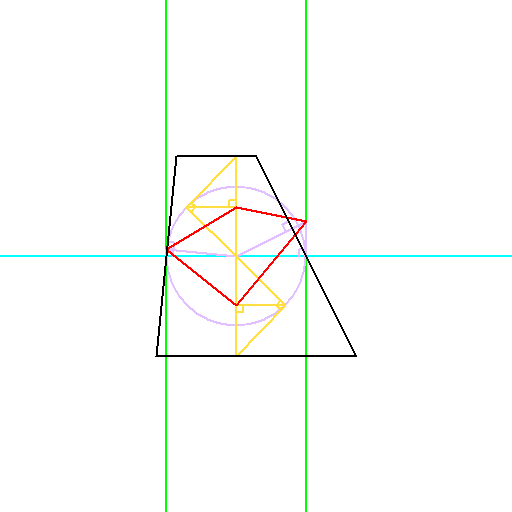

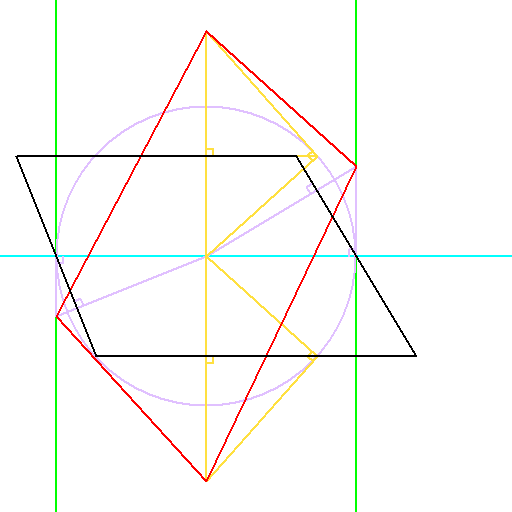
台形、外心四角形、内心四角形と、もう一つ何を四角形の4番目の要素として考えるべきか、
長い間悩んだのですが、この図形は双角錐の二次元版にあたり、
かなり基本的な図形と言えるので、恐らくこれが妥当なのではないかと思います。
読み方は「しゃたこがた」では苦しいと思いますが、「凧」は国字らしく音読みは本来無いので、
「しゃたこけい」を崩して「しゃたっけい」、または「巾」の音読みを無理矢理あてて「しゃきんけい」はどうかと思います。
英語は「oblique kite」辺りはどうかと思います。
ただ、球面幾何学上で台形をどう定義するかが問題かもしれません。
また、後に紹介する2つの候補と異なり、3つの辺の長さが決まっても、4つ目の辺の長さは決まりません。
四角形の4つの要素として、台形を用いるべきかどうかという問題もありますが、
台形を用いるとしたら、残りの一つはその双対になるはずだとうことで、
斜凧形の前に考えたものが以下となります。
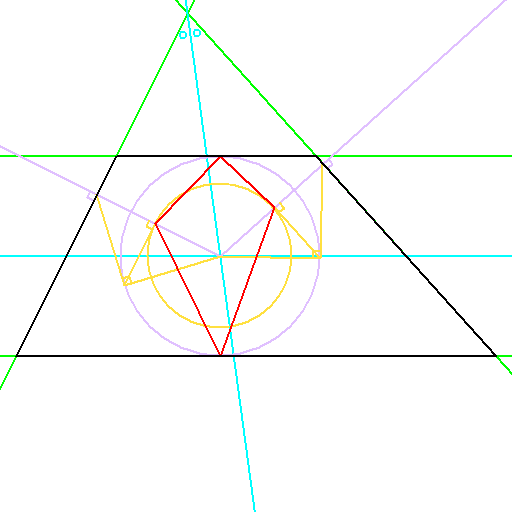
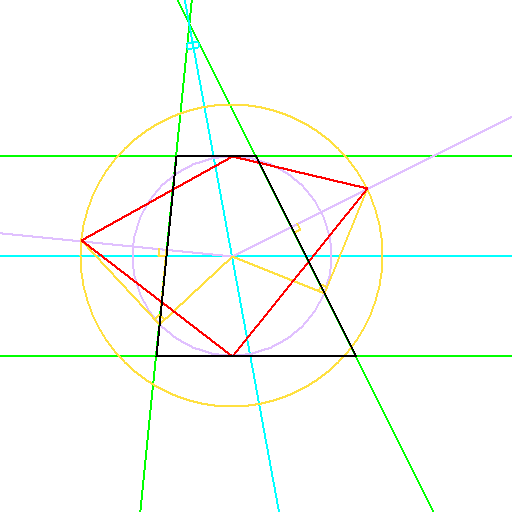
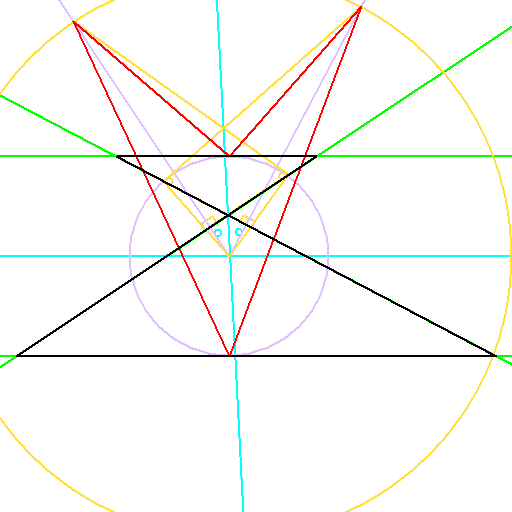
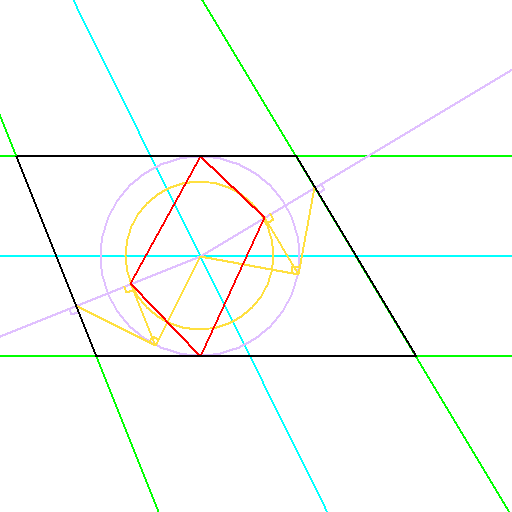
球面幾何学上で台形をどう定義するかから考え、
2組の対辺を延長した交点の、角の二等分線の交点を双対の中心とする考え方です。
対角線ACの中点をPと置いて、PB=PDとなるような四角形ABCDとなります。
式は、辺abcdがa2+b2=c2+d2という、結構綺麗な形となります。
どちらの角を二等分するかによって以下のようになり、これは内心四角形と傍心四角形の関係と同質であると思います。
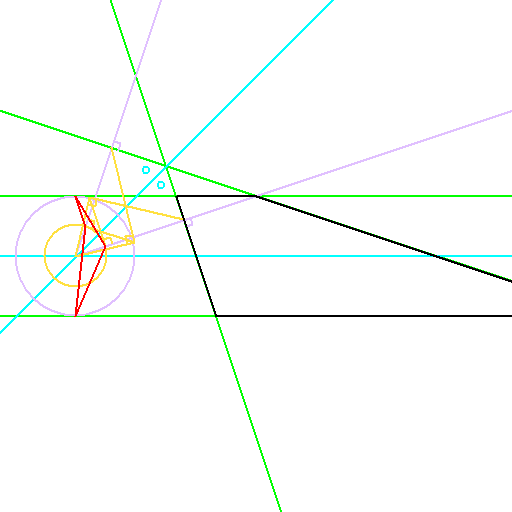
四角形の4つの要素の候補として、傍心四角形も考えていました。
始まりは、台形ABCDの角がA+B=C+Dを満たしているので、
これに対して、辺abcdがa+b=c+dを満たす四角形はどうかと考えました。
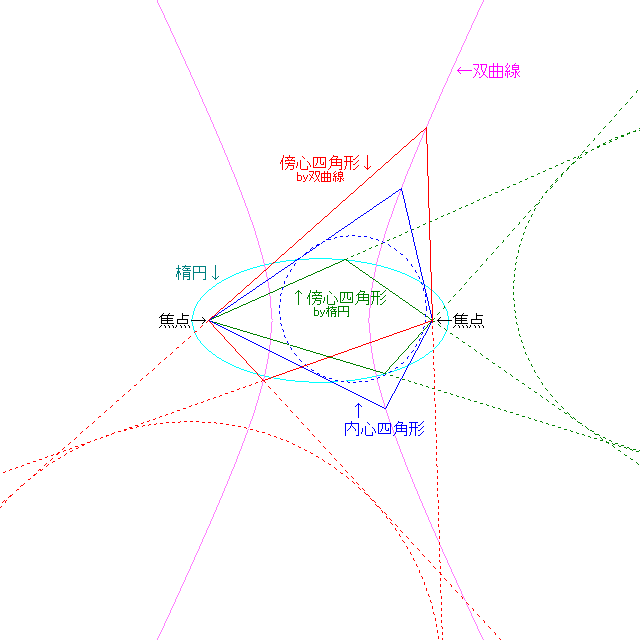
これは、楕円の2つの焦点と、楕円周上の2点を交互に結ぶ形となります。
そしてこれは、傍心四角形の式に一致することに気付きました。
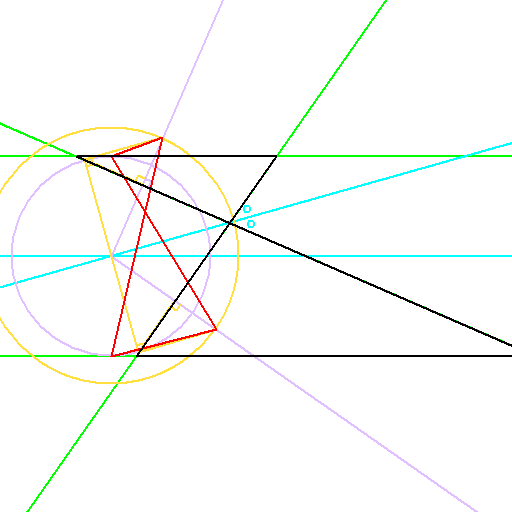
これにより逆に内心四角形も、双曲線を用いて以下のように表現できます。
ただ、台形と図の上で結びつく方法が見出せないのと、
傍心四角形は外心四角形(またはその延長線で表現できる無限遠の辺を持つ四角形)と
双対関係になってると解釈した方が自然そうなので、4つめの要素としては妥当ではないように思います。
式の形の類似性は、角度と長さはかなり異なる概念なので、たまたまなのではないかなと思います。
2025.5.11