双対図形 - 聖根のアジト
双対図形
聖根のアジト / 図形等 / 双対図形
図形には、長方形⇔菱形、立方体⇔正八面体といった双対関係があります。
しかしこの双対関係は、通常は限られた多角形や多胞体に対してのみ論じられ、一般的な図形に対して論じられることは稀なようです。
ここではその辺を大まかに紹介して行きます。
中点を連結する方法
内接円との接点/外接円との接線を用いる方法
特定の円に対して極と極線を交換する方法
双対曲線
他分野との関り
正式な双対図形とはちょっと違うものになりますが、
図形の双対の話に触れる上で最も解り易いのが、中点を結ぶ方法だと思います。
例えば多角形において、各辺の中点を結んで行くと、以下のようになります。
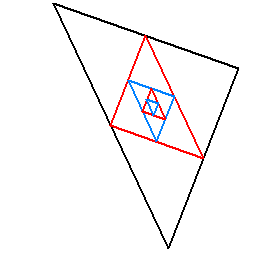

三角形なら、向きが反転しただけの相似な三角形が現れ、もう一度同じ操作を行うと、
元の三角形と同じ向きの相似な三角形が現れ、これが交互に無限に繰り返されています。
そして長方形の場合なら、菱形と長方形の無限の繰り返しとなっています。
多面体の場合は、各面の中点を結びます。
これにより、下図のように立方体⇔正八面体、正十二面体⇔正二十面体で交互に繰り返される形となります。
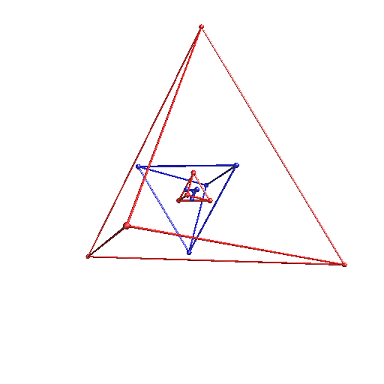
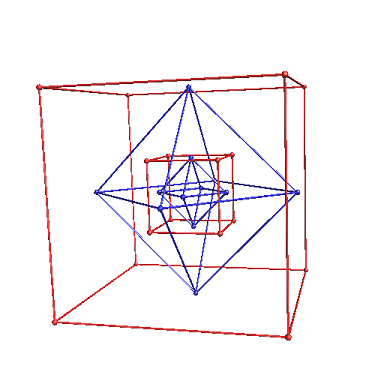
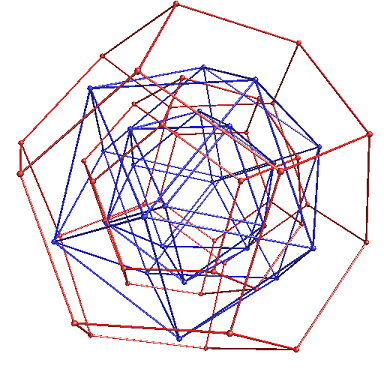
この時、辺の数は互いに等しく、面の数と頂点の数が入れ替わるという性質があります。
正式な双対図形とはちょっと違うとは書きましたが、
同じ操作の繰り返しで同じ図形が交互に現れる点から、これらも対関係の一種と見て良いと思います。
ただしこの方法は、極一部の多角形や多面体にしか通用しません。
例えば、特に特徴の無い四角形に対してこの操作を行うと、下図のようになります。
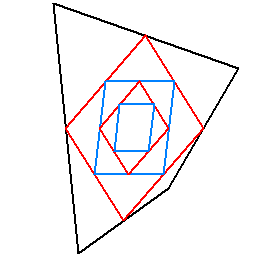
まず平行四辺形が現れ、後は異なる平行四辺形同士が交互に繰り返されています。
最初の四角形は、二度と現れません。
双対と言えるのは平行四辺形同士だけで、元の四角形の特徴は消えてしまいます。
多面体においては、例えば半正多面体に対してこれを行うと、各面が折れ曲がってしまいます。
折れ曲がる分面が増えるので、頂点の数⇔面の数という入れ替えも上手くいかなくなります。
前項に挙げた半正多面体にもちゃんと双対となる多面体は存在しており、それはカタランの立体と呼ばれています。
このカタランの立体は、半正多面体の外接球の各頂点における接面を結ぶことで作成できます。
これは二次元で例えると、以下のように円に内接する黒い四角形(外心四角形/円内接四角形/内接四角形)から、
外接する赤い四角形(内心四角形/円外接四角形/外接四角形)を作る方法に相当します。

この方法であれば以下のように、等脚台形と凧形の双対性も見えてきます。
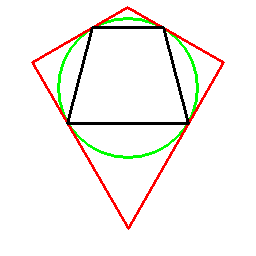
交差型の外接四角形に対しても、以下のように考えることができます。
場合によっては、内心四角形の代わりに傍心四角形(傍接四角形)が現れます
(頂点が無限遠点にある内心四角形も存在しているという見方もできるかもしれません)。
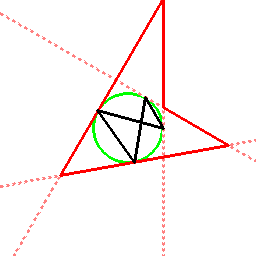
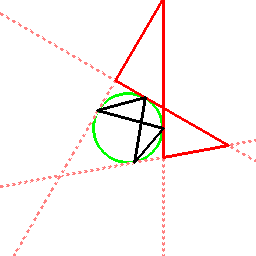
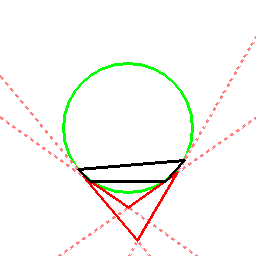
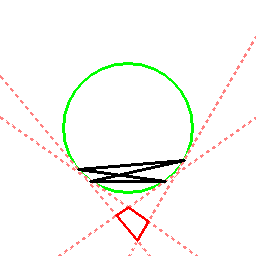
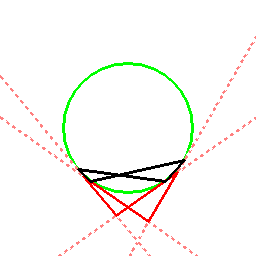
このように、内心四角形と外心四角形(または傍心四角形)は、一対一で結びつき、
一種の表裏一体の関係を成しています。
では、これが双対関係を表すものかということになりますが、この方法は当然ながら、
内心も外心も無い場合には定義できないのがまずネックです。
更に、「同じ操作で元に戻る」という条件を満たしていないと、双対と呼ぶには弱いのではないかと思います。
ここでは、「内接円との接点を結ぶ」という操作と、「外接円との接線を伸ばして結ぶ」という操作が同じと言えるのか、
確認する必要があります。
それには、内接円も外接円も持つケース(双心四角形)で試してみれば良いです。
そして下図のケースを見ると、内側の等脚台形と外側の等脚台形が相似ではないこと、
そして更にその外側は(有限の範囲では)四角形にすらなっておらず、
このことにより、両者は異なる操作であることがわかります。
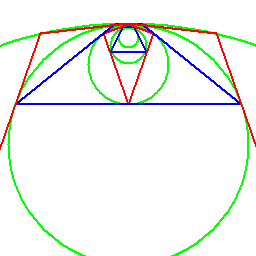
三角形は必ず内心も外心も持つので、そちらで試しても良いです。
前項では、「内接円との接点を結ぶ操作」と「外接円との接線を伸ばして結ぶ操作」は別物であるとなりましたが、
実は一概にそうとも言えません。
同じ円を基準に取れば、これらは同じ操作となって来ます。
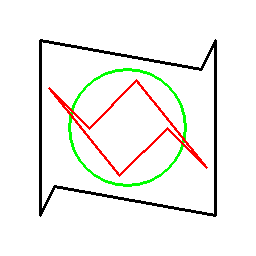
どちらも、特定の円に対して、極(点)と極線の交換というものを行う操作になっているのです。
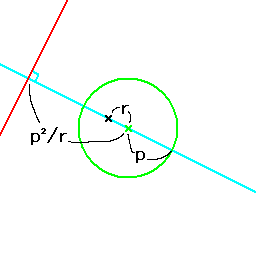
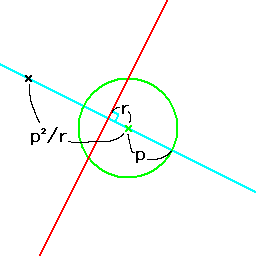
下図は極と極線の例で、黒い×印が極、赤い線がそれに対する極線となっています。
これらは、緑の円の中心との距離と円の半径の比が逆数となった関係となっています。
前項の双心四角形の場合は、内接円と外接円が別の円として存在しており、
前者の操作では内接円を、後者の操作では外接円を基準に用いたために、異なる結果となったというわけです。
一方、「内接円との接点を結ぶ操作」で作成した四角形における外接円と、元の四角形の内接円は同じ円です。
この場合、「元の四角形の内接円との接点を結ぶ操作」と、「作成した四角形の外接円との接線を伸ばして結ぶ操作」は同じものとなります。
つまり、「同じ操作で元に戻る」が成り立つと言えます。
この方法は更に、内心も外心も存在しない場合に対しても定義が可能です。
そしてあらゆる多角形に対し、以下のように双対関係を考えることができます。
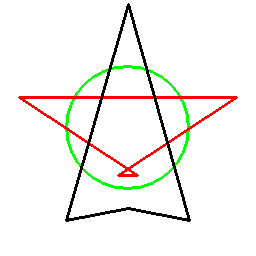
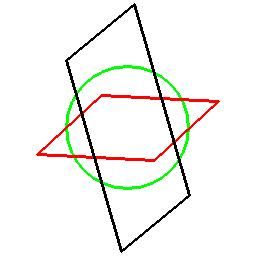
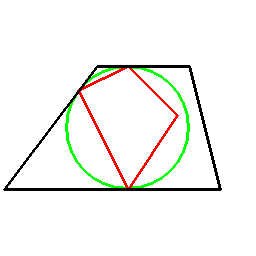
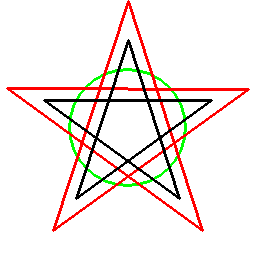
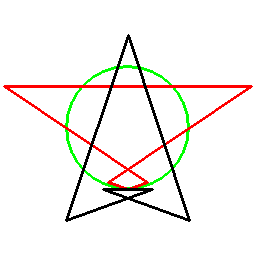
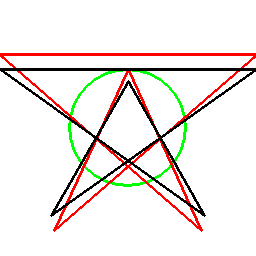
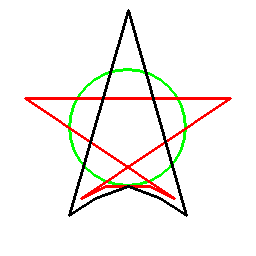
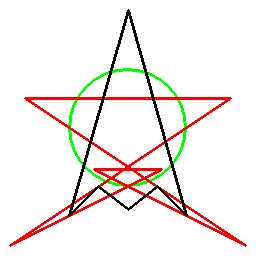
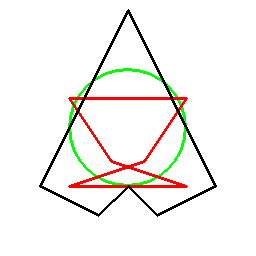
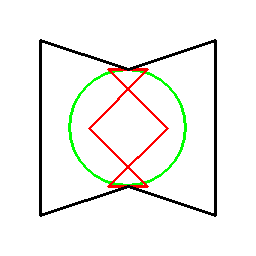
ただこの方法の場合、図形に対して一意には双対図形が決まらず、基準となる円を定義する必要があります。
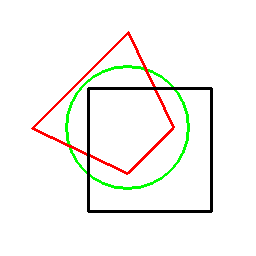
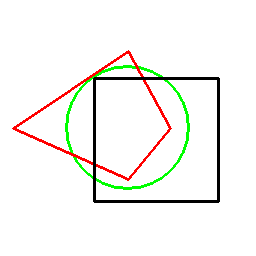
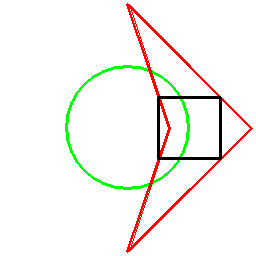
正方形の双対は通常は正方形ですが(自己双対)、この方法の場合、
基準となる円の取り方によって以下のように、様々な四角形が双対図形として現れます。

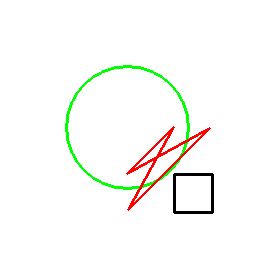
前項の考え方は、曲線に対してもそのまま応用でき、以下のようになります。
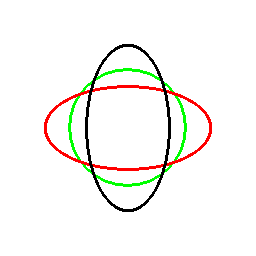
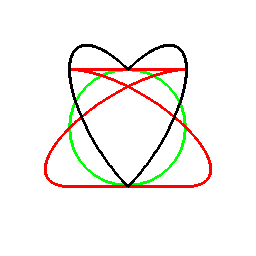
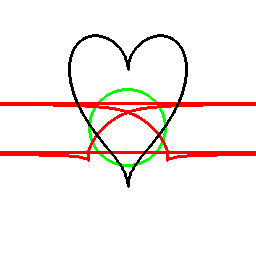
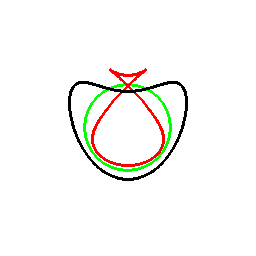
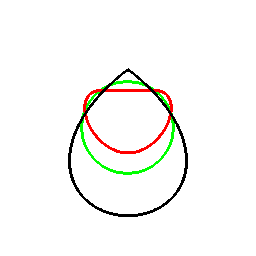
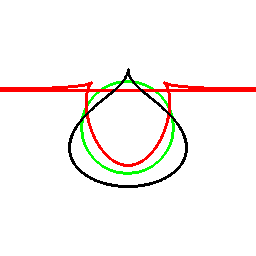
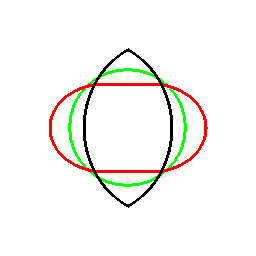
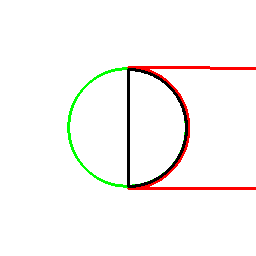
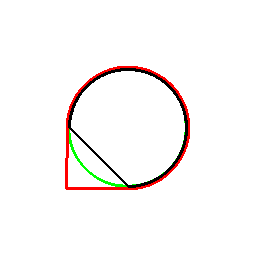
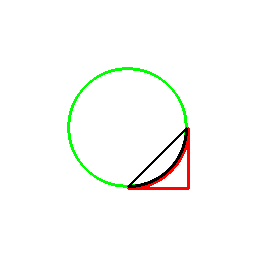
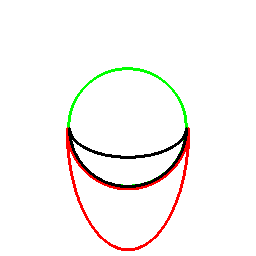
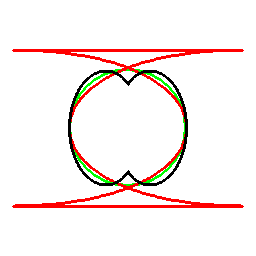
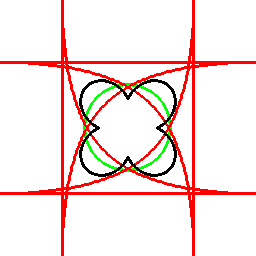
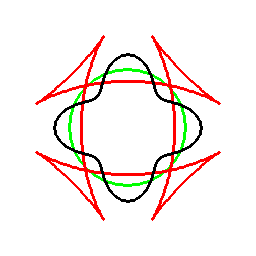
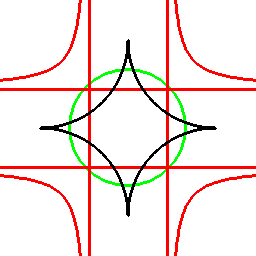
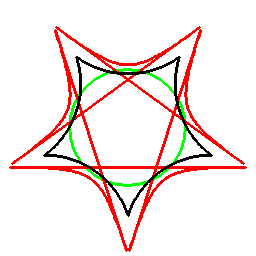
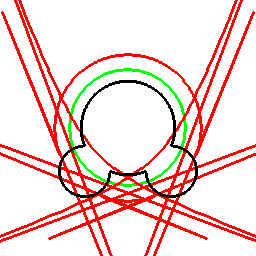
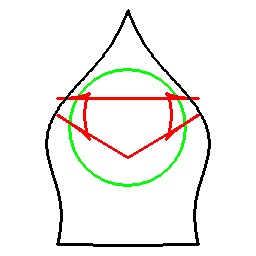
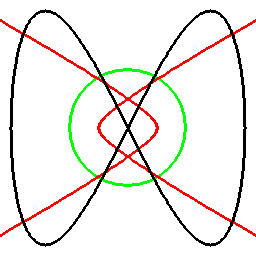
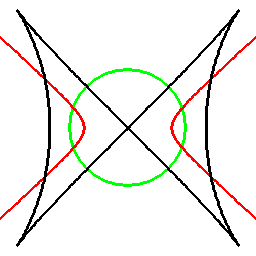
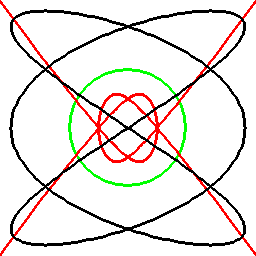
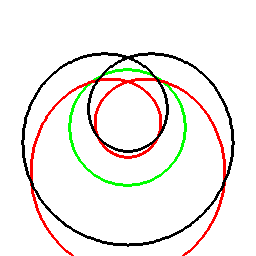
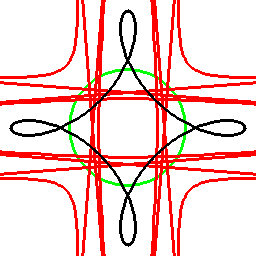
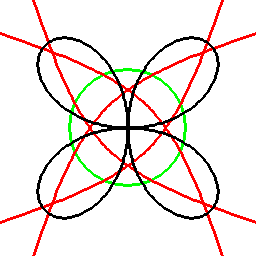

これは双対曲線と呼ばれるものと一致して来ます(正式な向きは逆かもしれません)。
接線が中心を通る箇所に対応する部分は、無限遠点へ発散しています。
式は、元の曲線をf(t)=(fx(t), fy(t))、基準の円の半径をpとすると、以下となります。
g(t)=(p2/(fxdfy/dt-fydfx/dt))(dfy/dt, -dfx/dt)
多面体の場合の双対関係と酷似したものに、グラフ理論と呼ばれるものの双対関係が存在します。
ただ、グラフ理論の場合は、角度や長さの概念はなく、「点が幾つあるか」「どの点とどの点が結びついているか」という情報のみがあります
例えば、下図の左右の図形は、グラフ理論上では同一のものです(こういう伸縮自在な性質は、トポロジーという分野で扱われています)。
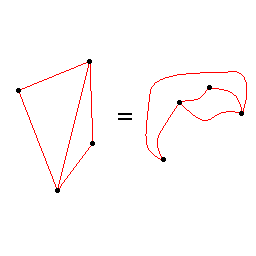
グラフ理論に角度や長さを加えて固くし、更にもう少しルールを加えたものが、多面体の世界という感じです。
このグラフ理論は、電気回路にも密接です。
電気回路の場合も角度や長さはありませんが、電源や抵抗、コンデンサといった素子により、
辺に個性が加わった形となっています。
この個性にも、抵抗⇔コンダクタンス、電圧源⇔電流源、コンデンサ(キャパシタンス)⇔コイル(インダクタンス)といった双対関係があるので、
併せて認識しておくと面白いかもしれません。
2025.5.4
図形等に戻る
トップに戻る

























































