(x,y,z)→(x,y)のような単純な投影です。
左側の図は、まず一番左上が正四面体に相当し、右へ行くと構成面となる正多角形の角の数が増えて行き、
下へ行くと一つの頂点に集まる面の数が増えて行く形になっています。
右側の図は、辺を幾つか追加したバージョンです。
聖根のアジト / 図形等 / 球面・双曲幾何関連 / 球面～双曲幾何上の平面充填の表現色々
正投影（正射投影）
ステレオ投影（平射投影／平射図法）
正距方位図法
心射投影（心射図法）
メルカトル図法
正距円筒図法
ランベルト正積円筒図法
心射円筒図法
(x,y,z)→(x,y)のような単純な投影です。
左側の図は、まず一番左上が正四面体に相当し、右へ行くと構成面となる正多角形の角の数が増えて行き、
下へ行くと一つの頂点に集まる面の数が増えて行く形になっています。
右側の図は、辺を幾つか追加したバージョンです。
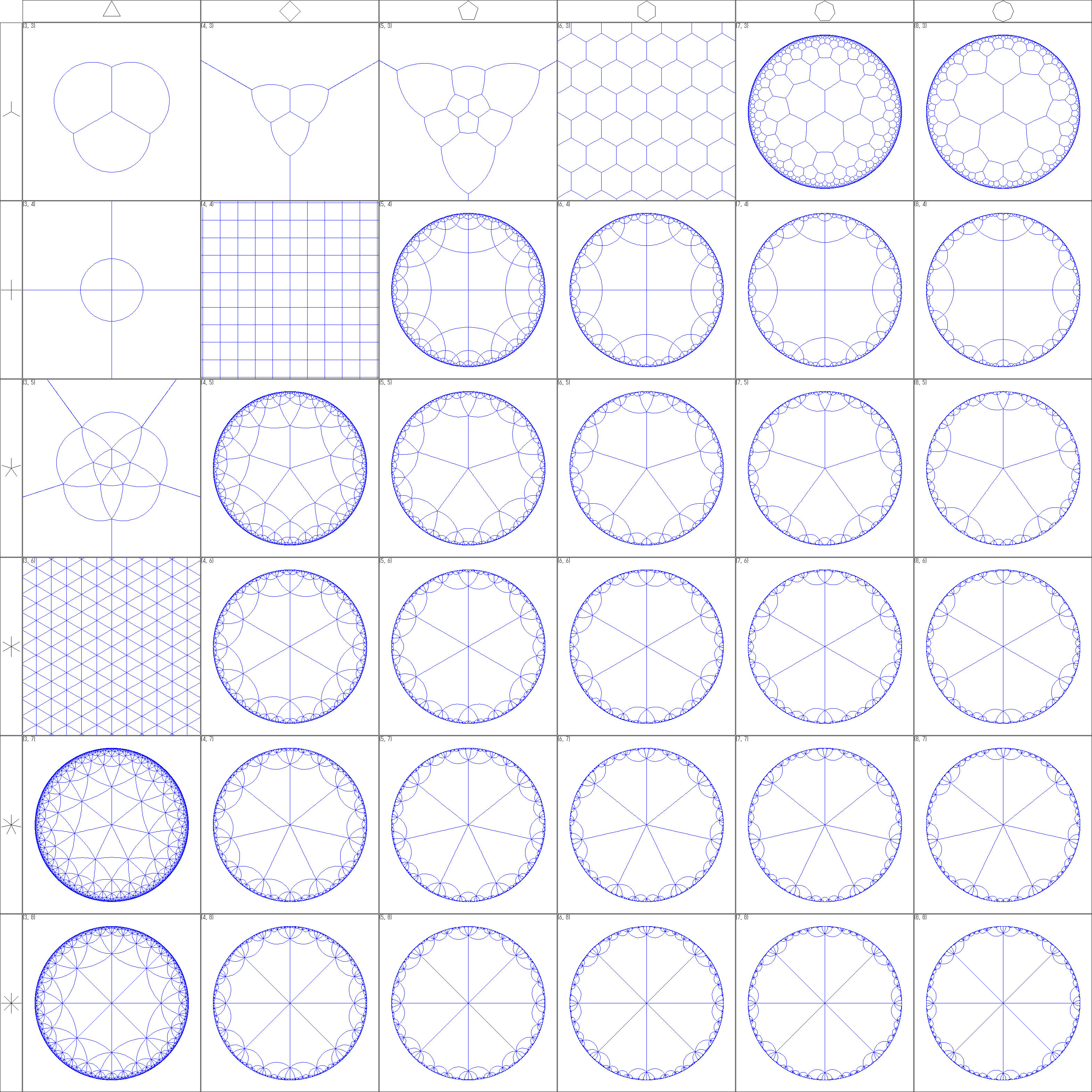
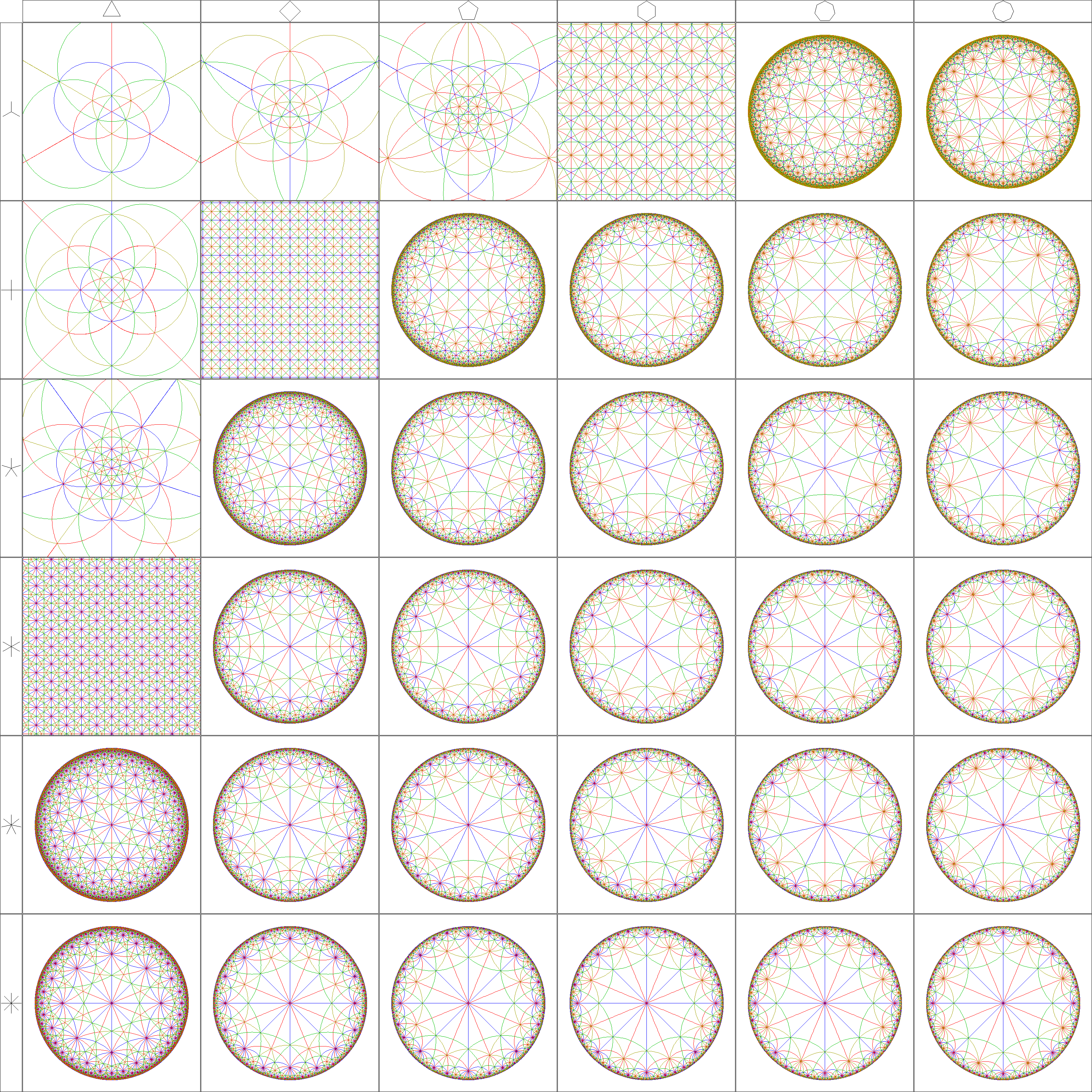
球面世界の場合、中心点の反対の点が無限遠点となります。
双曲世界の場合に同じ計算を行うと、お馴染みのポアンカレ円盤が出てきます。こちらは有限の範囲に収まります。
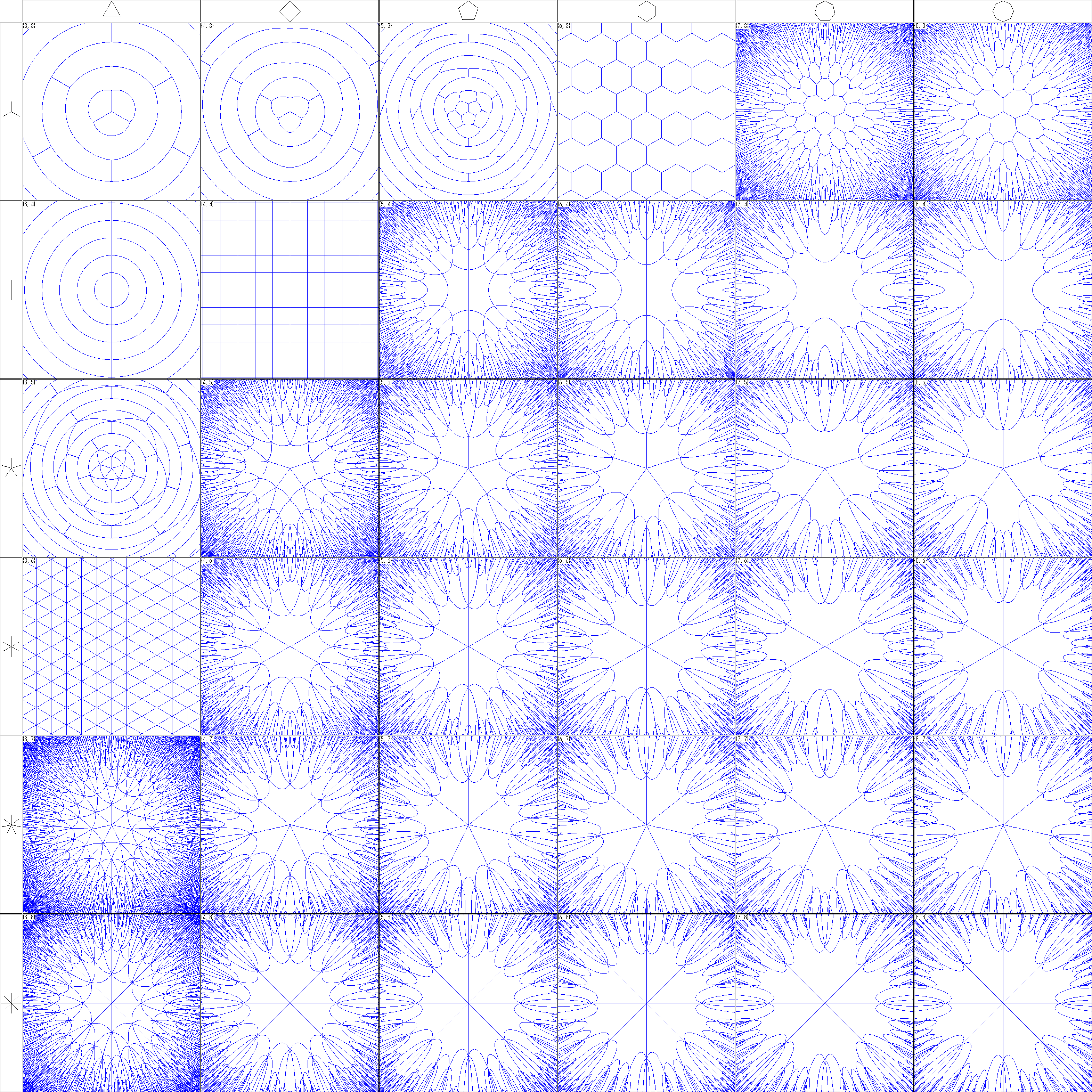
実際にこの世界に降りた時の視点に近いと思います。
球面世界なら、同じ景色が繰り返し見える形になっています。
投影結果も直線になります。
一般的な世界地図と同じ表現です。
経度をx軸、緯度をy軸にそのまま置き換えたようなものです。
正距円筒図法を筒状に丸めたまま正射影したようなものです。
メルカトル図法と似てますが別物です。
2023.10.13-2025.9.15