



平面の世界では、2角形を書こうとすると線分か平行線になってしまいますが、
球面の世界ではこのようにちゃんと描くことができます。
見る角度によっては、木の葉型、月型、ハート型が現れます。
聖根のアジト / 図形等 / 球面・双曲幾何関連 / 非ユークリッド幾何学上の一角形・二角形
digon on sphere




平面の世界では、2角形を書こうとすると線分か平行線になってしまいますが、
球面の世界ではこのようにちゃんと描くことができます。
見る角度によっては、木の葉型、月型、ハート型が現れます。

凹角を持つタイプです。

球面幾何学上の一角形が一角形として認められる場合に考えられるタイプの二角形です。
これは正二角形になるとは限りません。
解り辛いですが、二つ頂点があります。
monogon on sphere

球面幾何学上では一角形も可能ですが、いわゆる雫型にはならず、
このように角が180°に退化してしまい、零角形なんじゃないかと思える形になります。
monogon on cone
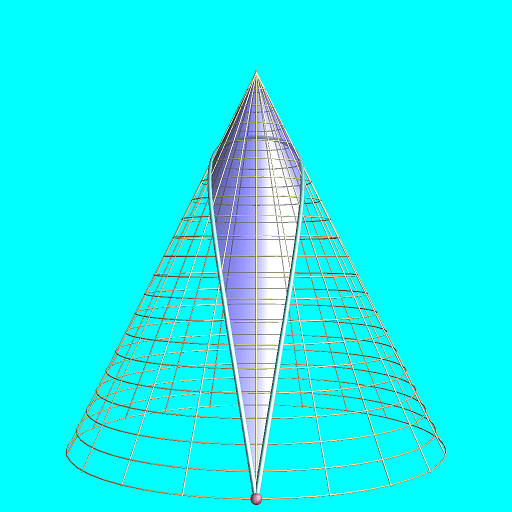





円錐面上ならば、ちゃんとした角を持つ一角形が実現できます。
円錐の角度によって、一角形の角度および形は一つに定まります。
ガウス曲率を持たない領域を通るだけで一角形を成している所がポイントのように思います。
円錐の頭頂点にあたる、曲率が無限大になる特異点的な領域を内部に持つのが注意点のように思いますが、
適当な球に置き換えればこの問題は回避できそうです。
monogon on sphere and cylinder






球と円柱を連結した図形の上でも、このようにちゃんとした角を持つ一角形が実現できます。
角度は0°~180°まで自由に取ることができます(凹角についても、円柱の反対側にも球をくっつけるか、
無限の面積を認めれば、取ることができます)。
2025.9.15