球面・双曲幾何関連

球面〜双曲幾何上の平面充填の表現色々
球面幾何学上の星型
基本情報
双曲幾何学と虚曲率

基本情報

球面幾何学

平面の世界では、2角形を書こうとすると線分になってしまいますが、
球面の世界では以下のようにちゃんと描くことができます。

このように、球面上の世界で繰り広げられる幾何学は、文字通り球面幾何学と呼ばれます。

球面幾何の世界では、大円（球を二等分するような円）が直線と見なされます。
三次元の世界で生きる我々にとっては、大円はあくまで曲線なのではないかとナンセンスに感じるかもしれませんが、
案外面白い性質があります。

四次元の超球の表面に拡張したものも考えることができ、その場合は二面体や三面体を考えることができます。
これに対し、通常の平面や空間の上での幾何学はユークリッド幾何学と呼ばれます。
そして球面幾何学は非ユークリッド幾何学の一種とされます。

なお一角形については、見た目が大円と同じになり、いわゆる180°以外の角を一つ持つ一角形を描くことは
球面幾何学の上でもできません。

楕円幾何学と双曲幾何学

球面幾何学は楕円幾何学の特殊な場合であり、更にそのペアとなるものに双曲幾何学があります。
これらも非ユークリッド幾何学の一種とされます。
これらの名前の由来はよくわかりませんが、とりあえず楕円体の表面は楕円幾何学の世界になりますし、
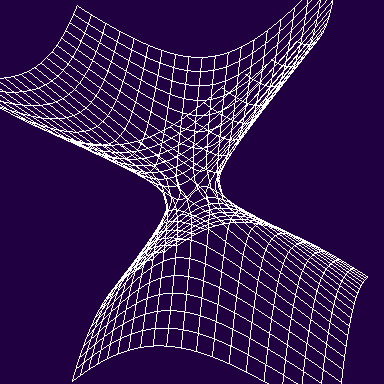
一葉双曲面は双曲幾何学の世界になります。
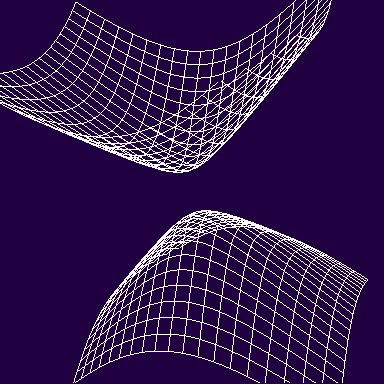
ただし、双曲面は双曲面でも、二葉双曲面の表面は楕円幾何学の世界なので注意です。

楕円体	一葉双曲面	二葉双曲面	鞍型

楕円幾何学なのか双曲幾何学なのかを判別する基準は、元々は平行線の性質によります。
ユークリッド幾何学上では、とある線に平行でとある点を通る直線が必ず一本だけ存在しますが、
これが一本も存在しないのが楕円幾何学であり、幾つも存在するのが双曲幾何学です。
楕円幾何学や双曲幾何学は、曲面上の幾何学を論じようとして生まれたわけではなく、
「平行線公準」なるものを証明するために、これを守らずに幾何学を組み立てて反証を得ようとした結果、
逆に新しい幾何学の体系として成立してしまったものらしいです。
どんな図形の表面にあたるのかは二の次で、その図形が上手く表現できない場合すらあります。

この平行線の性質は結局の所、ガウス曲率というものの正負によります。
ガウス曲率は大まかに言えば、縦の曲率と横の曲率の掛け算のようなものです。
もう少し正確には、最大の曲率と最小の曲率の掛け算のようです。
通常の曲率の場合、曲がる方向によって正負が反転しますが、ガウス曲率は凸面でも凹面でも正です。
一方、以下のような鞍のような形は、負のガウス曲率を持ちます。

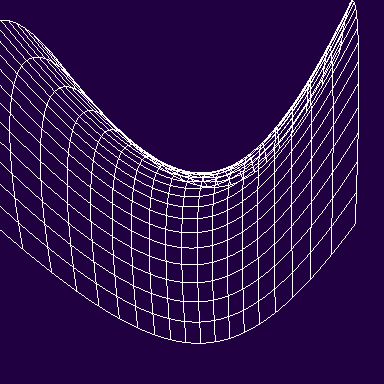
円柱や円錐を構成する曲面も曲面には違いなく、曲率もありますが、ガウス曲率は0です。
展開図の作れる曲面はガウス曲率0です。
球面幾何学は結局の所、ガウス曲率が至る所で正の一定値となる世界の幾何学ということとなります。

まとめると以下となります。

	楕円幾何学	ユークリッド幾何学	双曲幾何学
とある点を通りとある直線に平行な直線の数	0	1	∞
三角形の内角の和	180°超	180°	180°未満
ガウス曲率	正	0	負

楕円幾何学・双曲幾何学という呼称に対し、ユークリッド幾何学を放物幾何学と呼ぶこともあるらしいですが、
放物面は楕円幾何学の世界なので注意です。
どの辺が放物線なのかは謎ですが、放物線は、楕円と双曲線と共に円錐曲線と呼ばれ、色々な所で楕円と双曲線の中間に
現れることが関連しているのではないかと思います。

双曲幾何学の表現

ガウス曲率が正の一定値を取る場合が、球の表面で表現できるのに対し、
ガウス曲率が負の一定値を取る場合は難しいです。
上記の一葉双曲面や鞍型は、ガウス曲率が常に負とはなりますが、一定ではありません。

ガウス曲率が負の一定値を取る図形としては、以下のベルトラミーの擬球が存在します。

しかしこの図形は、ラッパ同士が繋がってる部分については曲率が発散してしまうので、
双曲幾何学の世界を完全に表すことはできません。

双曲幾何学の世界を表現するには、ポワンカレの上半平面モデルと
ポワンカレの円板モデルがよく用いられます。

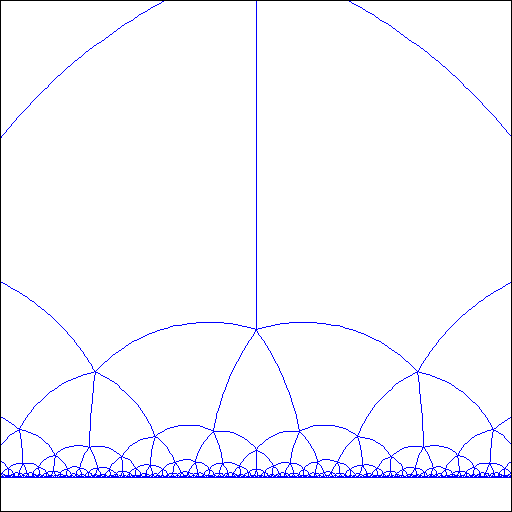
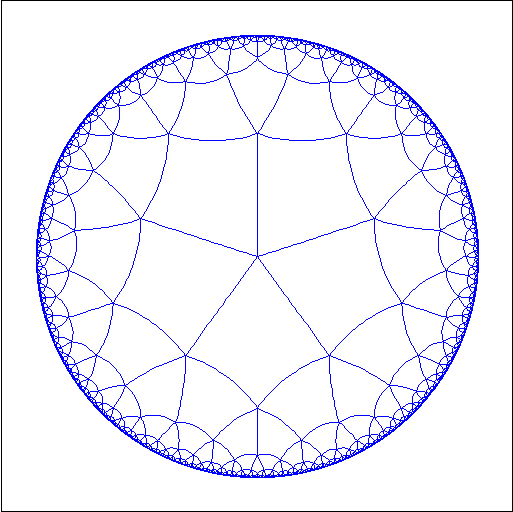
これらは辺の長さは見た目通りではないので注意です。
上図の場合、合同な正方形で埋め尽くしている様子となっています。

楕円・双曲幾何学における平面充填

実際の図はこちらでまとめてますが、
平面を一種類で埋め尽くすことのできる正多角形は、正三角形と正方形と正六角形の3種のみです。
この時、各頂点に集まる正多角形の数は、それぞれ6つ、4つ、3つで限定となっています。
これに対し、楕円・双曲幾何学を合わせると、あらゆる正多角形で平面充填が可能であり、 各頂点に集まる正多角形の数も自由となります。
球面幾何学における平面充填の条件は、正多面体の条件と同じであり、
正多面体を球面に投射したものがそのまま、球面幾何学における平面充填の様子となります。

2025.2.12-15

双曲幾何学と虚曲率

上述のように、ガウス曲率が正で一定の場合が球面上で表現できるのに対し、
ガウス曲率が負で一定の場合は同様の表現が困難であることを長年奇怪に思っています。
ベルトラミーの擬球は、完全には双曲幾何学の世界を表すことはできないことに加え、
ガウス曲率は一定でも通常の曲率は一定ではないことや、
円柱のようにループしている所も気になる所です。

これに対して、異端論かもしれませんが、虚数の曲率を考えることですっきりまとまります。

まず、ガウス曲率の定義に立ち返ってみます。
ガウス曲率が負であるということは、方向によって曲率がプラスになったりマイナスになったりと
変動するということなので、その時点で、どの方向に対しても曲率が一定である球と同じようには行きません。
しかしそれはあくまで曲率を実数に制限した場合の話です。
虚数の曲率を認めれば、どの方向にも一定であり、なおかつガウス曲率がマイナスとなる状態が可能となります。

では、曲率が虚数であるとはどういう状態なのか。
曲率aが円の式は、
x²+y²=(1/a)²
となるため、これがこのまま当て嵌まると仮定すると、曲率がaiの場合は
x²+y²=(1/(ai))²=-(1/a)²
という、半径が純虚数の円の式となります。

しかし、円では結局の所、三次元にしても球面幾何学となってしまいそうです。
ただ、円の式というものは、双曲線の式と表裏一体です。
先程の式も、
x²-(iy)²=(1/(ai))²=-(1/a)²
のように変形すると、xとyの片方が実数で片方が純虚数の双曲線も表していることがわかります。
双曲線なら無限に伸びるので使えそうです。

これについて、別のアプローチにより確認します。
まず、原点を通る曲率aの軌跡上の点は、以下の式となります。
(1/a)(sin(at),cos(at)-1)
このaを純虚数とし、a→ibと置き換えると
(1/ib)(sin(ibt),cos(ibt)-1)=(1/b)(sinh(bt),-icosh(bt)+i)　…　�@
となり、やはり片方が実数で片方が純虚数の双曲線の軌跡を成すものとなります。
先程の虚数の円は、虚数方向に伸びている直線が虚数の曲率を持った結果であり、
対してこちらは、実数方向に伸びている直線が虚数の曲率の持った結果と言えると思います。

しかし、双曲線は曲率一定ではありません。
ここで、距離についてちょっと特殊な解釈をします。
通常は、ベクトルの要素が複素数である場合、例えば(a+bi,c+di)と(0,0)との間の距離は、
√((a+bi)(a+bi)^*+(c+di)(c+di)^*)=√(a²+b²+c²+d²)
と定義されてたと思いますが、これを純粋にピタゴラスの定理を当てはめて
√((a+bi)²+(c+di)²)として考えます。
すると、(a,0)と(0,ai)との間の距離が0となって気持ち悪いかもしれませんが、
そういう特殊な距離だと割り切って、ひとまず目をつむります。
そうなると下図のように、グラフ表現の上での長さは違えども、実際の長さは等しいという形となります。

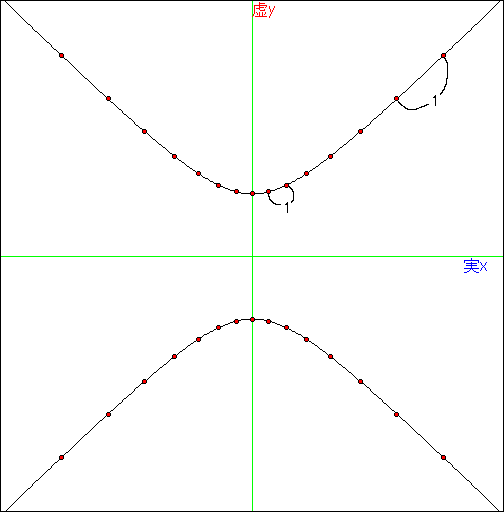
この考え方に基づけば、この双曲線は曲率一定となって来ます。

そして、球面幾何学の世界が、三次元空間では(x,y,±√(1-x²-y²))のように表現されるのに対し、
ガウス曲率が負で一定の世界は(x,y,±i√(1+x²+y²))のように表現される事となります。
これは結局、xy成分が実数でz成分が純虚数の二葉双曲面となり、
これこそが双曲幾何学の世界を現す真の図形と考えることができるのではないかと思います。

そしてこの方法に基づいた双曲面に対して、球面幾何学いおけるステレオ投影（平射図法？）と同じ計算を行うと、
ポワンカレの円板モデルらしきものができあがります。
ポワンカレの円板モデルは結局の所、ステレオ投影と本質的に等価であると言えるのではないかと思います。

2023.9.22-2025.2.15

図形等に戻る
トップに戻る