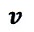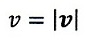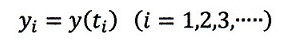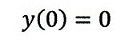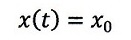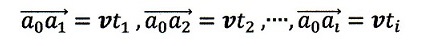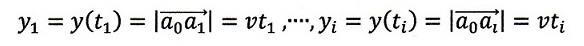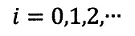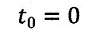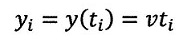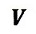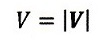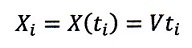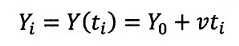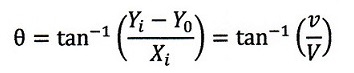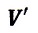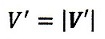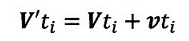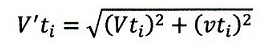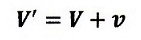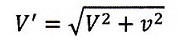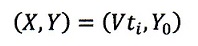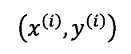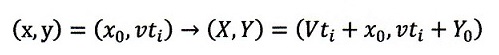座標変換と物理についての疑問(独断私見)
最近一旦削除してしまいましたが、あるサイト記事を目にしたとき、最初はその方の主張
がわからず、考えているうちにはたと理解したというか気がついたことがあって、それを
相対性理論への疑念の一項目で長くUPしてました(元の参考にした個人サイトは、それ
についての分をなぜか抹消されてしまいましたので紹介できませんm(__)m)
ただ、折角自分で思いついた私見でしたので、再度全面改定の上、単独articleとするこ
とにしました。
タイトルの「座標変換」というのは「『運動系』
の中の物体の運動を『静止系』に座
標変換する」という話です。ときに人はこれを「静止系から見たら」と表現します。
尚、ここで、取り上げようとしているのは、「『運動系』内でその系全体が『静止系』に
対して運動している方向と直角方向であるとき」を対象とします。
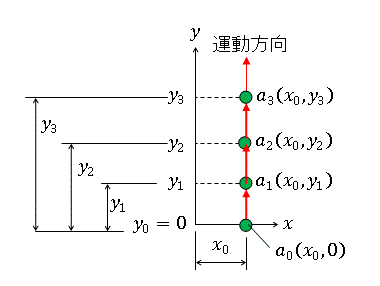
運動系内におけるこの物体を運動を運動系座標系で表したものを図1に示します。
 |
|
図1 運動系内の運動
|
運動系全体が静止系に対して等速運動している方向にx軸をとり、これと直角方向にy軸
をとることにします。そして、運動系内で物体aがy軸に平行方向にy軸の正の方向に等速
直線運動しているとします。物体の運動系に対する速度(ベクトル)、速さ(スカラ)を
|
速度: | 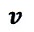 |
|
速さ: | 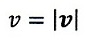
|
とします。尚、本項では、
速度:大きさと方向を持つベクトル値(ボールド体で示します)
速さ:大きさだけのスカラー値
と厳密に区別します。
また、図のi番目の位置の時間tiに対するy軸座標値を
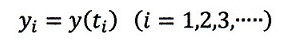 | ・・・(1)
|
とし、t=0で、
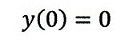 | ・・・(2)
|
とします。また、x軸座標は全ての時間tに対し、
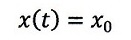 | ・・・(3)
|
とします。このとき、
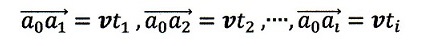 | ・・・(4)
|
であり、
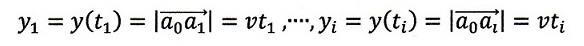 | ・・・(5)
|
となります。ここで、
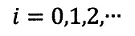 | ・・・(6)
|
と拡張し、
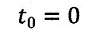 | ・・・(7)
|
とおきますと、(5)は一般に、
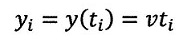 | ・・・(8)
|
となります。今、この運動座標系(x、y)の原点に観測者"o"がいてこの物体の運動を観
測しているとしますと、物体はx軸位置が(3)で、yの正の方向に、t=0でy=0から、各時
間のy軸方向位置が(6)となるように観測するはずです。
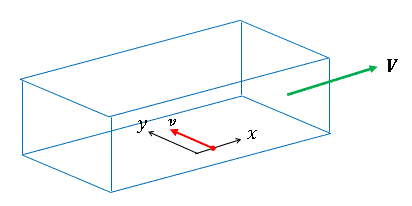
さて、この(x,y)座標系が例えば、図2のように電車の中にその原点が固定されて、図の
ように設置し、その原点に観測者がいるとします。もし、この電車が透明で中が外から見
えるとしましょう。
 |
|
図2 運動系の例
|
この透明電車は等速運動しているとし、静止系に対する速度(ベクトル)、速さ(スカラ)を
|
速度: | 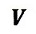 |
|
速さ: | 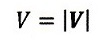
|
とします。そして、静止系に透明電車の進行方向にX軸の正の方向を取り、これと直角で
電車の幅方向にY軸を取り、その原点に静止系の観測者がいるとします。したがって、
X//x、Y//yとなります。また、t=0でY軸とy軸が一致するようにしておきます。
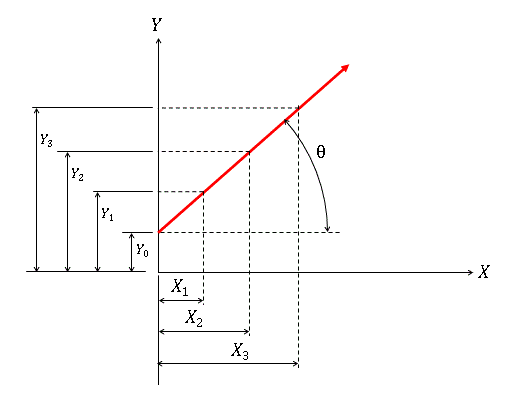
このとき、普通は、最初から「静止系から見た運動系内の物体aの運動」として図3をただ
ちに描くのではないでしょうか?
 |
|
図3 静止系から見て
|
(6)、(7)としますと、
となります。そして、速度(ベクトル)と速さ(スカラ)を
|
速度: | 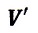 |
|
速さ: | 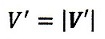
|
としますと、時間tiのときの赤斜線のt=0からの距離は
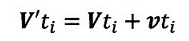 | ・・・(12) (ベクトル) |
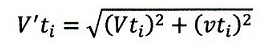 | ・・・(13) (スカラ)
|
となりますので、
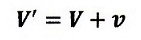 | ・・・(12) (速度/ベクトル) |
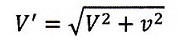 | ・・・(13) (速さ/スカラ)
|
となります。
(12)式を「速度の合成」と称しています。「静止系から見ると透明電車内の物体は
この速度で赤斜線方向に進む」というわけです。
速度に関する「ガリレイ変換」ですね。V’は「相対速度」となるわけです。
普通はこれで終わりですが、一つ、すごく基本的な疑問が湧いて来てしまいました。
それは、これは次のどちらなのかということです。
(a)合成速度V’で実際に赤斜線方向に進んでいる
(b)「静止系から見ると」合成速度(相対速度)V’で赤斜線方向に
進んでいるように見える
私は(b)だと思っているのですが。で、もし(a)なら運動系内の運動は何なんでしょうか?
(a1)実際は静止系が実運動で運動系内は単に相対的な運動
(a2)どちらも実運動
のいずれなのか?という疑問です。
で、これはどうでしょうか?
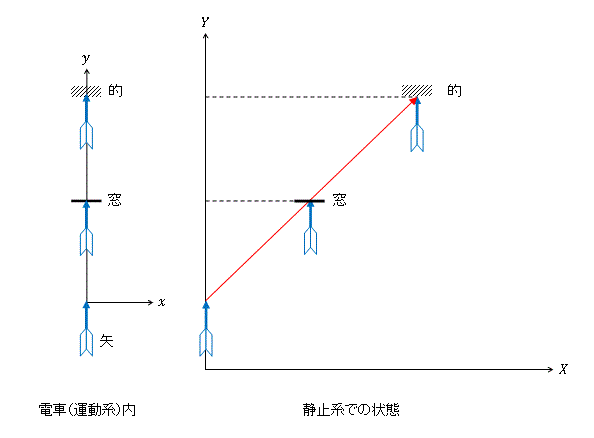
空気抵抗・風・重力を無視したとき、電車内の観察者がy軸方向に矢を放ったとします。
丁度、電車の窓があいていて外に飛び出したとします。電車内観測者から見ればその
まま真っ直ぐに飛んで行っていつも矢の尻を見ていてどんどんそのまま小さくなっていく
はずです。で、偶然、的があってそれに当ったのを見たとします。
これを「静止系から見たら」どうなるでしょうか?図4ですよね?
 |
|
図4
|
「ガリレイの相対性原理」というのは「質点の運動」に関するものです。
そしてそれは、結局は、「全ての系において距離・時間の尺度が一定」ということを
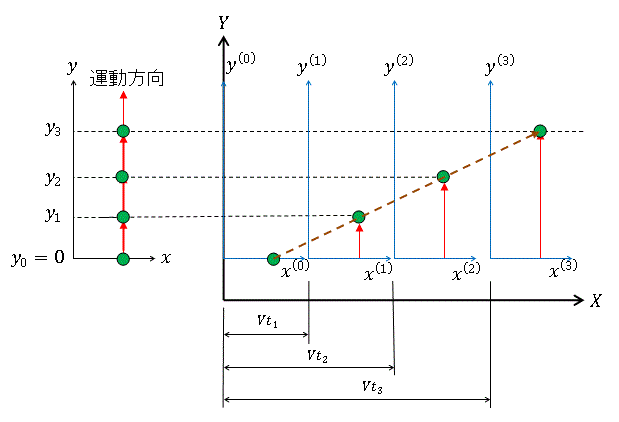
前提とした「数学的一次座標変換」なのです。図で示します。
 |
|
図5
|
図5に示すように、時間tiのとき、
に原点を置く
座標系が静止座標系(X,Y)に投影されたものです。すなわち物体と座標軸が(X,Y)に投影
され、時間tiに置ける物体の位置は
と「一次座標変換」されるのです。
そうなるとどうなるでしょうか?各時間の物体位置を結ぶ線が斜線ということになります。
図の赤矢印線は運動系内のその時間までの物体の軌跡となり、その方向は速度ベクトルv
の方向と一致しています。
結局、斜線は「各時間の物体位置を結んだ仮想線」となるのです。
すなわち、単に幾何学的な関係からそうなるにすぎず、
「静止系から見たら」斜線のような行程に見えるだけ
にすぎないというのが私の解釈です。
(’14/4)
目次に戻る