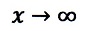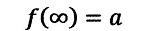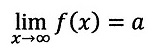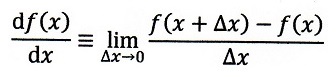科学における無限について②
前項で述べた、『数学』という学問世界の情況に鑑みれば、必然的
に、
数学を無条件・無制限に現実世界である
『自然科学』に適用してはならない
ということは明白でしょう。しかしながら、結構、混同しているような
向きが見られてなりません。これは、私だけの勝手な思い込みかも
しれませんが・・・
さて、前項で示した数学における「実無限」ですが、「無限に数え終
えた」という「神の視点」のものでしたから、「現実世界」では考えに
くいですよね?「数学」で考えてしまうのは、もうそこには「自然で素
朴な見方」というのから離れてしまっていて、『自然』ではないと考え
てください。あくまで、万人に共通な「自然で素朴な見方」という意味
での話です。
本来、「現実世界」を扱う『自然科学』は「自然で素朴な見方」が根源
にあらねばならないと考えますので、『自然科学』での無限は、我々
の直観通り、本質的には「可能無限」ではないかと思うのです。
また、『数学』の世界では、「その値が無限に大きくなる」無限大
と「その値が無限に小さくなる」無限小があります。したがって、
『数学』の世界では、『実無限』としての無限大、無限小、『可能無限』
としての無限大、無限小が概念として存在しています。しかしながら、
現実世界を扱う『自然科学』の世界に存在するのは『可能無限』の
うちの無限大のみではないでしょうか?(勿論、現実世界に無限大
があるかという議論はあるとは思いますが、結論が出ているわけで
はありません)
「ゼノンの逆理」というのを考えてみましょう。これは現実世界の話を
数学世界で考えようとしたために出てきたパラドックスだと思うので
す。私がここで云う「数学世界」というのは、『点』という概念です。
『点』というのは、数学世界で「面積がない」ものとして定義されたも
のです。ですから、本質的に見て、そういう点をどれだけ並べても
『線』にはならないということがこの『パラドックス』をパラドックスとし
ている所以ではないでしょうか?結局、数学世界では、『可能無限』
での『無限小』では現実世界との矛盾が出てしまっただけであり、
『点』『直線』の定義をそのままにして、現実世界と突き合わせるた
めに「実無限」での『無限小』という概念を導入せざるを得なかった
のではないでしょうか?
しかしながら、現実世界ではどうでしょうか?「面積がない」点など
というのは現実世界にはありません。最小でも必ず「有限値」なの
です。「無限分割」というのは「数学」の世界だけの話なのです。
すなわち、
(直線)=(最小有限長さ)×(有限個)
なのです。その意味で、本質的には現実世界には無限小と言うの
は存在しないのです(恐らく、こんなことは多くの科学者はわざわ
ざ言わないだけで、御承知のことと思いますが、ネット見ていると、
どうも数学と自然科学である物理学を混同しているとしか思えない
方が見られますので、私自身の中での論理的結論としてここに示
しました)。
さて、
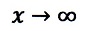
のとき、すなわち、xの値を無限に大きくしていく時、xの関数f(x)を
を考えます。このとき、
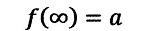
とするのは実無限で無限を定義する数学の世界では問題ない表
現と思いますが、自然科学である物理学の世界では概念的に間
違いであり、自然科学では本来の定義通り、
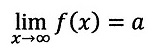
ではないでしょうか?前述のように∞というのは単なる記号でし
かなく、現実には存在しない数値だからです。
そして、この式の右辺aは、この値に限りなく近づいて行くという
極限の予想値であり、どこまで行っても常に近似値なのです。
前述のように、本質的には現実世界は「可能無限」の世界だから
です。
ところで、微分・積分というのが物理の世界では多用されていま
す。これは、物理理論を表すのに数式が必須であるのと、理想的
基本的な概念として理論を構成する必要上、物理学を数学に還
元したのが最初でしょう。
本質的には、物理学は現実世界の『自然科学』ですので、前述の
ように『無限小』というのはないはずですが、数学に還元したゆえ
に、数学世界での『無限小』の概念が使われているのです。
私はそこを強調しておきたいのです。
微小長さΔxは数値があって、有限長として実在していますが、
究極を表すdxは、そもそもは
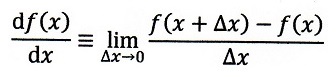
で定義された、いわばシンボルでしかなく実体はないのです。
我々はこの「dx」というシンボルを「限りなく0に近いΔxの極限値」
というような説明で納得した気になっていますが、よ~く考えてみ
れば、そんなものは自然にはありません。
有限な最小のΔxの代わりに予想近似値として使っているだけと
言うのが真実ではないでしょうか?
尚、誤解の無いように言っておきますが、私はそれを使用するの
がおかしいなどと言っているわけではなく、きちんと実体を認識
した上で使用すべきと主張しているだけです。そうでないと、数学
が独り歩きしてしまうのです。実際、現状を見ますと、どうもそう
いう雰囲気になっている気が強くしています。
私がここで強調したかったことは、物理理論は数学の結論である
数式を使ってはいるが、数学における概念・言葉をそのまま自然
科学である物理学に適用して使うのは注意が必要であるというこ
とです。特に、無限に係わるものは留意が必要だということです。
目次に戻る