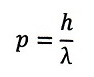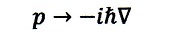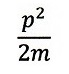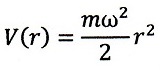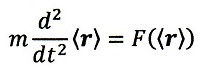「量子」について(5)
9/1までに例の「量子力学」の教科書、第四章「中心力場内の粒子」まで
読み終えました。ここまで読んで、シュレディンガー方程式がどういう道
程で導かれたか、色々な例でどのようにこの2次偏微分方程式を解くの
か等、触りについては理解できたつもりです。あくまで、「つもり」で応用
とまではいきませんが、こちとら、専門家では無く、単に趣味の世界で
やってるだけすので、根本的なところを詳細に確認したいという意図だ
けですから・・・(^_^;)。
ま、先にベクトル解析を多用した電磁気学の古い教科書を再勉強してき
ましたので、この教科書に出てくるグリーンの定理とかルジャンドル関数
とかベッセル関数とか変数分離法とかいうのは概略はわかっているつも
りでしたので、出てきましたが驚いたりせずに読み進められてます。
結論しか書かれていない数式は文章を繰り返し読み、理解しながら一つ
一つ自分で解いてPC文書でメモしています。
この本、隅々までどうやら冗長的な無駄な記述はなく全部が理解に必要
な感がしてますので、私の常の飛ばし読みは自分自身に厳禁にしている
ところです。
さて、表題には「一つの粒子の波動関数」とか「中心力場内の粒子とか」
いうように『粒子』という用語が出てくるのが私的には気にはなるのです
が、実際の式を見てますと、古典力学で『運動量保存の法則』として重要
な運動量pは
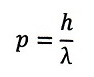
という波長と運動量の間の関係式がベースになって導出されている
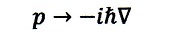
と演算子に置換されており、古典的「粒子」というもので出てくるパラメー
タは、運動エネルギー
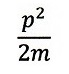
と、例えば調和振動子でのポテンシャルエネルギー
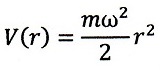
で出てくる『質量m』だけですよね。
で、この『質量m』というものですけど、電子などの粒子においては直接、
秤で測れるものではなく、逆算で求めているだけのものですから、言うな
れば『質量』という名前で呼んでいる一個のパラメータということです。
そして、先の方の項で述べたように、「自由粒子」を考えた時、波束の重
心位置rの期待値を<r>とすると、
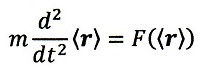
となって、巨視的な古典力学と一致するわけです。
ちなみに、「近似的」と言っている人がいますが、この式は決して近似式
ではなく、きちんと数学的に導出でき、物理的に意義もある量子力学と
古典力学の言わば「接点」なんですね。
元々、古典力学で『質量』というのは力を加速度で除したものをそう定義
しただけのパラメータというわけです。私は「存在が発見された」と喧伝
されている「ヒッグス粒子」なるものは未だ信じていません。例によって
「定説標準理論」というパラダイムにしたがって、つじつま合わせして、
再現実験もないまま「発見できた」と喧伝しているだけだって気がしてな
らないからです(実験に莫大な資金を投入していますから、そういうこと
もあるのではないかと思いますけどね)。不都合な「発見」は測定ミスだ
とか統計ミスだとか徹底的にけちつけてとしてうやむやにしてしまってい
ます(例の超光速ニュートリノ等)から余計そういう不信感が私にありま
す。
ネット見ていたら、情報源が不明ですけど、
「電子は、点であるが、ψという場に従う」
などと説明している先生がいるらしいですが、やっぱり、巨視的世界での
人間の「感覚」としての「もの」である「粒子」から離れられない人がアカデ
ミー科学界にもいるんですねぇ。ですから、一般下々がそう考えるのもや
むおえないのかもしれませんね。
結局、「『理論』はわかった」というだけで、未だ、「量子力学」の心髄を理
解・説明できていないというのが実態ではないかと思いますね。
いずれにしろ、「粒子を『波動』とするとどうなるか」という思考から、基本と
なるシュレディンガー方程式が導出されており、そこには論理的矛盾仮定
は一切入っていませんし、実証観測結果をきちんと説明できて工学応用
までされていることは重要なポイントです。
現在の科学には誤解を受けない最適な用語がない気がしますが、既存の
用語を使うなら、いかにも「もの」を表す「粒子」でなく、「波束」と言う方がよ
り実質に合致している気がします。これなら、「1個、2個」というような数え
方してもそうおかしくないでしょう。ま、今の解釈である「確率波の波束」っ
てなんなの?という疑問も出てくるでしょうが・・・
目次に戻る
次へ