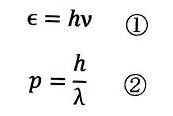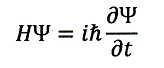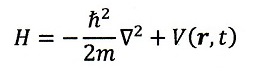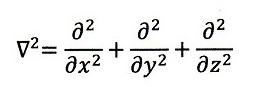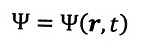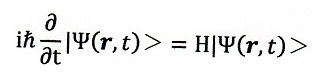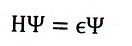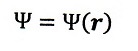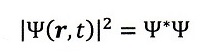「量子」について(1)
ずっと「量子」という用語の概念の混乱が気になっています。
人によって「粒子でも波でもない」とか、「粒子であって波である」とか説明
が異なっており、実に曖昧な定義のままで放置されている感がしていま
す。結局のところ、「『量子』とは何か」が曖昧のままでも理論が現象に完全
に一致しているからそれでいいだろうとなっている気がします。現に、ネット
にはそう書いている方もおられます(どういう属性の方かわかりませんので、
それが大多数の科学者の意識かどうかは不明ですが)。
それでも、恐らくは「『合理的・論理的』であること」を価値判断にされている
だろう「科学好き」な理系の方々は本音のところではなかなか納得・満足さ
れてはいないだろうと思います。
ま、しかし、科学者は曖昧なところで口を濁していますけど、科学者を含む
多くの人は、実際には
量子=波動の性質を持つ粒子
くらいに考えているのではないかと思います。実際、ネット見てましたら、や
はり、その通り「波動の性質を持つ粒子」だと主張している人がいました。
また、折角、ミクロの世界のものを「量子(quantum)」という概念を与えたの
に、構成している「もの」に対して「素粒子(elementaly particle)」という名称
を用いていることからも、科学者は「量子」というものを実際にはどういう風
に捉えているかは明確ですよね。結局のところ、どうしても「粒子」という
「物」からは離れられないんですね。
だから「電子」でも、教科書・啓蒙書に限らず、「球形」のモデルで説明して
いますから、それを読んで学ぶ側はどうしてもそういう「球形」のモデルのよ
うな存在のものと意識がすりこまれてしまっているわけです。
しかし、こういう地球人類の概念って「ほんとう」なんでしょうか?
実際、電子でも沢山「発見されている」素粒子と言われるものの姿・形とい
うのを可視できているわけではありません。素粒子はウイルソンの霧箱観
察写真で説明されますが、あれは言わば「軌跡」を捉えているにすぎませ
ん。
結局のところ、マクロ世界の「物」が砕かれると「粒」「粉」になることからの
「類推」で更に細かくしたものも「物」だと「思い込んでいる」だけではないで
しょうか?要するに、「証拠がどうの」という以前に、自然な常識的な考えか
ら「物」としての「粒子」という存在を「信じて」いるわけです。
ところが、実験観測結果が、ミクロ世界の「粒子」がマクロ世界の「波」にし
かない性質を有していることを示してしまったために、科学者は頭をかかえ
てしまったと言う訳です。
幸い、すでに当時、それを「解決」するような科学的情勢がありました。
溶鉱炉の温度をいかに特定するかという課題があり、実験がなされたので
すが、それまで常識となっていた知識(エネルギーが連続的である)では説
明できない結果があり、それを説明するため、「エネルギーは飛びとびの値
をとる」として、「エネルギー量子」という概念が導出されました。話によれば
発案したプランク自身はなかなか自分ではその結果を信じられなかったよう
です。ですから、本来、「量子」という概念はこの「エネルギー量子」によるも
のなんですね。そして、光電効果などの実験から、Einsteinが「光量子」とい
う概念を創出してました。波であると考えられてきた光に粒子の性質を付加
したものです。で、そういう当時の科学情勢の中で、ド・ブロイがそれまで「粒
子」とされてきたものに逆に「波」の性質を付加した、『物質波』(ド・ブロイ波)
という概念の提案をしました。「量子力学」の幕あきです。
ま、もっとも、ド・ブロイの考えは粒子に付随するパイロット波として捉えてい
たそうですが。
裳華房『量子力学(Ⅰ)』(基礎物理学選書)にはアインシュタイン・ドブロイ
の関係式として下記が最初に示されています。
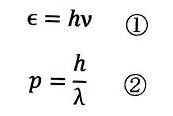
①式は有名なエネルギー量子の式です。②式が「もの」に対して定義された
運動量pと「波」に定義された「波長λ」の関係式というわけです。
これと一般の波動方程式を元に数学的に導かれたのが、量子力学の金字
塔であるシュレディンガー方程式です。色々な表記が出てきます。
「時間を含むシュレディンガー方程式」として下記があります。
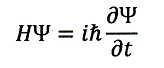
ここで、H;ハミルトニアンで
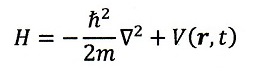
です。右辺第一項は運動エネルギー、第二項はポテンシャルエネルギー
であり、
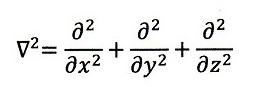
です。また、
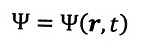
です。Wikipediaなどではなんやらややこしい下式のようなのが示されてい
ます。
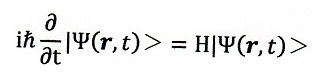
ここで、
Ψ(r,t);状態変数(と称せられている)
|Ψ(r,t)>;ケットベクトル(Diracが発案したもの)
です。
尚、ネットでは
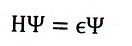
という式を書いているサイトもありますけど、これは
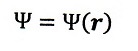
のとき、すなわち「時間を含まないシュレディンガー方程式」ですよね。
シュレディンガーはこれを水素原子に適用して正しさを確信したそうですが
Ψは何かという問題があって最初はなかなか賛同を得られなかったらしい
です。しかし、ハイゼンベルグが粒子に拘って「マトリックス力学」というの
を呈示し、シュレディンガー自身がシュレディンガー方程式と同定できるこ
とを証明したため、よりわかりやすいシュレディンガー方程式が一般的な式
となったようです。「マトリックス力学」に出てくる何かよくわからないベクトル
がこのΨであることがわかったとのことです。
ただし、問題は「ではこのΨって一体全体何なのか?」ということです。
これに一つの回答を与えたのはボルンです。すなわち、
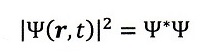
というものを粒子の存在する確率としたわけで、観測される現象をうまく説明
できるのでした(注:これは規格化されて絶対確率化されています)。
結果として、ボーアらからコペンハーゲン解釈
量子力学の状態は、いくつかの異なる状態の重ね合わせで表現され
る。このことを、どちらの状態であるとも言及できないと解釈し、観測す
ると観測値に対応する状態に変化する(波束の収束)(Wikipediaより)
というものが提唱されました。ただし、
確実に言えることは、観測すると波動関数の収縮に相当する現象が
確認できることだけで、それがいつどのようにして起きるのか分から
ない。
収縮に必要な条件を理論的に予測することもできないので、現段階
の科学の枠組みではこれ以上、波動関数の収縮について言及する
ことはできない
としているわけです。要するに、
「なぜか」はわからないが、現象をぴったり説明できるのだから
「なぜか」は考える必要はない
という主張だとされ、それゆえ「プラグマティズム的」という批判もあるので
しょうね。「決定論者」とされたEinsteinは「神はサイを振らない」と反発し、
数々の思考実験でパラドックス論議をボーアに挑みましたが、ボーアは明
確な反論で悉くしりぞけ、結局、Einsteinが最終的決定的だと考えたであ
ろうところの「EPRパラドックス」もアスペの実験でパラドックスにはならない
ことが実証されてしまいました。尚、方程式を導入した張本人のシュレディ
ンガーも反対(真偽のほどはわかりませんが、晩年になって認めたというの
がネットにありましたけどね)して有名な「シュレディンガーの猫」というパラ
ドックスを出しましたけど、こちらは何か曖昧なままうやむやで終わってい
るようですね。
前述の教科書では、「確率の波」という項があり、電子の二重スリット実験
のところで、
両スリットを通った「可能性の波」が干渉して縞を作っている
という説明がされていますが、「確率の波」というのを「可能性の波」などと
言葉の置き換えをしても「わかりにくさ」は変わらないと思うんですが・・・
なぜなら、「可能性の波」などというのは極めて「抽象的」だからです。
ちなみにこの教科書では、
「何とも妙で合点がいかない読者もいると思う。しかしこれが厳然たる
自然現象なのである。」
とし、更には
「古典的に考えると誠に不思議なことであるが、実際にやってみるとそう
なっているから仕方がない」
とまで書かれています。
やっぱり、多くの科学者は無理やり自分に言い聞かせている気がします。
だからこそ、対案として出された「多世界解釈」というのが一定の支持を
得ているようですが、これもあまりにご都合主義的つじつまあわせという
感じが私にはします。ですから、両方ともに賛同できない学者さんも沢山
おられるようですね。
ところで、Wikipediaのコペンハーゲン解釈の項には、ちょっと気になる記
述がさらっとありました。
・確率解釈は、波動関数から粒子の存在確率が求められることを
示しているだけで、決して波動関数が実在する波であることを否定
しているわけではない。
・量子力学の説明では、定義を曖昧にしたまま「観測」という言葉
を安易に使っている事例も多々見受けられる
というものですが・・・
(続く)
目次に戻る
次へ