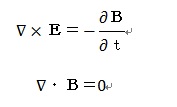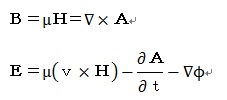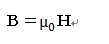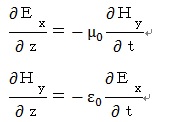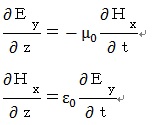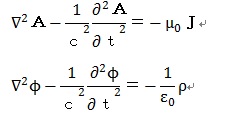Maxwellの方程式を考える(4)電磁波
電磁波の説明に使われるポイントとなる式を現在では『Maxwellの方程式』と
称せられている『Maxwell-Heaviside方程式』(Heavisideが言わば「勝手に」書
き替えたもの)は(3)で示しましたが再掲すると、
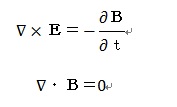
です。一方、対応する『オリジナル式』の方は
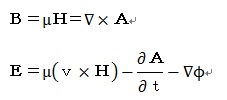
です。
ここでは、オリジナル式についてはおいておいて、現在の教科書で説明されて
いる『Maxwell-Heaviside方程式』の方で電磁波について色々と考えてみます。
大抵は『真空中』で考えて、
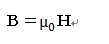
として、上側の式を(x、y、z)成分に分け、更にz方向成分の時間的・空間的
変化はないとして整理した式
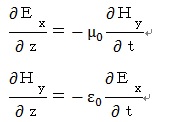
と、
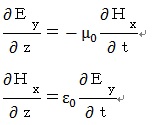
で説明していると思います(私の所有の教科書はこれです)。
恐らく、E⇒H⇒E⇒H・・・などというおかしな説明をされている方達は、これらの
式でEとHが左辺と右辺に分かれて出てきて右辺が時間による偏微分であるこ
とからの発想だと思うのですが、左辺はE,Hそのものではなく、空間的な『勾配』
なんですよね。素人受けはするかもしれませんが、多分、多くの人がこの説明で
納得してしまっているのではないかと懸念してます(以前は私もあまり深く考えず
わかった気になっていました(^_^;))。大変けしからんことです(-_-メ)。
少なくとも私の所有する教科書にはそんなおかしな説明はされていませんから、
啓蒙書かどこかで目にしたものと思うのですが・・・
飛行機の飛ぶ原理をベルヌーイの定理を適用して上面と下面の気流の到着時間
の差でもって説明しているような啓蒙書の過ちと同じ過ちをしているんですよね?
私自身、工学部で電磁気学を学びましたが、授業時間の制約からかMaxwellの方
程式や電磁波について詳細な説明を受けたという記憶がありません。それゆえ、
こういうおかしな説明でなぜか納得してしまっていたというかあまり疑問すら抱かず
にきたというのが事実です(^_^;)。
しかしながら、今更になって教科書をひっくり返して、Maxwellの方程式(実際には
Maxwell-Heviside方程式だったんですが−今までそう言う事実を本当に知りませ
んでした−)と電磁波について調べて考えていると電磁波がどんどんわからなくなっ
てしまいました。特にわかりやすいとして特例で示されている平面波の説明が私に
とっては分からなくなってしまいました。
平面波のときの一般解として、

とされています。これらは勿論、上の方程式を満足しています。
しかしながら、私は奇妙なことに気がついてしまいました。この一般解ってどこに電
磁波の「周波数」が出てくるのかと・・・。
せがれが習った教科書を見せてもらいましたら『単発波』が移動する図がありました。
単発波というのは波長と移動速度はありますけど、周波数などというのはありません
し、波長と移動速度の間に直接の関係などないではないかと・・・
物理で云う『横波』は水面の波のようなものだけを言うのではなく「同じ形を保持しな
がら進行していく」ものというとWikipediaか何かにありましたので、『波』というのを水
面の波のようなものでイメージしてはいけないということだけは理解できましたけど、
では、まず、よく言われている「電磁波の周波数って何なの?」という素朴な疑問が
湧いて来たのです。なぜなら、周波数で「電波」「光」「X線」、「γ線」というような分類
がされているからです。
更に思い違いをしていたことは前述の誤った説明に惑わされて、EとかHという場が
移動していくと思ってしまっていたことです。
で、調べていたら私の所有する教科書に『電磁波の放射』という章がありました。
極めてややこしい数式がずらっと並んでいて目眩がしてしまうくらいでしたが、感性的
に少しわかる気がしてきました。
得た一つの疑問「電磁波の周波数って何?」というのは、ここを見ることで、私的には
電磁波の周波数=電磁波源の周波数
と理解してるのです。そして、前述の周波数で分類している電磁波というのはある方向
の言わば『偏波』されたものだと理解したのです。勿論、これはあくまで私の理解ですが。
更に、filed(場)が移動しているのではなく、電磁波源により周囲の空間が特殊な状態に
なりその状態が拡大していく(偏波にすればある特定方向に伸びて行く)ものだとこれも
あくまで私の理解ですがそういう風に考えています。
その『電磁波の放射』の章になって、ベクトルポテンシャルAとスカラーポテンシャルΦの
波動方程式が突如提示されています。
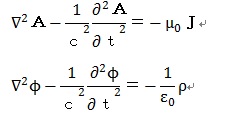
これは非同次波動方程式です(右辺が0ではありません)ので解析的には解けませんが、
定性的には球面波です。これは明らかに、波源から時間的に電磁ポテンシャルという存在
状態が空間的に拡大していく形を示しています。Maxwellのオリジナル式ではE,HがAやΦ
で表されますから、結局、Maxwell-Heaviside式で見ている電磁波におけるE,Hというのは、
ある時間におけるこの球面波の波頭に相当する球面におけるE,Hということになります(
非線形方程式と線形方程式の相違がありますから近似的なものでしょうが)。
恐らく間違いなくMaxwellはこの式で電磁波の存在を予測したと思います。彼は19世紀に既
にベクトルポテンシャルを実在するものと考えてその物理的イメージまで描いていたくらいで
すから。そして、現在、説明に使われている『Maxwell方程式』はMaxwellのオリジナルな式で
なくHevisideが後から勝手に書き換えてしまった式ですから。
ポテンシャルというのはポテンシャルエネルギーとは違いますが、静電ポテンシャルΦは単位
電荷との積、ベクトルポテンシャルAは単位電流ベクトルとのベクトル積でポテンシャルエネル
ギーとなるものですから、前述の球面波というのは波源により生じたあるエネルギーが空間的
に広がって行く(伝達していく)と考えることができこれならイメージしやすい気がしています。
いずれにしろ、『電磁波』というのは必ずエネルギーを生成する『電磁波源』があって、それが周
囲の空間を特別なある励起状態にし、その状態が球面状に拡大していくものであって、周波数
というのはその『電磁波源』が周期的に変化して次から次と球面波が生みだされてくるというこ
とに対応した初期条件ということだと思います。
要するに、『電磁波源』の存在しないような『電磁波』は数式の中だけに存在して実際には
ないということです。
---------------------------------------
私の所有する教科書ではマックスウェルが今の「Maxwell-Heaviside方程式」で上のようにして
平面波を考えて電磁波を見出したような記載がありましたが、「Maxwell-Heaviside方程式」な
んてマックスウェルの没後、かなりたってからHeavisideが書き替えた式で、オリジナル式では
ないことを考えますと、こういう説明はおかしいですよね?マックスウェル本人ではなく後世の
学者が「Maxwell-Heaviside方程式」から考えたことでしょ?きちんと調べて正確に書いてもら
いたいものです。本当にこんな簡単な説明なら当時の学者が理解せずHertzが電磁波を実証
するまで無視されたりしないはずですよね。あとづもでそういう説明されてもなぁ・・・
目次に戻る
次へ