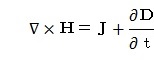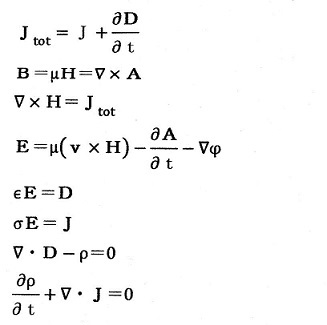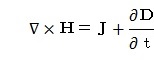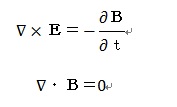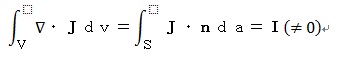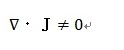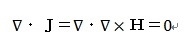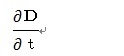Maxwellの方程式を考える(3)オリジナル式は?(改)
(1)で示したMaxwellの『オリジナル』な方程式を成分式を除いた
分だけ下に再掲載しておきます。
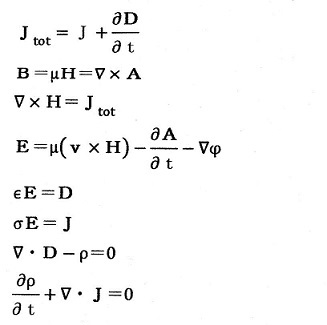
で、このうち、1番目の式と3番目の式を組み合わせた
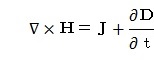 |
① |
と7番目(下から2番目)は今では『Maxwellの方程式』と称せられている4つの
式からなる『Maxwell-Heaviside方程式』に出てくる式です。
残りの二つ、
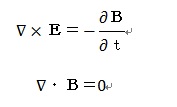
がオリジナルの式と形を異にするものですね。ただし、下の式はオリジナル式の
二番目の式からベクトル公式で容易に出てくるものですので、一番のポイントは
オリジナル式からベクトルポテンシャルAを消去して導出されたことになっている
上側の式ですよね。
ネットにあったのですが、この所謂『Maxwell-Heaviside方程式』が『Maxwellの方
程式』と公式にされた頃、Maxwellは病没されているそうで、Maxwellの感想とか
反論とかは目にできてはいませんが、1860年代に発表してからHerzが電磁波を
発見するまで学界から無視され、挙句の果てにオリジナ式を他人(Heaviside)が
"勝手に"書きかえた式が自分の名前をかたった『Maxwellの方程式』とされてし
まい、折角の自分の構築したオリジナル式をクオータニアンによる拡張したもの
は無視され忘れ去られてしまったことをMaxwell本人はどう感じていたのだろうか
私はすごく気になっているんですがねぇ。
それはとにかくとして、オリジナル式の1番目の式、したがって、Maxwell-Heaviside
方程式のうちの①式はMaxwellの天才的ひらめきによる式なんですよね。
この式でJは『伝導電流』と称されている導体内を流れる電流の密度[A/m^2]を表
すものです。そして、これは上記のオリジナル式の6番目の式で与えられ、σは導
電率です。
電流をIとし、ガウスの発散定理を適用すると、
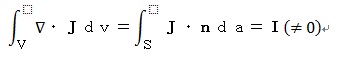
となり、したがって
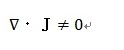
のはずですが、一方、ベクトル公式から
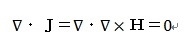
となり矛盾してしまいます。
Maxwellはコンデンサの放電回路から、
回路が開いていても途切れてしまわずソレノイダルな電流を考える
必要がある
と考え、オリジナル式の一番下の8番目の「電荷保存則」とその上の7番目の式
から1番目の式を考え、

という形で矛盾を回避したんですよね。この中の
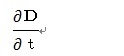
の部分は『変位電流』と呼称されていて、Maxwellは天才的発想で真空中でも存在
すると主張されたようです。
で、ここまでは間違いなくMaxwellのオリジナル式そのものですから、教科書記載の
「Maxwellは」という説明は間違いないでしょう。
しかし、教科書では、次は上記に示したMaxwell-Heaviside方程式を基本にした説明
なのに、そこでも「Maxwellは」という説明が出てきたりします。で、これは、私に言わ
せれば「ほんとうではない」のではと思うのです。現在の教科書は逆方向の説明
(Maxwell-Heaviside方程式⇒冒頭に示したオリジナル式の2番目と4番目の式を導出)
がなされています。そして、そこにはMaxwellの拡張した四元数の考察等は皆無なん
ですよね。決してMaxwellはHeavisideが勝手に書き換えて公式的な式とされてしまった
現在のMaxwell方程式なんぞで電磁波などを考察したわけではないのに、そんなことに
触れておらず、知らないといかにもMaxwellは今のMaxwell-Heaviside方程式からの説明
で電磁波を考えたかのように思ってしまう訳です。恥ずかしながら私はそうでした(^_^;)
-------------------------------------------------------------------
(追記'14/2)
後から気が付いたのですが、ネットで「Maxwellの方程式にはローレンツ力が抜けている」
という指摘を目にしたことを思い出しました。
確かに、現在「Maxwellの方程式」と称せられているもの(実はMaxwell-Heaviside方程式)
にはローレンツ力は入っていませんが、Maxwell自身が作ったオリジナルの方では前述
のように、きちんとそれが入っているんです。自分で気が付いてちゃんと触れて置いて、
そのことをすっかり失念してました(^_^;)。
是非、「Maxwellの方程式にはローレンツ力が抜けている」というご指摘をされている方に
それはMaxwellの責任でなく、書き替えたHeaviside達の責任であることを知っていただき
たいものですね。実は、そういう私も「確かになぁ。なんでだろう?」などと疑問を感じてい
たんですけどね(^_^;)。
後、わざわざ書きませんでしたが、上から6番目の式は『オームの法則』を示しています。
目次に戻る
次へ