「拡張シュレーフリ記号」をベースに勝手に考えた解釈ですが、
似たもので「Conway polyhedron notation」(コンウェイ多面体表記法?)というものがありました。
2016.6.25-2019.3.22
正四面体と半正多面体・カタランの立体の関係
半正多面体・カタランの立体の名称について
大二重斜方二十・十二面体等の塗り分け
ねじれ系の半正多面体等の式
Hemipolyhedronの非一様性
正多面体と半正多面体・カタランの立体は、以下のように全て正四面体からの派生で表す事ができます。

「拡張シュレーフリ記号」をベースに勝手に考えた解釈ですが、
似たもので「Conway polyhedron notation」(コンウェイ多面体表記法?)というものがありました。
2016.6.25-2019.3.22
半正多面体とカタランの立体には、幾つかの別名が存在しています。
しかし、日本語においては今一つ理に合っていない名前が定着してしまっています。
英語では少なくとも英語版Wikipedia上では改善が見られますが、日本語においても対応を望む所です。
| メジャーな呼称 | 推奨する呼称 | 理由 |
|---|---|---|
| 斜方切頂立方八面体 | 切頂立方八面体 | この「斜方」が名前を無駄に難しくしている感があります。この「斜方」は、菱形十二面体や菱形三十面体を意味していますが、同様の理屈では切頂立方体は八面切頂立方体となるもので、大した意味はありません。英語版Wikipediaにおいても、「切頂〜」の方の英訳にあたる「Truncated cuboctahedron」「Truncated icosidodecahedron」が採用されてます。 |
| 斜方切頂二十・十二面体 | 切頂二十・十二面体 | |
| 六方八面体 | 二重二方十二面体 | 上記の「正四面体と半正多面体・カタランの立体の関係」の図やConway polyhedron notationからもわかるように、これらの直属の派生元が「菱形十二面体」「菱形三十面体」だからです。英語版Wikipediaにおいても、「二重二方〜」の方の英訳にあたる「Disdyakis dodecahedron」「Disdyakis triacontahedron」が採用されてます。メジャーな呼び方に倣えば、「八方立方体」「十方二十面体」とも呼ぶ事ができますし、その中であえて「六方〜」という呼称を取るのは偏った見方となってしまいます。個人的には「四方菱形十二面体」「四方菱形三十面体」と呼んだ方が解り易いし良いのではないかと思いますが……。 |
| 六方二十面体 | 二重二方三十面体 | |
| 変形立方体 | 変形立方八面体 | これらについては迷う所もありますが、一様多面体における「大変形二十・十二面体」等に対応する名前は「変形二十・十二面体」等となります。変形立方体等と呼んだ方が解り易い所もありますし、立方八面体→変形立方八面体という変形は特定の条件を満たす多面体にしか使えない点、立方体や正八面体を派生元とした方が理に適ってる部分もありますが、変形立方八面体と斜方立方八面体は、反角柱と角柱のような関係にある点も、一つの手がかりになるかもしれません。 |
| 変形十二面体 | 変形二十・十二面体 |
左から右へ進化するような形になってます。
一応自分で考えたもので、一部を除き、3列目以降はネットでは見かけない塗り方となってます。
| 図形の名前/塗り方 | 星型を塗りつぶす(Wikipediaでも標準となってる一般的な塗り方)
|
星型を中抜きにする(英語版Wikipediaで「neo filling」と呼ばれている塗り方) |
六芒星部分の重なってる三角形なども互いに違う色にする(八芒星部分については、対称性が崩れてしまうため塗分けられない) |
表裏を異なる色にする事を許す事によって、八芒星部分も塗り分ける |
表裏を全て異なる色にする(これにより、従来は「赤の三角形」と「緑の三角形」の2種類が必要だった所が、「表が赤で裏が緑の三角形」の1種類のみで良くなり、一種の単純化が図れる) |
| 大二重斜方二十・十二面体 |  |
 |
 |
 |
 |
| 大二重変形二重斜方十二面体 |  |
 |
 |
 |
 |
| 小反屈変形二十・二十・十二面体 |  |
 |
 |
左に同じ | 左に同じ |
| 小変形二十・二十・十二面体 |  |
 |
 |
左に同じ | 左に同じ |
| 大変形十二・二十・十二面体 |  |
 |
 |
左に同じ |  |
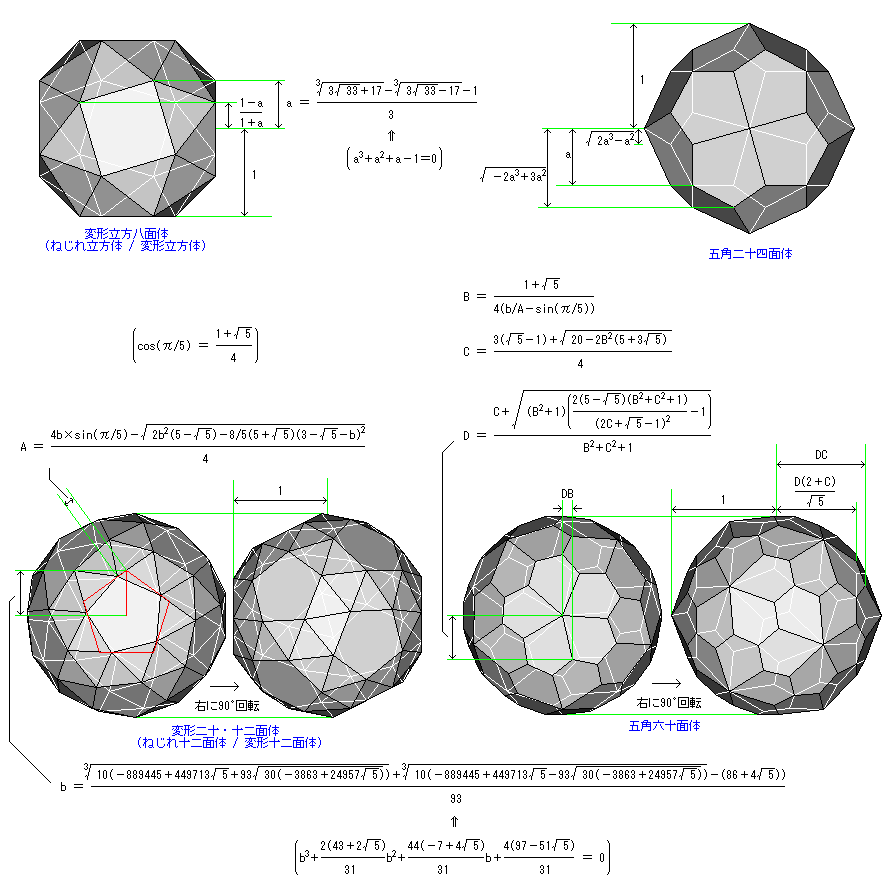
変形立方八面体、変形二十・十二面体、五角二十四面体、五角六十面体の式です。
特に変形二十・十二面体は凄まじく苦労しました。
2016.11.12
一様多面体の内、名称に「半」が入ってる9種、
即ち「四面半六面体」「立方半八面体」「八面半八面体」「小十二面半十二面体」
「小二十面半十二面体」「小十二面半二十面体」「大十二面半二十面体」
「大十二面半十二面体」「大二十面半十二面体」には、「Hemipolyhedron」という
分類名があります。
これらの図形は、辺の周辺が外観の上では合同なので、
日本語版Wikipediaでは(非凸の)準正多面体と説明されていますが、
準正多面体は英語版Wikipediaの定義によれば、頂点形状が(a,b)^nという形で
表現できるものであり、以上の図形はこれには当て嵌まらないため、
本当にそう呼べるかは疑って掛かった方が良いかもしれません。
更にこれらの図形は、一様多面体と言って良いのかどうかも微妙な所があります。
例えば四面半六面体の場合なら、(3, 4, 3/2, 4/3)と(3, 4, 3/2, 4)という、
2種類の異なる頂点によって成り立っている、という見方もできるのです。
この性質は、以下のように、各面を表裏で塗り分ける事で視覚化できます。
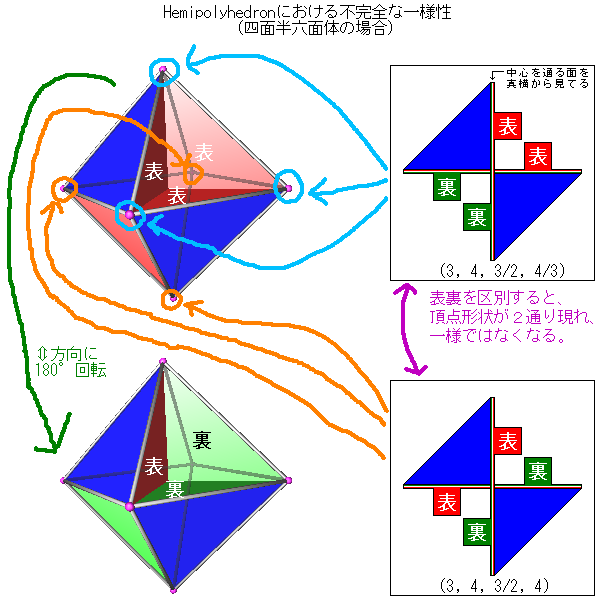
2018.9.20-2021.3.17
図形等に戻る
トップに戻る
その他の一様多面体53種を見る動画@Youtube
半正多面体とカタランの立体による複合多面体を見る動画@Youtube