球面幾何学上の星型

紋章などでお馴染みの五芒星や六芒星などは「星型多角形」と呼ばれています。
五芒星は「正5/2角形」、六芒星は「正6/2角形」に相当しています。
七角形に対して七芒星も存在しますが、七芒星は2種類存在しています。
それをまとめると以下のようになります。


星型多角形の種類はこのように、角の数が２つ増える毎に１つ増えたり、
３角形以上でなければ通常の多角形も構成できなかったりといった、
少々複雑な様相となっています。

一方、球面幾何学上で星型多角形を考えると、以下のような、
１対１の綺麗な表となります。


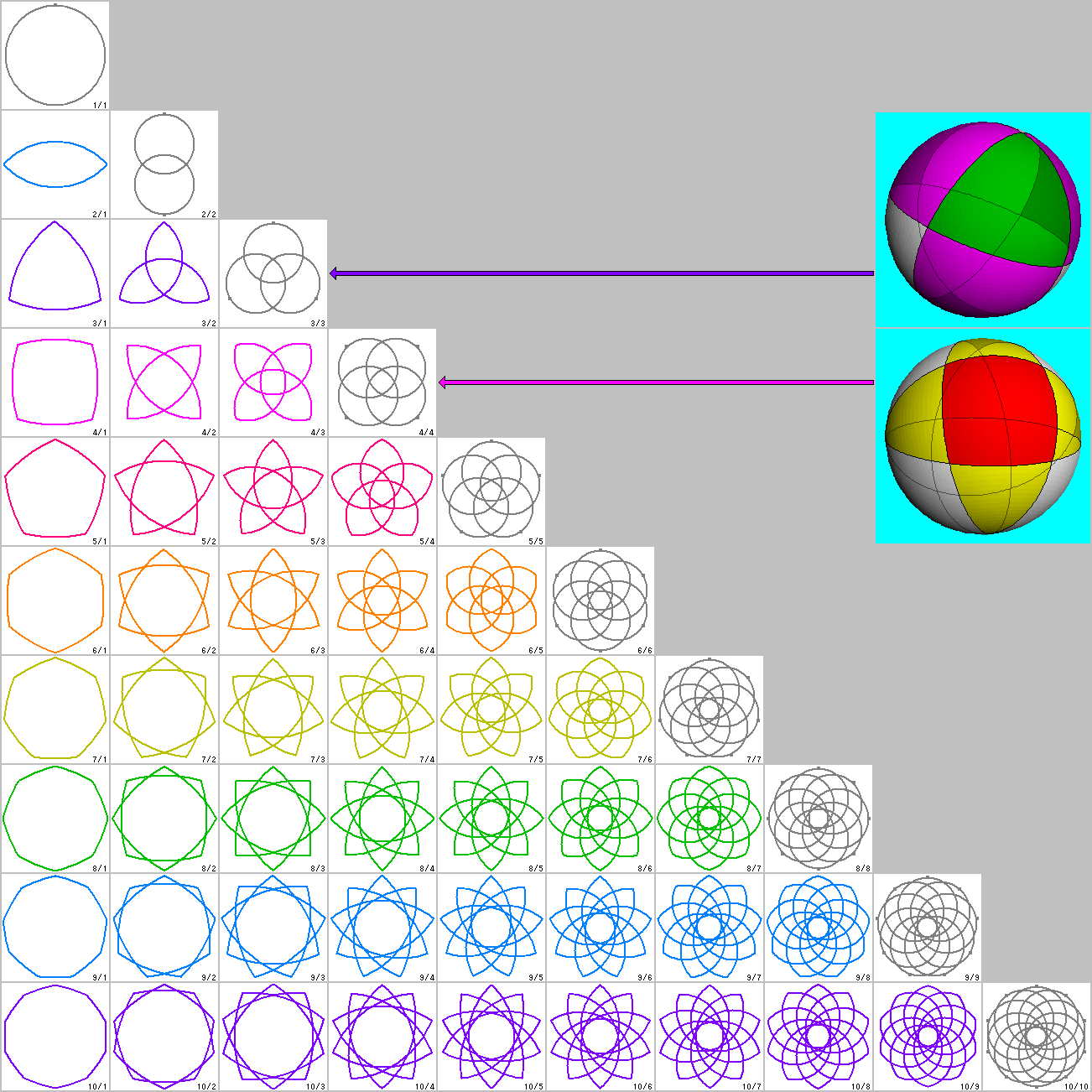
ここで、右上の図が実際に球面上に配した図、後がそれを平面に押し伸ばした表現となっています。
こういう見方は、通常の平面での星型化を考える上でも、役に立つのではないかと思います。

三次元空間上の多面体に対しても「星型多面体」を考える事ができます。
代表的なものとして、以下の星型八面体と星型正多面体シリーズがあります。

星型八面体 （正八面体の唯一の星型）	小星型十二面体 （正十二面体の最初の星型）	大星型十二面体 （正十二面体の最後の星型）
大十二面体 （正十二面体の2番目の星型）	大二十面体 （正二十面体の星型の一種）

正四面体や立方体に対しては星型を作る事はできませんが、
こちらも球面幾何学上（三次元の場合ならば四次元超球面上で考える）においては、
シンプルな形で星型を見出す事ができます。

以下は立方体における例です。

何番目の星型か	形状の概略説明	全体像	一つの面のみを取り出したもの	Stellation diagram（星型化線図？）
0	立方体
1	4つの二角形で構成された四面体3つの複合
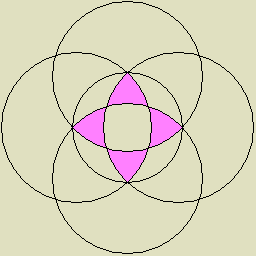2	一角形で構成された二面体3つの複合
3	6つの球面幾何学的な4/3角形で構成された、球面幾何学的な星型正多面体
4	6つの正方形を交差させて構成された球面幾何学的な星型正多面体、あるいは、一角形で構成された二面体12個の複合
5	立方体、あるいは一面体6つの複合

ここで、星型化線図も球面上に描いた方が正確となり、それが次の図となります。


2017.6.4-2021.3.5

図形等に戻る
トップに戻る