角球・一般球

角球

円柱に対して角柱（三角柱や四角柱）、円錐に対して角錐（三角錐や四角錐）が存在しますが、
球に対しても「角球」（三角球や四角球）とでも呼べそうなものが存在しています。
それは例えば以下のようなものです。

三角球	四角球	八角球
通常の球（比較用）

ここで、角球というのはあくまで造語で、正式名称が不明なのでここでは便宜的にこう呼んでいます。
以下は別の表現によるものです。


角柱や角錐は以下のように、星型五角形（五芒星）などに対しても考える事ができますが、
角球についても同じく以下のように、同様のものを考える事ができます。

星型五角錐

星型五角柱

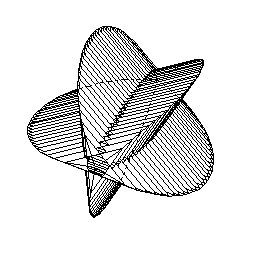星型五角球

更に以下のようなものも考えられます。

円柱、角柱、円錐、角錐、球、角球は、以下のようなイメージでまとめる事ができます。

	○	△	□
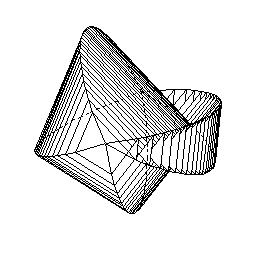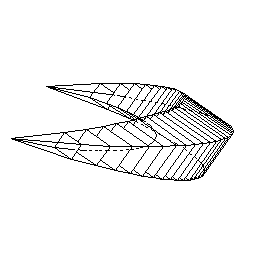○	回転楕円体（特：球）	三角球	四角球
△	円錐	三角錐（特：正四面体）	四角錐
□	円柱	三角柱	四角柱（特：立方体）
◇	双円錐	双三角錐	双四角錐（特：正八面体）

数学的な定義としては、積分で球の体積を求める問題を解いた事のあるかたなら解り易いと思います。
球は、円を平行移動で伸縮させながら積み重ねる事で作る事ができますが、
その時の積み重ねる図形として、円の代わりに多角形を用いる形です。

その定義上、縦に切った断面は楕円（円含む）、または２つの楕円を半々にして滑らかに繋いだ形となります。
加えて、極の部分は滑らかになっています。
滑らかと言っても、厳密には両極の接面が平行になるという事なので、
上図の一番右側のように、横方向に対してならば尖っている事もあります。

なお、四角球はSuperellipsoid（超二次楕円体）なるものの中にも、
円柱や双円錐などと共に見られます。
非常に特徴的な形だと思うので、マイナーなのが不思議です。

この構造はHosohedronに例えられる事があるようですが、
あれは球面幾何学上の多面体という感じっぽいのに対し、
こちらは曲面で構成された立体なので本質的には別物です。
一般的なHosohedronの絵とは面の曲がり方が異なっています。

展開図

角球は意外にも、通常の球と違って、円錐や円柱と同様に、展開図を考える事ができます。
以下はその例となります。

四角球の展開図

三角球の展開図

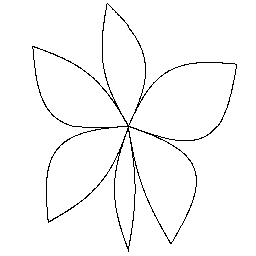何かの角球の展開図

何かしらの角球になる展開図は容易に無数に作成できますが、
角球の概形からその展開図を計算できるのはごく一部で、大抵は非常に難しくなってしまいます。
また、組み立てるのも結構難しいかもしれません。

展開図を考え易いタイプの角球というのは、球に外接するタイプです。
これは円柱を削り出して組み立てる事でも作る事ができますので、
角球の中で最も標準的なタイプと見ても良いかもしれませんが、
いまいち決め手に欠けてます。

体積

角球の体積を考えると、曲面がありますし、横から見たら丸に見えますし、
円柱や円錐はπが入って来ますし、展開図が曲線を含んだ図形になってますので、
πが入って来そうですが、意外にも、πは出現しません。
例えば正方形の四角球ならば、赤道面での一辺の長さをa、赤道面から極までの高さをhと置けば、
体積は、4ha²/3となります。
テキスト上では分数で書くのは難しいのでこういう形にしてますが、
(4/3)ha²という感じです。

後述の一般球の場合でも、赤道面の面積をSと置けば、4hS/3となります。
先の四角球の場合なら、S=a²ですので、同じ式となり、
球の場合なら、S=πr²、h=rですので、4πr³/3となります。
この式は、積分を使って球を求める方法を一般化する事で出て来ます。

円にπが入るなら、球にはπの二乗が入りそうなのに、一つしか無いってのを昔不思議に思ってましたが、
平面図形を球化する段階ではπが入らないので、赤道面の円に含まれるπのみってわけだったのです。
一般には（この辺は他が詳しいと思いますが）、2n-1次元の図形を2n次元の超球化するにはπが入り、
2n次元の図形を2n+1次元の超球化するには入らないです。
つまり、三次元の図形を四次元の超球化する場合にはπが新しく入りますので、
四次元の超球にはπ²が入るわけです。

英名

英語では直訳するとpolygonal sphereとなりそうですが、
その表現は多面体によって球を近似したような図形の意味合いで
用いられてる様子があるので、難しそうです。
polygon based sphereとは呼べるかもしれません。
最終的には、prismやpyramidのように一つの単語に短縮で出来たら良いかもしれません。
「形の似た具体的な物体の名を借りる」という慣習に倣うと、
hozuki(またはhoozuki、hozky)はどうだろうかと思ってます。

多角形回転体と角球

円柱も円錐も双円錐も、多角形回転体の一種として一まとめにできます。
斜柱などもあるので完全に含める事はできませんが、
多角形回転体も斜めにする事はできますので、もう少し定義を広げれば可能そうです。

多角形回転体は全て、横から見れば多角形ですが、上から見れば円です。
角球は逆に、上から見れば多角形、横から見れば円ぽい図形です。
多角形回転体が経度方向に関して丸いのに対し、角球は緯度方向に丸い図形です。
両方の丸さを併せ持つと球や楕円体となります。
どちらも球の半多角形バージョンと言えます。

トーラスに対しても同様に2種の多角形版を考える事ができます。
トーラスは、円柱を円状に丸めた形をしてますが、これに対し、
円柱を多角形状に丸めたものと、角柱を円状に丸めたものが考えられます。
四次元空間図形であるn,m角柱の片方を円柱にしたものは、
この二種が絡み合ったような図形となっています。
それぞれ、円柱多角環、角柱円環とでも呼べそうです。

角柱円環は、回転軸が図系外にある多角形回転体と見る事ができます。
ただ、楕円回転体と言われてトーラスが出て来る事はまずありませんから、
広義の多角形回転体という所でしょうか。
対して円柱多角環は、広義の角球…と取るには少々無理があるかもしれません。
トーラスを球の一種としているようなものです。
円柱→角柱、球→角球という変形は、あらゆる回転体に対して考える事ができます。
角柱、角錐、角球、円柱多角環、この辺を更にまとめた概念が必要になって来るかもしれません。

楕円体

予備知識として、「楕円体（ellipsoid）」というものを簡単に紹介します。
楕円の三次元版といえば、楕円の回転体である「回転楕円体」が有名かもしれませんが、
回転楕円体は、３つの径の内、２つは等しいです。
これに対し、どの径も一致しているとは限らないようなものが楕円体で、以下がその例です。


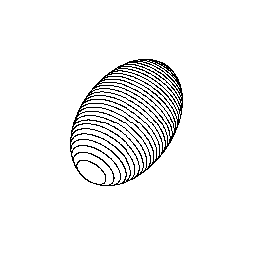
直方体などと比較すると、以下のような対応になっています。

一致しているとは限らない	長方形	直方体	楕円	楕円体
２つは一致している	正方形	正方形を底面とた直柱	円	回転楕円体
３つとも一致している	−	立方体	−	球

長い間、どういう名前なのかを知らず、
便宜的に「三次元版楕円」「楕球」「楕円球」などと呼んでました。

角球の円版

球の角版（球における、円錐・円柱に対する角錐・角柱に相当するもの）として考えた角球ですが、
逆に角球の円版（角球における、角錐・角柱に対する円錐・円柱に相当するもの）を考えると、
球に限定はされず、もう少し幅広い意味を持ちます。

角球には、高さについては任意です。
高さを限定するような決定的な要素が無いためです。
そのためまず、上記の回転楕円体が含まれて来ます。
更に、斜球を考えると、上記の楕円体が含まれて来ます。
逆に、楕円体も必ず斜球の一種となっています。

次に、一般的な角錐や円錐の場合、頂点から底面に降ろした垂線が底面の重心を通らないといけないという条件はありません。
角球の場合も、両極を結ぶ線（以下、「極軸」と仮称）が赤道面の重心を通る必要はありません。
すると、以下のような図形も、角球の円版の一種となって来ます。
ひとまず「歪球」と呼んでます。

浅いずれ球

中ずれ球

深いずれ球

角球の呼び方に従えば、上記は全て「円球」となりそうですが、
通常、円球と言えば球の意味になるようなので、そこが角「球」という呼び方の悩み所です。

一般球

円錐・円柱は底面が円、角錐・角柱は底面が多角形ですが、
これらはどのような平面図形に対しても考える事ができ、
例えばハート錐やハート柱を考える事もできます。
円錐・角錐・ハート錐諸々はまとめて「錐体」、
円柱・角柱・ハート柱諸々はまとめて「柱体」と呼ばれます。

これに対し、球や角球も、任意の平面図形バージョンを考える事ができます。
これをひとまず「一般球」と名付けてます。
以下のような例があります。


錐・錐体という呼び方や、柱・柱体という呼び方に対しては、
球・球体となりますが、これでは真球の意味なってしまうのが悩み所です。
一般球を漢字一字で表し、「角球」と上記の「円球」の「球」をそれと置き換えれば、
すっきりしそうなのですが…。

斜球

斜錐や斜柱に対し、「斜球」と呼べるものも考えられます。
一つ注意点として、「直錐⇔斜錐」と「直柱⇔斜柱」における
「直」「斜」には、少々意味合いの違いが見られます。
その解釈によっては、斜球と呼べるものにも違いが出て来ます。
同様の問題は双錐体の場合にも起こります。

直錐は「頂点から底面に降ろした垂線が底面の重心を通る」という定義をされてますが、
底面の形が複雑な場合は、直錐と斜錐の区別は難しくなり、区別がナンセンスにも思えて来ますし、
底面が無限に広がってて重心が定義でいない場合には、区別は無くなります。

対して直柱と斜柱は、底面の形が複雑でも無限でも、一目瞭然で区別できます。
直柱と斜柱の違いは、底面の形を積み重ねていく方向の違いによるものという考え方ができます。
同じ定義を錐体に対して用いると、直錐と斜錐は区別が付かなくなります。
錐体の場合は伸縮しながら積み重ねる形となってますが、その伸縮の中心となる軸をどこに置くかによって、
例えその軸が底面に対して垂直であろうとも、斜めになるからです。

「全ての切断面の重心を結んだ軸を考える」という方法ならば、
両者の「直」「斜」の意味は一致して来そうですが、それでも重心を定義できない場合は微妙です。

一方、直錐・直柱から斜錐・斜柱を作る操作は、共通の方法で可能です。
全体的に斜めに傾ける方法です。
対応する任意の点同士を結ぶ線を傾けてやる、という言い方もできそうです。
ここでは、この操作でできるものを斜球と呼ぶ事にしようと思います。
なお、通常の球や楕円体の場合、斜球に相当するものは球や楕円体の範疇となって来ます。

角球座標系

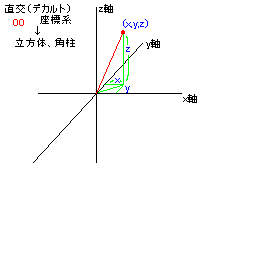直交座標系	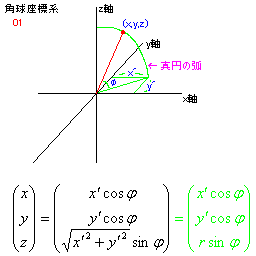角球座標系
円柱座標系（円筒座標系）	球座標系

角球に関連して、三次元の座標系では、ｘｙｚで表す直交座標系、 ｒθｚで表す円柱座標系、ｒθφで表す球座標系の三つが有名です。
でもこれに対し、ｘｙφで表す角球座標系というものを考える事もできます。
直交を００、円柱を１０、球を１１と考えると、角球座標系は０１にちょうど対応しています。
聞いた事が無い所を見ると、実用性は無いのでしょうけど^^;。

以上は厳密には、それぞれ、
（ｘ，ｙ，ｚ）、（ｒ´，θ，ｚ）、（ｘ´，ｙ´，φ）、（ｒ，θ，φ）
で表されてます。
´の記号がｘ´にもｒ´にも付いてますけど、紛らわしい事に、
ｒ´＝√（ｘ^２＋ｙ^２）
ｒ＝√（ｘ^２＋ｙ^２＋ｚ^２）＝√（ｘ´^２＋ｙ´^２）
ですので、注意してください。
これらを組み替える事によって、更に幾つか考える事ができます。
ｘやｒなど、長さを表す要素を固定する事で、以下のように、対応する立体を考える事ができそうです。
角球座標系としては（ｘ，ｙ，φ）型も考えられそうですが、 この考え方により、開角柱座標系と見なせそうです（「開」は、無限遠まで続くけど、遠くなるほど希薄になる、というイメージから）。
尤も、角球座標系も、ちゃんとした角球にはならないですが^^;。
また、開角柱座標には死角があるので、やはり上記で示した角球座標の方が、より標準のものとして扱えそうです。
（ｒ´，θ，φ）⇒開円柱（ｚ軸上不定）
（ｘ，ｙ，φ）⇒開角柱（ｚ軸上不定）
（ｒ，θ，ｚ）⇒球台
（ｘ´，ｙ´，ｚ）⇒角球台
（ｒ，ｒ´，θ）⇒円柱＋球（ｚ符号不定）
（ｒ，ｘ，ｙ）⇒角柱＋球（ｚ符号不定）
（θ，φ，ｚ）⇒開板（ｘｙ平面上不定）

2006.1.15-2021.3.4

図形等に戻る
トップに戻る
角球の紹介@Youtube